Постоянная Апери

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
(перенаправлено с «Константа Апери»)
Иррациональные числа
ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — eπ и π

Постоя́нная Апери́  (англ. Apéry's constant, фр. Constante d'Apéry) — вещественное число, обозначаемое [math]\displaystyle{ \zeta(3) }[/math] (иногда [math]\displaystyle{ \zeta_3 }[/math]), которое равно сумме обратных к кубам целых положительных чисел и, следовательно, является частным значением дзета-функции Римана:

[math]\displaystyle{ \zeta(3)=\sum_{k=1}^\infty\frac{1}{k^3}=\frac{1}{1^3}+\frac{1}{2^3} + \frac{1}{3^3} +\frac{1}{4^3} + \dots }[/math].

Численное значение постоянной выражается бесконечной непериодической десятичной дробью[1][2]:

[math]\displaystyle{ \displaystyle\zeta(3) = }[/math] 1,202 056 903 159 594 285 399 738 161 511 449 990 764 986 292 340 498 881 792 271 555 3…

Названа в честь Роже Апери, доказавшего в 1978 году, что [math]\displaystyle{ \zeta(3) }[/math] является иррациональным числом (теорема Апери[англ.][3][4]). Изначальное доказательство носило сложный технический характер, позднее найден простой вариант доказательства с использованием многочленов Лежандра. Неизвестно, является ли постоянная Апери трансцендентным числом.

Эта постоянная давно привлекала интерес математиков — ещё в 1735 году Леонард Эйлер[5][6] вычислил её с точностью до 16 значащих цифр (1,202056903159594).

Приложения в математике и физике

Двухпетлевая диаграмма Фейнмана, результат для которой содержит [math]\displaystyle{ \zeta(3) }[/math]

В математике постоянная Апери встречается во многих приложениях. В частности, величина, обратная [math]\displaystyle{ \zeta(3) }[/math], даёт вероятность того, что любые три случайным образом выбранных положительных целых числа будут взаимно просты — в том смысле, что при [math]\displaystyle{ N\to\infty }[/math] вероятность того, что три положительных целых числа, меньших, чем [math]\displaystyle{ {\textstyle{N}} }[/math] (и выбранных случайным образом) будут взаимно простыми, стремится к [math]\displaystyle{ 1/\zeta(3) }[/math].

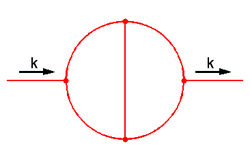
Постоянная Апери естественным образом возникает в ряде проблем физики, включая поправки второго (и выше) порядков к аномальному магнитному моменту электрона в квантовой электродинамике. Например, результат для двухпетлевой диаграммы Фейнмана, изображённой на рисунке, даёт [math]\displaystyle{ 6\zeta(3) }[/math] (здесь предполагается 4-мерное интегрирование по импульсам внутренних петель, содержащих только безмассовые виртуальные частицы, а также соответствующая нормировка, включая степень импульса внешней частицы [math]\displaystyle{ k }[/math]). Другой пример — двумерная модель Дебая.

Связь с другими функциями

Постоянная Апери связана с частным значением полигамма-функции второго порядка:

[math]\displaystyle{ \zeta(3) = -\tfrac{1}{2} \, \psi^{(2)}(1) }[/math]

и появляется в разложении гамма-функции в ряд Тейлора:

[math]\displaystyle{ \Gamma(1+\varepsilon) = e^{-\gamma\varepsilon} \left[ 1 + \tfrac{1}{12}\pi^2 \varepsilon^2 - \tfrac{1}{3} \zeta(3) \varepsilon^3 +O(\varepsilon^4) \right] }[/math],

где в виде [math]\displaystyle{ e^{-\gamma\varepsilon} }[/math] факторизуются вклады, содержащие постоянную Эйлера — Маскерони [math]\displaystyle{ {\textstyle{\gamma}} }[/math].

Постоянная Апери также связана со значениями трилогарифма [math]\displaystyle{ \mathrm{Li}_3(z) }[/math] (частный случай полилогарифма [math]\displaystyle{ \mathrm{Li}_n(z) }[/math]):

[math]\displaystyle{ \mathrm{Li}_3(1) = \zeta(3) }[/math],
[math]\displaystyle{ \mathrm{Li}_3\left(\tfrac12\right) = \tfrac16 (\ln 2)^3 - \tfrac1{12} \pi^2 \ln 2 + \tfrac78 \,\zeta(3) }[/math].

Представления в виде рядов

Некоторые другие ряды, члены которых обратны к кубам натуральных чисел, также выражаются через постоянную Апери:

[math]\displaystyle{ \zeta(3) = \tfrac{4}{3} \sum_{k=1}^\infty \frac{(-1)^{k-1}}{k^3} = \tfrac{4}{3} \left( 1-\frac{1}{2^3} + \frac{1}{3^3} -\frac{1}{4^3} + \cdots \right) }[/math],
[math]\displaystyle{ \zeta(3) = \tfrac{8}{7} \sum_{k=0}^\infty \frac{1}{(2k+1)^3} = \tfrac{8}{7} \left( 1+\frac{1}{3^3} + \frac{1}{5^3} +\frac{1}{7^3} + \cdots \right) }[/math].

Другие известные результаты — сумма ряда, содержащего гармонические числа [math]\displaystyle{ {\textstyle{H_k}} }[/math]:

[math]\displaystyle{ \zeta(3) = \tfrac{1}{2} \sum_{k=1}^\infty \frac{H_k}{k^2} }[/math],

а также двукратная сумма:

[math]\displaystyle{ \zeta(3) = \tfrac{1}{2} \sum_{j=1}^\infty \sum_{k=1}^\infty \frac{1}{jk(j+k)} }[/math].

Для доказательства иррациональности [math]\displaystyle{ \zeta(3) }[/math] Роже Апери[3] пользовался представлением:

[math]\displaystyle{ \zeta(3) = \tfrac{5}{2} \sum_{k=1}^\infty (-1)^{k-1} \frac{(k!)^2}{k^3 (2k)!} = \tfrac{5}{2} \sum_{k=1}^\infty \frac{(-1)^{k-1}}{k^3 \binom{2k}{k}} }[/math],

где [math]\displaystyle{ {\textstyle{\binom{2k}{k}}=\frac{(2k)!}{k!^2}} }[/math] — биномиальный коэффициент.

В 1773 году Леонард Эйлер[7] привёл представление в виде ряда[8] (которое впоследствии было несколько раз заново открыто в других работах):

[math]\displaystyle{ \zeta(3)=\tfrac{1}{7} \pi^2 \left[ 1-4\sum_{k=1}^\infty \frac {\zeta (2k)} {(2k+1)(2k+2) 2^{2k}} \right] }[/math],

в котором значения дзета-функции Римана чётных аргументов могут быть представлены как [math]\displaystyle{ {\textstyle{\zeta(2k) = (-1)^{k+1} (2\pi)^{2k} B_{2k}/(2(2k)!)}} }[/math], где [math]\displaystyle{ {\textstyle{B_{2k}}} }[/math] — числа Бернулли.

Рамануджан дал несколько представлений в виде рядов, которые замечательны тем, что они обеспечивают несколько новых значащих цифр на каждой итерации. Они включают в себя[9]:

[math]\displaystyle{ \zeta(3)=\tfrac{7}{180}\pi^3 -2 \sum_{k=1}^\infty \frac{1}{k^3 (e^{2\pi k} -1)} }[/math]

Саймон Плафф[англ.] получил ряды другого типа[10]

[math]\displaystyle{ \zeta(3)= 14 \sum_{k=1}^\infty \frac{1}{k^3 \sinh(\pi k)} -\tfrac{11}{2} \sum_{k=1}^\infty \frac{1}{k^3 (e^{2\pi k} -1)} -\tfrac{7}{2} \sum_{k=1}^\infty \frac{1}{k^3 (e^{2\pi k} +1)} \; , }[/math]

а также аналогичные представления для других постоянных [math]\displaystyle{ \zeta(2n+1) }[/math].

Были также получены другие представления в виде рядов, включая:

[math]\displaystyle{ \zeta(3) = \tfrac{1}{4} \sum_{k=1}^\infty (-1)^{k-1} \frac{(56k^2-32k+5)(k-1)!^3}{(2k-1)^2(3k)!} }[/math]
[math]\displaystyle{ \zeta(3)=\tfrac{8}{7}-\tfrac{8}{7}\sum_{k=1}^\infty \frac{{\left( -1 \right) }^k\,2^{-5 + 12\,k}\,k\, \left( -3 + 9\,k + 148\,k^2 - 432\,k^3 - 2688\,k^4 + 7168\,k^5 \right) \, {k!}^3\,{\left( -1 + 2\,k \right) !}^6}{{\left( -1 + 2\,k \right) }^3\, \left( 3\,k \right) !\,{\left( 1 + 4\,k \right) !}^3} }[/math]
[math]\displaystyle{ \zeta(3) = \tfrac{1}{64} \sum_{k=0}^\infty (-1)^k \frac{(205k^2 + 250k + 77)\cdot k!^{10}}{(2k+1)!^5} }[/math]
[math]\displaystyle{ \zeta(3) = \tfrac{1}{24} \sum_{k=0}^\infty (-1)^k \frac{((2k+1)!(2k)!k!)^3 (126392k^5 + 412708k^4 + 531578k^3 + 336367k^2 + 104000k + 12463)}{(3k+2)!\cdot (4k+3)!^3} }[/math]

Некоторые из этих представлений были использованы для вычисления постоянной Апери со многими миллионами значащих цифр.

В 1998 году получено представление в виде ряда[11], которое даёт возможность вычислить произвольный бит постоянной Апери.

Представления в виде интегралов

Существует также большое количество различных интегральных представлений для постоянной Апери, начиная от тривиальных формул типа

[math]\displaystyle{ \zeta(3) =\frac{1}{2}\int\limits_0^\infty \! \frac{x^2}{e^x-1}\, dx =\frac{2}{3}\int\limits_0^\infty \! \frac{x^2}{e^x+1}\, dx }[/math]

или

[math]\displaystyle{ \zeta(3) =\int\limits_0^1 \! \frac{\ln(x)\ln(1-x)}{x}\, dx }[/math]

следующих из простейших интегральных определений дзета-функции Римана[12], до достаточно сложных, таких, как

[math]\displaystyle{ \zeta(3)=\pi\!\!\int\limits_{0}^{\infty} \! \frac{\cos(2\,\mathrm{arctg}\,x)}{\left(x^2+1\right)\big[\mathrm{ch}\big(\frac{1}{2}\pi x\big)\big]^2}\, dx\qquad }[/math] (Иоган Йенсен[13]),
[math]\displaystyle{ \zeta(3) =-\frac{1}{2}\int\limits_0^1 \!\!\int\limits_0^1 \frac{\ln(xy)}{\,1-xy\,}\, dx \, dy\qquad }[/math] (Фритс Бёкерс[англ.][14]),
[math]\displaystyle{ \zeta(3) =\,\frac{8\pi^2}{7}\!\!\int\limits_0^1 \! \frac{x\left(x^4-4x^2+1\right)\ln\ln\frac{1}{x}}{\,(1+x^2)^4\,}\, dx \qquad }[/math] (Ярослав Благушин[15]).

Цепные дроби

Цепная дробь для константы Апери (последовательность A013631 в OEIS) выглядит следующим образом:

[math]\displaystyle{ \zeta(3) = [1; 4, 1, 18, 1, 1, 1, 4, 1, 9, 9, 2, 1, 1, 1, 2, 7, 1, 1, 7, 11, 1, 1, 1,\cdots] = }[/math]
[math]\displaystyle{ = 1+\cfrac{1}{4+\cfrac{1}{1+\cfrac{1}{18+\cfrac{1}{1+\ldots}}}}\; }[/math]

Первую обобщённую цепную дробь для константы Апери, имеющую закономерность, открыли независимо Стилтьес и Рамануджан:

[math]\displaystyle{ \zeta(3) = 1 + \cfrac{1}{4+\cfrac{1^3}{1+\cfrac{1^3}{12+\cfrac{2^3}{1 + \cfrac{2^3}{20+\cfrac{3^3}{1+\cfrac{3^3}{28+\cfrac{\dots}{\dots+\cfrac{n^3}{1+\cfrac{n^3}{4(2n+1)+\dots}}}}}}}}}} }[/math]

Она может быть преобразована к виду:

[math]\displaystyle{ \zeta(3) = 1 + \cfrac{1}{5-\cfrac{1^6}{21-\cfrac{2^6}{55-\cfrac{3^6}{119-\cfrac{4^6}{225-\cfrac{\dots}{\dots+\cfrac{n^6}{(2n^3+3n^2+11n+5)+\dots}}}}}}} }[/math]

Апери смог ускорить сходимость цепной дроби для константы:

[math]\displaystyle{ \zeta(3) = \frac{6}{5}-\cfrac{1^6}{117 - \cfrac{2^6}{535-\cfrac{3^6}{1436-\cfrac{4^6}{3105-\cfrac{\dots}{\dots+\cfrac{n^6}{(34n^3+51n^2+27n+5)+\dots}}}}}} }[/math][16][17]

Вычисление десятичных цифр

Число известных значащих цифр постоянной Апери [math]\displaystyle{ \zeta(3) }[/math] значительно выросло за последние десятилетия благодаря как увеличению компьютерных мощностей, так и улучшению алгоритмов[18].

Число известных значащих цифр постоянной Апери [math]\displaystyle{ \zeta(3) }[/math]
Дата Количество значащих цифр Авторы вычисления
1735 16 Леонард Эйлер[5][6]
1887 32 Томас Иоаннес Стилтьес
1996 520 000 Greg J. Fee & Simon Plouffe
1997 1 000 000 Bruno Haible & Thomas Papanikolaou
1997, май 10 536 006 Patrick Demichel
1998, февраль 14 000 074 Sebastian Wedeniwski
1998, март 32 000 213 Sebastian Wedeniwski
1998, июль 64 000 091 Sebastian Wedeniwski
1998, декабрь 128 000 026 Sebastian Wedeniwski[19]
2001, сентябрь 200 001 000 Shigeru Kondo & Xavier Gourdon
2002, февраль 600 001 000 Shigeru Kondo & Xavier Gourdon
2003, февраль 1 000 000 000 Patrick Demichel & Xavier Gourdon
2006, апрель 10 000 000 000 Shigeru Kondo & Steve Pagliarulo[20]
2009, январь 15 510 000 000 Alexander J. Yee & Raymond Chan[21]
2009, март 31 026 000 000 Alexander J. Yee & Raymond Chan[21]
2010, сентябрь 100 000 001 000 Alexander J. Yee[22]
2013, сентябрь 200 000 001 000 Robert J. Setti[22]
2015, август 250 000 000 000 Ron Watkins[22]
2015, декабрь 400 000 000 000 Dipanjan Nag[22]
2017, август 500 000 000 000 Ron Watkins[22]
2019, май 1 000 000 000 000 Ian Cutress[22]
2020, июль 1 200 000 000 000 Seungmin Kim[23]

Другие значения дзета-функции в нечётных точках

Существует много исследований, посвящённых другим значениям дзета-функции Римана в нечётных точках [math]\displaystyle{ \zeta(2n+1) }[/math] при [math]\displaystyle{ n\gt 1 }[/math]. В частности, в работах Вадима Зудилина[англ.] и Тангая Ривоаля показано, что иррациональными является бесконечное множество чисел [math]\displaystyle{ \zeta(2n+1) }[/math][24], а также что по крайней мере одно из чисел [math]\displaystyle{ \zeta(5) }[/math], [math]\displaystyle{ \zeta(7) }[/math], [math]\displaystyle{ \zeta(9) }[/math], или [math]\displaystyle{ \zeta(11) }[/math] является иррациональным[25].

Примечания

  1. ↑ Simon Plouffe, Zeta(3) or Apery constant to 2000 places, <http://www.worldwideschool.org/library/books/sci/math/MiscellaneousMathematicalConstants/chap97.html>. Проверено 8 февраля 2011.  Архивная копия от 5 февраля 2008 на Wayback Machine
  2. ↑ последовательность A002117 в OEIS
  3. ↑ 3,0 3,1 Roger Apéry (1979), Irrationalité de ζ(2) et ζ(3), Astérisque Т. 61: 11–13 
  4. ↑ A. van der Poorten (1979), A proof that Euler missed... Apéry’s proof of the irrationality of ζ(3). An informal report, The Mathematical Intelligencer Т. 1: 195–203, doi:10.1007/BF03028234, <http://www.maths.mq.edu.au/~alf/45.pdf>. Проверено 8 февраля 2011.  Архивная копия от 6 июля 2011 на Wayback Machine
  5. ↑ 5,0 5,1 Leonhard Euler (1741), Inventio summae cuiusque seriei ex dato termino generali (13 октября 1735), Commentarii academiae scientiarum Petropolitanae Т. 8: 173–204, <http://math.dartmouth.edu/~euler/docs/originals/E047.pdf>. Проверено 9 февраля 2011.  Архивная копия от 23 июня 2011 на Wayback Machine
  6. ↑ 6,0 6,1 Leonhard Euler (translation by Jordan Bell, 2008), Finding the sum of any series from a given general term, arXiv:0806.4096, <http://arxiv.org/PS_cache/arxiv/pdf/0806/0806.4096v1.pdf>. Проверено 9 февраля 2011.  Архивная копия от 28 июня 2021 на Wayback Machine
  7. ↑ Leonhard Euler (1773), Exercitationes analyticae, Novi Commentarii academiae scientiarum Petropolitanae Т. 17: 173–204, <http://math.dartmouth.edu/~euler/docs/originals/E432.pdf>. Проверено 8 февраля 2011.  Архивная копия от 17 сентября 2006 на Wayback Machine
  8. ↑ H. M. Srivastava (2000), Some Families of Rapidly Convergent Series Representations for the Zeta Functions, Taiwanese Journal of Mathematics Т. 4 (4): 569–598, ISSN 1027-5487, <http://www.math.nthu.edu.tw/~tjm/abstract/0012/tjm0012_3.pdf>. Проверено 8 февраля 2011.  Архивная копия от 19 июля 2011 на Wayback Machine
  9. ↑ Bruce C. Berndt (1989), Ramanujan's notebooks, Part II, Springer-Verlag, ISBN 978-0-387-96794-3, <https://www.springer.com/mathematics/numbers/book/978-0-387-96794-3>. Проверено 8 февраля 2011.  Архивная копия от 17 августа 2010 на Wayback Machine
  10. ↑ Simon Plouffe (1998), Identities inspired from Ramanujan Notebooks II, <http://www.lacim.uqam.ca/~plouffe/identities.html>. Проверено 8 февраля 2011.  Архивная копия от 30 января 2009 на Wayback Machine
  11. ↑ D. J. Broadhurst (1998), Polylogarithmic ladders, hypergeometric series and the ten millionth digits of ζ(3) and ζ(5), arXiv (math.CA/9803067), <http://arxiv.org/abs/math.CA/9803067>. Проверено 8 февраля 2011.  Архивная копия от 13 июля 2019 на Wayback Machine
  12. ↑ Г. М. Фихтенгольц. Курс дифференциального и интегрального исчисления (7-ое изд.), с. 769. Наука, Москва, 1969
  13. ↑ Johan Ludwig William Valdemar Jensen. Note numéro 245. Deuxième réponse. Remarques relatives aux réponses du MM. Franel et Kluyver. L’Intermédiaire des mathématiciens, tome II, pp. 346—347, 1895.
  14. ↑ F. Beukers A Note on the Irrationality of ζ(2) and ζ(3). Bull. London Math. Soc. 11, pp. 268—272, 1979.
  15. ↑ Iaroslav V. Blagouchine Rediscovery of Malmsten’s integrals, their evaluation by contour integration methods and some related results. The Ramanujan Journal, vol. 35, no. 1, pp. 21-110, 2014. Архивная копия от 12 декабря 2017 на Wayback Machine PDF Архивная копия от 7 мая 2021 на Wayback Machine
  16. ↑ Steven R. Finch Mathematical Constants 1.6.6. Дата обращения: 10 августа 2020. Архивировано 28 ноября 2020 года.
  17. ↑ van der Poorten, Alfred (1979), A proof that Euler missed ... Apéry’s proof of the irrationality of ζ(3), The Mathematical Intelligencer Т. 1 (4): 195–203, doi:10.1007/BF03028234, <https://web.archive.org/web/20110706114957/http://www.maths.mq.edu.au/~alf/45.pdf> 
  18. ↑ X. Gourdon & P. Sebah, Constants and Records of Computation, numbers.computation.free.fr, <http://numbers.computation.free.fr/Constants/constants.html>. Проверено 8 февраля 2011.  Архивная копия от 15 января 2011 на Wayback Machine
  19. ↑ Sebastian Wedeniwski (2001), The Value of Zeta(3) to 1,000,000 places, Project Gutenberg 
  20. ↑ Xavier Gourdon & Pascal Sebah (2003), The Apéry's constant: ζ(3), <http://numbers.computation.free.fr/Constants/Zeta3/zeta3.html>. Проверено 8 февраля 2011.  Архивная копия от 13 ноября 2008 на Wayback Machine
  21. ↑ 21,0 21,1 Alexander J. Yee & Raymond Chan (2009), Large Computations, <http://www.numberworld.org/nagisa_runs/computations.html>. Проверено 8 февраля 2011.  Архивная копия от 9 декабря 2009 на Wayback Machine
  22. ↑ 22,0 22,1 22,2 22,3 22,4 22,5 Alexander J. Yee (2015), Zeta(3) — Apery's Constant, <http://www.numberworld.org/digits/Zeta%283%29/>. Проверено 24 ноября 2018.  Архивная копия от 18 ноября 2018 на Wayback Machine
  23. ↑ Apéry’s Constant | Polymath Collector. Дата обращения: 27 февраля 2021. Архивировано 17 октября 2020 года.
  24. ↑ T. Rivoal (2000), La fonction zeta de Riemann prend une infnité de valuers irrationnelles aux entiers impairs, Comptes Rendus Acad. Sci. Paris Sér. I Math. Т. 331: 267–270 
  25. ↑ В. В. Зудилин. Одно из чисел ζ(5), ζ(7), ζ(9), ζ(11) иррационально // УМН. — 2001. — Т. 56, вып. 4(340). — С. 149–150.

Ссылки

Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Постоянная_Апери&oldid=5799890