Десятичная дробь

Примеры конечных десятичных дробей

Десяти́чная дробь — разновидность дроби, которая представляет собой способ представления действительных чисел в виде

[math]\displaystyle{ \pm d_m \ldots d_1 d_0{,} d_{-1} d_{-2} \ldots }[/math]

где

[math]\displaystyle{ \pm }[/math] — знак дроби: либо [math]\displaystyle{ + }[/math], либо [math]\displaystyle{ - }[/math],

[math]\displaystyle{ , }[/math] — десятичная запятая, служащая разделителем между целой и дробной частью числа (стандарт стран СНГ),

[math]\displaystyle{ d_k }[/math] — десятичные цифры. Причём последовательность цифр до запятой (слева от неё) конечна (как минимум одна цифра), а после запятой (справа от неё) — может быть как конечной (в частности, цифры после запятой могут вообще отсутствовать), так и бесконечной.

Примеры:

• [math]\displaystyle{ 123{,}45 }[/math] (конечная десятичная дробь)
• Представление числа [math]\displaystyle{ \pi }[/math] в виде бесконечной десятичной дроби: [math]\displaystyle{ 3{,}1415926535897... }[/math]

Значением десятичной дроби [math]\displaystyle{ \pm d_m \ldots d_1 d_0, d_{-1} d_{-2} \ldots }[/math] является действительное число

[math]\displaystyle{ \pm \left (d_m \cdot 10^m + \ldots + d_1 \cdot 10^1 + d_0 \cdot 10^0 + d_{-1} \cdot 10^{-1} + d_{-2} \cdot 10^{-2} + \ldots \right ), }[/math]

равное сумме конечного или бесконечного числа слагаемых.

Представление действительных чисел с помощью десятичных дробей является обобщением записи целых чисел в десятичной системе счисления. В представлении целого числа в виде десятичной дроби отсутствуют цифры после запятой, и таким образом, это представление имеет вид

[math]\displaystyle{ \pm d_m \ldots d_1 d_0, }[/math]

что совпадает с записью этого числа в десятичной системе счисления.

Конечные и бесконечные десятичные дроби

Конечные дроби

Десятичная дробь называется конечной, если она содержит конечное число цифр после запятой (в частности, ни одного), то есть имеет вид

[math]\displaystyle{ \pm a_0{,}a_1 a_2 \ldots a_n }[/math]

В соответствии с определением эта дробь представляет число

[math]\displaystyle{ \pm \sum_{k=0}^{n} a_k \cdot 10^{-k} }[/math]

Легко видеть, что это число можно представить в виде обыкновенной дроби вида [math]\displaystyle{ p/10^{s} }[/math], знаменатель которой является степенью десятки. Обратно, любое число вида [math]\displaystyle{ p/10^{s} }[/math], где [math]\displaystyle{ p }[/math] — целое, а [math]\displaystyle{ s }[/math] — целое неотрицательное, можно записать в виде конечной десятичной дроби.

Если обыкновенную дробь [math]\displaystyle{ p/10^{s} }[/math] привести к несократимому виду, её знаменатель будет иметь вид [math]\displaystyle{ 2^{m} 5^{n} }[/math]. Таким образом, имеет место следующая теорема о представимости действительных чисел в виде конечных десятичных дробей.

Теорема. Действительное число представимо в виде конечной десятичной дроби тогда и только тогда, когда оно является рациональным и при записи его несократимой дробью [math]\displaystyle{ p/q }[/math] знаменатель [math]\displaystyle{ q }[/math] не имеет простых делителей, отличных от [math]\displaystyle{ 2 }[/math] и [math]\displaystyle{ 5 }[/math].

Бесконечные дроби

Бесконечная десятичная дробь

[math]\displaystyle{ \pm a_0{,}a_1 a_2 \ldots }[/math]

представляет, согласно определению, действительное число

[math]\displaystyle{ \pm \sum_{k=0}^{\infty} a_k \cdot 10^{-k} }[/math]

Этот ряд сходится, каковы бы ни были целое неотрицательное [math]\displaystyle{ a_0 }[/math] и десятичные цифры [math]\displaystyle{ a_1, a_2, \ldots }[/math]. Это предложение вытекает из того факта, что последовательность его частичных сумм (если отбросить знак дроби) ограничена сверху числом [math]\displaystyle{ a_0+1 }[/math] (см. критерий сходимости знакоположительных рядов).

Представление действительных чисел десятичными дробями

Таким образом, всякая конечная или бесконечная десятичная дробь представляет некоторое вполне определённое действительное число. Остаются следующие вопросы:

1. Всякое ли действительное число может быть представлено в виде десятичной дроби?
2. Единственно ли такое представление?
3. Каков алгоритм разложения числа в десятичную дробь?

Эти вопросы освещаются ниже.

Алгоритм разложения числа в десятичную дробь

Ниже описывается алгоритм построения по произвольному действительному числу [math]\displaystyle{ \alpha }[/math] десятичной дроби, которая является его представлением.

Рассмотрим вначале случай [math]\displaystyle{ \alpha \geqslant 0 }[/math]. Разделим всю числовую прямую целочисленными точками на отрезки единичной длины. Рассмотрим тот отрезок [math]\displaystyle{ I_0 }[/math], который содержит точку [math]\displaystyle{ \alpha }[/math]; в частном случае, когда точка [math]\displaystyle{ \alpha }[/math] является концом двух соседних отрезков, в качестве [math]\displaystyle{ I_0 }[/math] выберем правый отрезок.

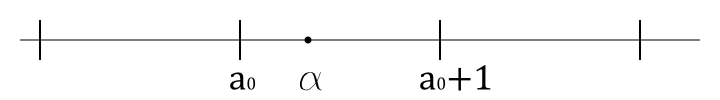
Если обозначить целое неотрицательное число, являющееся левым концом отрезка [math]\displaystyle{ I_0 }[/math], через [math]\displaystyle{ a_0 }[/math], то можно записать:

[math]\displaystyle{ I_0 = [a_0 \, ; \, a_0 + 1] }[/math]

На следующем шаге разделим отрезок [math]\displaystyle{ I_0 }[/math] на десять равных частей точками

[math]\displaystyle{ a_0 + b/10, \; b = 1, \ldots, 9 }[/math]

и рассмотрим тот из отрезков длины [math]\displaystyle{ 1/10 }[/math], на котором лежит точка [math]\displaystyle{ \alpha }[/math]; в случае когда эта точка является концом двух соседних отрезков, из этих двух отрезков опять выберем правый.

Обозначим этот отрезок [math]\displaystyle{ I_1 }[/math]. Он имеет вид:

[math]\displaystyle{ I_1 = \left [ a_0 + \frac{a_1}{10} \, ; \, a_0 + \frac{a_1 + 1}{10} \right ] }[/math]

Будем продолжать аналогичным образом процесс измельчения числовой прямой и последовательного уточнения положения точки [math]\displaystyle{ \alpha }[/math].

На очередном шаге, имея отрезок [math]\displaystyle{ I_{n-1} }[/math], содержащий точку [math]\displaystyle{ \alpha }[/math], мы делим его на десять равных отрезков и выбираем из них тот отрезок [math]\displaystyle{ I_{n} }[/math], на котором лежит точка [math]\displaystyle{ \alpha }[/math]; в случае когда эта точка является концом двух соседних отрезков, из этих двух отрезков выбираем правый.

Продолжая этот процесс мы получим последовательность отрезков [math]\displaystyle{ I_0, I_1, \ldots }[/math] вида

[math]\displaystyle{ I_n = \left [ a_0 + \frac{a_1}{10^1} + \ldots + \frac{a_n}{10^n} \, ; \, a_0 + \frac{a_1}{10^1} + \ldots + \frac{a_n}{10^n} + \frac{1}{10^n} \right] }[/math]

где [math]\displaystyle{ a_0 }[/math] — целое неотрицательное, а [math]\displaystyle{ a_1, a_2, \ldots }[/math] — целые числа, удовлетворяющие неравенству [math]\displaystyle{ 0 \leqslant a_k \leqslant 9 }[/math].

Построенная последовательность отрезков [math]\displaystyle{ I_0, I_1, \ldots }[/math] обладает следующими свойствами:

• Отрезки последовательно вложены друг в друга: [math]\displaystyle{ I_0 \supset I_1 \supset I_2 \supset \ldots }[/math]
• Длина отрезков [math]\displaystyle{ |I_n| = 10^{-n}, \; n = 0, 1, 2, \ldots }[/math]
• Точка [math]\displaystyle{ \alpha }[/math] принадлежит всем отрезкам последовательности

Из этих условий следует, что [math]\displaystyle{ I_0, I_1, \ldots }[/math] есть система вложенных отрезков, длины которых стремятся к нулю при [math]\displaystyle{ n \to \infty }[/math], а точка [math]\displaystyle{ \alpha }[/math] есть общая точка всех отрезков системы. Отсюда вытекает, что последовательность левых концов отрезков сходится к точке [math]\displaystyle{ \alpha }[/math] (аналогичное утверждение справледливо и для последовательности правых концов), то есть

[math]\displaystyle{ a_0 + \frac{a_1}{10^1} + \ldots + \frac{a_n}{10^n} \to \alpha }[/math] при [math]\displaystyle{ n\to \infty }[/math]

Это значит, что ряд

[math]\displaystyle{ \sum_{k=0}^{\infty} a_k \cdot 10^{-k} }[/math]

сходится к числу [math]\displaystyle{ \alpha }[/math], и таким образом, десятичная дробь

[math]\displaystyle{ a_0{,}a_{1} a_{2} \ldots }[/math]

является представлением числа [math]\displaystyle{ \alpha }[/math]. Таким образом, найдено разложение неотрицательного числа [math]\displaystyle{ \alpha }[/math] в десятичную дробь.

Полученная десятичная дробь является бесконечной по построению. При этом может оказаться, что начиная с некоторого номера, все десятичные знаки после запятой суть нули, то есть дробь имеет вид

[math]\displaystyle{ a_0{,}a_1 \ldots a_n 000 \ldots }[/math]

Нетрудно видеть, что эта возможность имеет место в том случае, когда на некотором шаге точка [math]\displaystyle{ \alpha }[/math] совпадает с одной из точек деления числовой прямой. В этом случае отбрасывая в сумме

[math]\displaystyle{ \sum_{k=0}^{\infty} a_k \cdot 10^{-k} }[/math]

нулевые слагаемые, получим, что число [math]\displaystyle{ \alpha }[/math] также может быть представлено конечной десятичной дробью

[math]\displaystyle{ a_0{,} a_1 \ldots a_n }[/math]

Вообще, ясно, что приписывая в конец десятичной дроби после запятой любое количество нулей (в том числе бесконечное), мы не изменяем значение дроби. Таким образом, в данном случае число [math]\displaystyle{ \alpha }[/math] может быть представлено как конечной, так и бесконечной десятичной дробью (полученной из первой приписыванием бесконечного числа нулей).

Тем самым рассмотрен случай неотрицательного [math]\displaystyle{ \alpha }[/math]. В случае отрицательного [math]\displaystyle{ \alpha }[/math], в качестве десятичного представления этого числа можно взять представление противоположного ему положительного числа, взятое со знаком «минус».

Приведенный алгоритм дает способ разложения произвольного действительного числа в десятичную дробь. Тем самым доказана следующая

Теорема. Всякое действительное число может быть представлено в виде десятичной дроби.

О роли аксиомы Архимеда

Приведенный алгоритм разложения действительного числа в десятичную дробь существенно опирается на свойство системы действительных чисел, называемое аксиомой Архимеда.

Это свойство было использовано дважды в алгоритме. В самом начале построения выбиралось целое [math]\displaystyle{ a_0 }[/math], такое, что действительное число [math]\displaystyle{ \alpha }[/math] находится между [math]\displaystyle{ a_0 }[/math] и следующим целым [math]\displaystyle{ a_0 + 1 }[/math]:

[math]\displaystyle{ a_0 \leqslant \alpha \lt a_0 + 1, \; a_0 \in \mathbb{Z} }[/math]

Однако существование такого целого числа [math]\displaystyle{ a_0 }[/math] надо ещё доказать: нельзя исключать, например, возможность, когда, каково бы ни было целое [math]\displaystyle{ n }[/math], всегда имеет место неравенство [math]\displaystyle{ n \leqslant \alpha }[/math]. Если бы этот случай имел место, то, очевидно, нужного числа [math]\displaystyle{ a_0 }[/math] не нашлось бы.

Эта возможность как раз исключается аксиомой Архимеда, согласно которой каково бы ни было число [math]\displaystyle{ \alpha }[/math], всегда найдётся целое [math]\displaystyle{ n }[/math] такое, что [math]\displaystyle{ n \gt \alpha }[/math]. Теперь среди чисел [math]\displaystyle{ k= 1, \ldots, n }[/math] возьмём наименьшее, обладающее свойством [math]\displaystyle{ k \gt \alpha }[/math]. Тогда

[math]\displaystyle{ k - 1 \leqslant \alpha \lt k }[/math]

Искомое число найдено: [math]\displaystyle{ a_0 = k-1 }[/math].

Второй раз аксиома Архимеда неявно использовалась при доказательстве стремления к нулю длин отрезков последовательности [math]\displaystyle{ I_0, I_1, I_2, \ldots }[/math]:

[math]\displaystyle{ \lim_{n \to \infty} 10^{-n} = 0 }[/math]

Строгое доказательство данного предложения опирается на аксиому Архимеда. Докажем эквивалентное соотношение

[math]\displaystyle{ \lim_{n \to \infty} 10^{n} = \infty }[/math]

В соответствии с аксиомой Архимеда, каково бы ни было действительное число [math]\displaystyle{ E \gt 0 }[/math], последовательность натуральных чисел [math]\displaystyle{ 1, 2, \ldots }[/math] превзойдёт его, начиная с некоторого номера. А поскольку для всякого [math]\displaystyle{ n }[/math] имеет место неравенство

[math]\displaystyle{ 10^n \gt n }[/math]

то последовательность [math]\displaystyle{ 10^n }[/math] также превзойдёт [math]\displaystyle{ E }[/math], начиная с того же номера. В соответствии с определением предела числовой последовательности, это означает, что [math]\displaystyle{ \lim_{n \to \infty} 10^{n} = \infty }[/math].

Неоднозначность представления в виде десятичной дроби

См. также: 0,(9)

С помощью приведённого алгоритма мы можем для любого действительного числа [math]\displaystyle{ \alpha }[/math] построить десятичную дробь, представляющую данное число. Однако может случиться, что это же самое число [math]\displaystyle{ \alpha }[/math] может быть представлено в виде десятичной дроби и другим образом.

Неединственность представления чисел в виде десятичных дробей уже следует из того тривиального факта, что, приписывая конечной дроби справа после запятой нули, мы будем получать формально различные десятичные дроби, представляющие одно и то же число.

Однако, если даже считать дроби, полученные путём приписывания в конец друг другу конечного или бесконечного количества нулей, тождественными, представление некоторых действительных чисел всё же остаётся неединственным.

Рассмотрим например, десятичную дробь

[math]\displaystyle{ 0{,}99\ldots }[/math]

Согласно определению, эта дробь является представлением числа [math]\displaystyle{ 0 + 9/10 + 9/100 + \ldots = 1 }[/math]. Вместе с тем, это число может быть также представлено в виде десятичной дроби [math]\displaystyle{ 1{,}00\ldots }[/math]. В самом деле, вещественные числа [math]\displaystyle{ a,b }[/math] различны тогда и только тогда, когда между ними можно вставить ещё одно вещественное число, не совпадающее с самими [math]\displaystyle{ a,b. }[/math] Но между [math]\displaystyle{ 0{,}99\ldots }[/math] и [math]\displaystyle{ 1{,}00\ldots }[/math] никакого третьего числа вставить нельзя.

Этот пример можно обобщить. Можно показать, что дроби

[math]\displaystyle{ \pm a_0{,}a_1 \ldots a_{n-1} a_n 999 \ldots }[/math]

и

[math]\displaystyle{ \pm a_0{,}a_1 \ldots a_{n-1} (a_n+1) 000 }[/math]

где [math]\displaystyle{ a_n \neq 9 }[/math], представляют одно и то же действительное число.

Оказывается, этим общим примером исчерпываются все случаи неоднозначности представления действительных чисел в виде десятичных дробей. При этом мы, конечно, не рассматриваем тривиальные случаи дробей, полученные приписыванием нулей в конец друг другу, а также пару дробей [math]\displaystyle{ + 0{,}00 \ldots }[/math] и [math]\displaystyle{ - 0{,}00 \ldots }[/math].

Эти результаты можно суммировать в следующей теореме.

Теорема. Всякое действительное число [math]\displaystyle{ \alpha }[/math], не представимое в виде [math]\displaystyle{ p/10^s }[/math], где [math]\displaystyle{ p }[/math] — целое, [math]\displaystyle{ s }[/math] — целое неотрицательное, допускает единственное представление в виде десятичной дроби; при этом эта дробь является бесконечной.

Всякое действительное число вида [math]\displaystyle{ \alpha = p/10^s }[/math] может быть представлено в виде десятичной дроби более чем одним способом. Если [math]\displaystyle{ \alpha \neq 0 }[/math], то оно может быть представлено как в виде конечной десятичной дроби, а также бесконечной дроби, полученной приписыванием нулей в конец после запятой, так и в виде бесконечной дроби, оканчивающейся на [math]\displaystyle{ 999 \ldots }[/math]. Число [math]\displaystyle{ \alpha = 0 }[/math] может быть представлено дробями вида [math]\displaystyle{ +0{,}00 \ldots }[/math], а также дробями вида [math]\displaystyle{ -0{,}00 \ldots }[/math].

Замечание. Бесконечные дроби, оканчивающиеся на [math]\displaystyle{ 999\ldots }[/math], получаются, если в приведённом выше алгоритме всегда выбирать левый отрезок вместо правого.

Лишние нули и погрешность

Основная статья: Округление

Следует отметить, что, с точки зрения приближённых вычислений, запись десятичной дроби с нулями в конце не совсем тождественна записи без этих нулей.

Принято считать, что, если погрешность не указана, то абсолютная погрешность десятичной дроби равна половине единицы последнего выписанного разряда, т.е. число получено в соответствии с правилами округления. Например, запись «3,7» означает, что абсолютная погрешность равна 0,05. А в записи «3,700» абсолютная погрешность равна 0,0005. Другие примеры:

• «25» — абсолютная погрешность равна 0,5 (также такая запись может означать точное значение 25: например, 25 штук);
• «2,50∙10⁴» — абсолютная погрешность равна 50;
• «25,00» — абсолютная погрешность равна 0,005.

Периодические десятичные дроби

Определение и свойства

Бесконечная десятичная дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр. Другими словами, периодическая дробь — десятичная дробь, имеющая вид

[math]\displaystyle{ \pm a_0, a_1 \ldots a_m \underbrace{b_1 \ldots b_l} \underbrace{b_1 \ldots b_l} \ldots }[/math]

Такую дробь принято кратко записывать в виде

[math]\displaystyle{ \pm a_0, a_1 \ldots a_m ( b_1 \ldots b_l ) }[/math]

Повторяющаяся группа цифр [math]\displaystyle{ b_1 \ldots b_l }[/math] называется периодом дроби, количество цифр в этой группе — длиной периода.

Если в периодической дроби период следует сразу после запятой, то дробь называется чистой периодической. Если же между запятой и первым периодом имеются цифры, дробь называется смешанной периодической, а группа цифр после запятой до первого знака периода — предпериодом дроби. Например, дробь [math]\displaystyle{ 1{,}(23) = 1{,}2323 \ldots }[/math] является чистой периодической, а дробь [math]\displaystyle{ 0{,}1(23)=0{,}12323 \ldots }[/math] — смешанной периодической.

Основное свойство периодических дробей, благодаря которому их выделяют из всей совокупности десятичных дробей, заключается в том, что периодические дроби и только они представляют рациональные числа. Точнее, имеет место следующее предложение.

Теорема. Всякая бесконечная периодическая десятичная дробь представляет рациональное число. Обратно, если рациональное число раскладывается в бесконечную десятичную дробь, то эта дробь является периодической.

Можно показать, что чисто периодические дроби соответствуют рациональным числам, в записи которых в виде несократимой дроби [math]\displaystyle{ p/q }[/math] знаменатель [math]\displaystyle{ q }[/math] не имеет простых делителей [math]\displaystyle{ 2 }[/math] и [math]\displaystyle{ 5 }[/math], а также рациональным числам [math]\displaystyle{ p/q }[/math], у которых знаменатель [math]\displaystyle{ q }[/math] имеет только простые делители [math]\displaystyle{ 2 }[/math] и [math]\displaystyle{ 5 }[/math]. Соответственно, смешанные периодические дроби соответствуют несократимым дробям [math]\displaystyle{ p/q }[/math], знаменатель [math]\displaystyle{ q }[/math] которых имеет как простые делители [math]\displaystyle{ 2 }[/math] или [math]\displaystyle{ 5 }[/math], так и отличные от них.

Преобразование периодической десятичной дроби в обыкновенную

Предположим, что дана периодическая десятичная дробь [math]\displaystyle{ x=0{,}(1998) }[/math] с периодом 4. Заметим, что домножив её на [math]\displaystyle{ 10^4 = 10000 }[/math], получим большую дробь [math]\displaystyle{ 10000x=1998{,}(1998) }[/math] с теми же цифрами после запятой. Отняв целую часть ([math]\displaystyle{ 1998 }[/math]), на которую увеличилась дробь после её умножения, получаем исходную дробь ([math]\displaystyle{ x }[/math]):
[math]\displaystyle{ 10000x-1998=x }[/math]
[math]\displaystyle{ \Rightarrow }[/math]
[math]\displaystyle{ 10000x-x=1998 }[/math]
[math]\displaystyle{ \Rightarrow }[/math]
[math]\displaystyle{ x=\frac{1998}{9999}=\frac{222}{1111} }[/math]

Произношение десятичных дробей

В русском языке десятичные дроби читаются так: сначала произносится целая часть, потом слово «целых» (или «целая»), потом дробная часть так, как если бы всё число состояло только из этой части, то есть числитель дроби — количественное числительное женского рода (одна, две, восемь и т.д.), а знаменатель — порядковое числительное (десятая, сотая, тысячная, десятитысячная и т.д.).

Например: 5,45 — пять целых, сорок пять сотых.

Для более длинных чисел иногда десятичную часть разбивают по степеням тысячи. Например: 0,123 456 — ноль целых, сто двадцать три тысячных, четыреста пятьдесят шесть миллионных.

Однако на практике часто как более рациональное, превалирует такое произношение: целая часть, союз «и» (часто опускается), дробная часть.

Например: 5,45 — пять и сорок пять; (пять — сорок пять).

Для периодических десятичных дробей произносят часть числа до периода (выраженную целым числом в случае чистой периодической дроби или конечной десятичной дробью в случае смешанной периодической дроби), а затем добавляют число в периоде. Например: 0,1(23) — ноль целых, одна десятая и двадцать три в периоде; 2,(6) — две целых и шесть в периоде.

История

Десятичные дроби впервые встречаются в Китае примерно с III века н. э. при вычислениях на счётной доске (суаньпань). В письменных источниках десятичные дроби ещё некоторое время изображали в традиционном (не позиционном) формате, но постепенно позиционная система вытеснила традиционную.

Тимуридский математик и астроном Джамшид Гияс-ад-дин аль-Каши (1380—1429) в трактате «Ключ арифметики» объявил себя изобретателем десятичных дробей, хотя они встречались в трудах Ал-Уклидиси, жившего на 5 веков раньше.

В Европе первоначально десятичные дроби записывали как целые числа в некотором оговоренном масштабе; например, тригонометрические таблицы Региомонтана (1467) содержали значения, увеличенные в 100000 раз и затем округлённые до целого. Первые десятичные дроби в Европе ввёл Иммануил Бонфис около 1350 года, в 1579 году их употребление пытался пропагандировать Виет. Но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585).

См. также

• Десятичный разделитель
• Десятичная система счисления
• Обыкновенная дробь
• Непрерывная дробь

Ссылки

• ЕГЭ математика. Периодическая дробь
• Задачи по теме «обыкновенные и десятичные дроби»
• Семёнова Л. Периодические дроби.