Числа Бернулли

Числители и знаменатели дроби чисел Бернулли составляют последовательность A027641 в OEIS и последовательность A027642 в OEIS соответственно;
[math]\displaystyle{ B_0 = 1 }[/math]
[math]\displaystyle{ B_1 = -\frac12 }[/math]
[math]\displaystyle{ B_2 = \frac16 }[/math]
[math]\displaystyle{ B_3 = 0 }[/math]
[math]\displaystyle{ B_4 = -\frac1{30} }[/math]
[math]\displaystyle{ B_5 = 0 }[/math]
[math]\displaystyle{ B_6 = \frac1{42} }[/math]
[math]\displaystyle{ B_7 = 0 }[/math]
[math]\displaystyle{ B_8 = -\frac1{30} }[/math]
[math]\displaystyle{ B_9 = 0 }[/math]
[math]\displaystyle{ B_{10} = \frac5{66} }[/math]
[math]\displaystyle{ B_{11} = 0 }[/math]
[math]\displaystyle{ B_{12} = -\frac{691}{2730} }[/math]
[math]\displaystyle{ B_{13} = 0 }[/math]
[math]\displaystyle{ B_{14} = \frac76 }[/math]
[math]\displaystyle{ B_{15} = 0 }[/math]
[math]\displaystyle{ B_{16} = -\frac{3617}{510} }[/math]
[math]\displaystyle{ B_{17} = 0 }[/math]
[math]\displaystyle{ B_{18} = \frac{43867}{798} }[/math]
[math]\displaystyle{ B_{19} = 0 }[/math]
[math]\displaystyle{ B_{20} = -\frac{174611}{330} }[/math]
[math]\displaystyle{ B_{22}=\frac{854513}{138} }[/math]
[math]\displaystyle{ B_{24}=-\frac{236364091}{2730} }[/math]
[math]\displaystyle{ B_{26}=\frac{8553103}{6} }[/math]
[math]\displaystyle{ B_{28}=-\frac{23749461029}{870} }[/math]
[math]\displaystyle{ B_{30}=\frac{8615841276005}{14322} }[/math]
[math]\displaystyle{ B_{32}=-\frac{7709321041217}{510} }[/math]
[math]\displaystyle{ B_{34}=\frac{2577687858367}{6} }[/math]
[math]\displaystyle{ B_{36}=-\frac{26315271553053477373}{1919190} }[/math]
[math]\displaystyle{ B_{38}=\frac{2929993913841559}{6} }[/math]
[math]\displaystyle{ B_{40}=-\frac{261082718496449122051}{13530} }[/math]
[math]\displaystyle{ B_{42}=\frac{1520097643918070802691}{1806} }[/math]
[math]\displaystyle{ B_{44}=-\frac{27833269579301024235023}{690} }[/math]
[math]\displaystyle{ B_{46}=\frac{596451111593912163277961}{282} }[/math]
[math]\displaystyle{ B_{48}=-\frac{5609403368997817686249127547}{46410} }[/math]
[math]\displaystyle{ B_{50}=\frac{495057205241079648212477525}{66} }[/math]

Чи́сла Берну́лли — последовательность рациональных чисел [math]\displaystyle{ B_0, B_1, B_2, \dots }[/math], впервые рассмотренная Якобом Бернулли в связи с вычислением суммы последовательных натуральных чисел, возведённых в одну и ту же степень:

[math]\displaystyle{ \sum_{n=0}^{N-1} n^k = \frac1{k + 1} \sum_{s=0}^k \binom{k + 1}{s} B_s N^{k + 1 - s}, }[/math]

где [math]\displaystyle{ \tbinom{k + 1}{s} = \tfrac{(k + 1)!}{s! \cdot (k + 1 - s)!} }[/math] — биномиальный коэффициент.

Некоторые авторы указывают другие определения, однако в большинстве современных учебников даётся такое же определение, как и здесь. При этом [math]\displaystyle{ B_1 = -\tfrac 1 2 }[/math]. Часть авторов (например, трёхтомник Фихтенгольца) использует определение, которое отличается от этого только знаком [math]\displaystyle{ B_k }[/math]. Кроме того, так как за исключением [math]\displaystyle{ B_1 }[/math] все числа Бернулли с нечётным номером равны 0, некоторые авторы используют обозначение «[math]\displaystyle{ B_n }[/math]» для [math]\displaystyle{ B_{2n} }[/math] или [math]\displaystyle{ |B_{2n}| }[/math].

Рекуррентная формула

Для чисел Бернулли существует следующая рекуррентная формула:

[math]\displaystyle{ B_0 = 1, }[/math]

[math]\displaystyle{ B_n = \frac{-1}{n + 1} \sum_{k=1}^n \binom{n + 1}{k + 1} B_{n - k}, \quad n \in \mathbb{N}. }[/math]

Свойства

Все числа Бернулли с нечётными номерами, кроме [math]\displaystyle{ B_1 }[/math], равны нулю, а знаки чисел Бернулли с чётными номерами чередуются.
Числа Бернулли являются значениями многочленов Бернулли [math]\displaystyle{ B_n(x) }[/math] при [math]\displaystyle{ x = 0 }[/math]:

[math]\displaystyle{ B_n = B_n(0). }[/math]

Числа Бернулли часто входят в коэффициенты разложения элементарных функций в степенной ряд. Например:
- Экспоненциальная производящая функция для чисел Бернулли:
  [math]\displaystyle{ \frac x{e^x - 1} = \sum_{n=0}^\infty \frac{B_n}{n!} x^n, |x| \lt 2\pi, }[/math]
  
  [math]\displaystyle{ x \operatorname{ctg} x = \sum_{n=0}^\infty (-1)^n B_{2n} \frac{2^{2n}}{(2n)!} x^{2n}, |x| \lt \pi, }[/math]
  
  [math]\displaystyle{ \operatorname{tg} x = \sum_{n=1}^\infty |B_{2n}| \frac{2^{2n}(2^{2n} - 1)}{(2n)!} x^{2n-1}, |x| \lt \pi/2. }[/math]
Эйлер установил связь между числами Бернулли и значениями дзета-функции Римана ζ(s) при чётных s = 2k:
[math]\displaystyle{ B_{2k} = 2(-1)^{k+1} \frac{\zeta(2k)\,(2k)!}{(2\pi)^{2k}}. }[/math]

А также

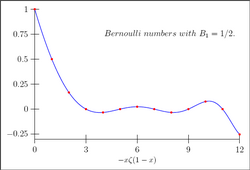
[math]\displaystyle{ B_n = -n\zeta(1 - n) }[/math] для всех натуральных n > 1.

[math]\displaystyle{ \int\limits_0^\infty \frac{x^{2n-1}\,dx}{e^{2\pi x} - 1} = \frac1{4n}|B_{2n}|, \quad n = 1, 2, \dots. }[/math]
Порядок роста чисел Бернулли даётся следующей асимптотической формулой:
[math]\displaystyle{ |B_n| \sim \frac {2\cdot n!}{(2\pi)^n} }[/math] при чётных [math]\displaystyle{ n \to \infty }[/math]. Из формулы, написанной выше, следует равносильность этой асимптотики и равенства: [math]\displaystyle{ \lim\limits_{k\to \infty} {\zeta(2k)} =1 \; \text{по} \; k\in\mathbb{Z} }[/math].

Получение чисел Бернулли из дзета-функции Римана

Литература

Бернуллиевы числа // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Абрамович В. Числа Бернулли // Квант. — 1974. — № 6. — С. 10—14.

Ссылки

Генератор Чисел Бернулли