Колоссально избыточное число

Колоссально избыточное число (CA от англ. colossally abundant number) — натуральное число [math]\displaystyle{ n }[/math], которое в определённом строгом смысле имеет много делителей: существует [math]\displaystyle{ \varepsilon \gt 0 }[/math] такое, что для всех [math]\displaystyle{ k \gt 1 }[/math]:
- [math]\displaystyle{ \frac{\sigma(n)}{n^{1+\varepsilon}}\geqslant\frac{\sigma(k)}{k^{1+\varepsilon}} }[/math],
где [math]\displaystyle{ \sigma }[/math] — функция суммы делителей[1]. Все колоссально избыточные числа также являются суперизбыточными числами, но обратное неверно.
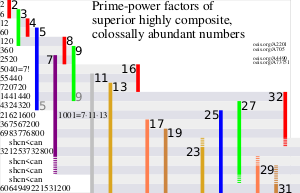
Первые 15 колоссально избыточных чисел[2] — 2, 6, 12, 60 , 120, 360, 2520, 5040, 55440, 720720, 1441440 , 4324320, 21621600, 367567200, 6983776800 — также являются первыми 15 весьма суперсоставными числами.
История

Впервые колоссально избыточные числа были изучены Рамануджаном, и его результаты должны были быть включены в его статью 1915 года о сверхсоставном числе[3]. К сожалению, издатель журнала, в который Рамануджан представил свою работу, Лондонское математическое общество, в то время испытывало финансовые затруднения, и Рамануджан согласился удалить некоторые аспекты работы, чтобы снизить стоимость печати[4]. Его выводы в основном были обусловлены гипотезой Римана, и с этим предположением он нашёл верхнюю и нижнюю границы размера колоссально избыточных чисел и доказал, что то, что впоследствии станет известным как неравенство Робина (см. ниже), выполняется для всех достаточно больших значений n[5].
Класс чисел был пересмотрен в несколько более сильной форме в статье Леонидаса Алаоглу и Пала Эрдёша 1944 года, в которой они пытались расширить результаты Рамануджана[6].
Свойства
Колоссально избыточные числа — это один из нескольких классов целых чисел, которые пытаются уловить понятие наличия множества делителей. Для положительного целого числа n функция суммы делителей σ (n) даёт сумму всех тех чисел, которые делят n, включая 1 и само n. Пауль Бахман показал, что в среднем σ(n) составляет около π2n / 6[7]. Теорема Грёнвалла, тем временем, говорит, что максимальный порядок σ(n) немного больше, в частности, существует возрастающая последовательность целых чисел n, такая, что для этих целых чисел σ(n) примерно того же размера, что и eγnlog(log(n)), где γ является постоянной Эйлера — Маскерони[7]. Следовательно, колоссально избыточные числа охватывают понятие наличия множества делителей, требуя от них максимизировать для некоторого [math]\displaystyle{ \varepsilon \gt 0 }[/math], значение функции
- [math]\displaystyle{ \frac{\sigma(n)}{n^{1+\varepsilon}} }[/math]
по всем значениям [math]\displaystyle{ n }[/math]. Результаты Бахмана и Грёнвалла гарантируют, что для любого [math]\displaystyle{ \varepsilon \gt 0 }[/math] эта функция имеет максимум и что по мере стремления ε к нулю эти максимумы будут увеличиваться. Таким образом, существует бесконечно много колоссально избыточных чисел, хотя они довольно редки, и только 22 из них меньше 1018[8].
Для каждого ε указанная выше функция имеет максимум, но не очевидно, и на самом деле неверно, что для каждого ε это максимальное значение единственно. Алаоглу и Эрдёш изучали, сколько различных значений n может дать одно и то же максимальное значение указанной выше функции для данного значения ε. Они показали, что для большинства значений ε будет единственное целое число n, максимизирующее функцию. Позже, однако, Эрдёш и Жан-Луи Николя показали, что для определённого набора дискретных значений ε может быть два или четыре различных значения n, дающих одно и то же максимальное значение[9].
В своей статье 1944 года Алаоглу и Эрдёш предположили, что соотношение двух последовательных колоссально избыточных чисел всегда было простым числом. Они показали, что это следует из частного случая гипотезы четырёх экспонент в теории трансцендентных чисел, в частности, что для любых двух различных простых чисел p и q только действительные числа t, для которых и pt и qt являются рациональными числами, являются положительными целыми числами. Используя соответствующий результат для трёх простых чисел — частный случай теоремы о шести экспонентах, который К. Л. Зигель доказал, — им удалось показать, что частное двух последовательных колоссально избыточных чисел всегда равно либо простому, либо полупростому числу, то есть числу, состоящему всего из двух простых множителей. Частное никогда не может быть квадратом простого числа.
Гипотеза Алаоглу и Эрдёша остаётся открытой, хотя она проверена как минимум вплоть до 107[10] Если это правда, это будет означать, что существует последовательность неотличимых простых чисел p1, p2, p3,... таких, что n-е колоссально избыточное число имело вид:
- [math]\displaystyle{ c_n = \prod_{i=1}^n p_{i}~. }[/math]
Предполагая, что гипотеза верна, эта последовательность простых чисел начинается с 2, 3, 2, 5, 2, 3, 7, 2 (последовательность A073751 в OEIS). Гипотеза Алаоглу и Эрдёша также означала бы, что никакое значение ε не даёт четырёх различных целых чисел n в качестве максимумов указанной выше функции.
Связь с гипотезой Римана
В 1980-х годах Гай Робин показал[11], что гипотеза Римана эквивалентна утверждению, что следующее неравенство верно для всех [math]\displaystyle{ n }[/math] > 5040: (где [math]\displaystyle{ \gamma }[/math] является постоянной Эйлера — Маскерони):
- [math]\displaystyle{ \sigma(n)\lt e^\gamma n \log\log n \approx 1.781072418 \cdot n \log\log n \,~. }[/math]
Известно, что это неравенство не выполняется для 27 чисел (последовательность A067698 в OEIS):
- 2, 3, 4, 5, 6, 8, 9, 10, 12, 16, 18, 20, 24, 30, 36, 48, 60, 72, 84, 120, 180, 240, 360, 720, 840, 2520, 5040
Робин показал, что если гипотеза Римана верна, то [math]\displaystyle{ n }[/math] = 5040 — это последнее целое число, для которого она не выполняется. Неравенство теперь известно как неравенство Робина после его работы. Известно, что неравенство Робина, если оно когда-либо не соблюдается, не сработает для колоссально избыточного числа «n»; таким образом, гипотеза Римана фактически эквивалентна неравенству Робина, справедливому для каждого колоссально избыточного числа n > 5040.
В 2001–2002 годах Лагариас[8] продемонстрировал альтернативную форму утверждения Робина, которая не требует исключений, используя гармоническое число вместо логарифма:
- [math]\displaystyle{ \sigma(n) \lt H_n + \exp(H_n)\log(H_n)~. }[/math]
Или, кроме 8 исключений из n = 1, 2, 3, 4, 6, 12, 24, 60:
- [math]\displaystyle{ \sigma(n) \lt \exp(H_n)\log(H_n)~. }[/math]
Ссылки
- ↑ К. Бриггс, Избыточные числа и гипотеза Римана, Экспериментальная математика 15:2 (2006), стр. 251–256, doi:10.1080/10586458.2006.10128957.
- ↑ последовательность A004490 в OEIS
- ↑ С. Рамануджан, "Сверхсоставные числа", Труды Лондонского математического общества 14 (1915), стр. 347–407, MR: 2280858.
- ↑ С. Рамануджан, Сборник статей, Челси, 1962.
- ↑ С. Рамануджан, "Сверхсоставные числа. Аннотировано с предисловием Ж.-Л. Николя и Г. Робина", Журнал Рамануджана 1 (1997), стр. 119–153.
- ↑ Алаоглу, Л. & Эрдёш, П. (1944), О сверхсоставных и похожих числах, Труды Американского математического общества Т. 56: 448–469, doi:10.2307/1990319, <http://www.renyi.hu/~p_erdos/1944-03.pdf> Архивная копия от 12 ноября 2017 на Wayback Machine.
- ↑ 7,0 7,1 Г. Харди, Э. М. Райт, Введение в теорию чисел. 5-е издание, Изд. Оксфордского университета, Оксфорд, 1979.
- ↑ 8,0 8,1 Дж. К. Лагариас, Элементарная задача, эквивалентная гипотезе Римана Архивная копия от 10 октября 2014 на Wayback Machine, Американский математический ежемесячник 109 (2002), стр. 534–543.
- ↑ П. Эрдёш, Ж.-Л. Николя, "Распределение сверхизбыточных чисел", Бюллетень Французского математического общества 103 (1975), стр. 65–90.
- ↑ Н. Дж. А. Слоун, Простые числа, которые при умножении по порядку дают последовательность колоссально избыточных чисел Архивная копия от 16 апреля 2021 на Wayback Machine, Он-лайн энциклопедия целочисленных последовательностей. Фонд OEIS.
- ↑ G. Robin, "Большие значения функции суммы делителей и гипотеза Римана", Журнал чистой и прикладной математики 63 (1984), стр. 187–213.
Внешние ссылки
- Кейт Бриггс о колоссально избыточных числах и гипотезе Римана
- Вступление в MathWorld
- Примечания к гипотезе Римана и избыточные числа
- Подробнее о формулировке Робина RH
Для улучшения этой статьи желательно: |