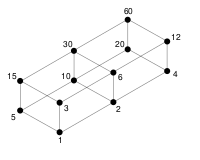
Сверхсоставное число

Первые четыре сверхсоставных числа: 1, 2, 4, 6 и их разложения на делители

Сверхсоставное число — натуральное число с бо́льшим числом делителей, чем любое меньшее натуральное число.

История

Термин был предложен Рамануджаном в 1915 году. Однако Жан-Пьер Кахане рассматривал их раньше, и, возможно, они были известны уже Платону, который описал число 5040 как идеальное количество граждан города, так как 5040 имеет больше делителей, чем любое меньшее число.

Примеры

В таблице представлены первые 38 сверхсоставных числа (последовательность A002182 в OEIS).

номер	Сверхсоставное	разложение на простые	число делителей	разложение на праймориалы
1	1		1
2	2	[math]\displaystyle{ 2 }[/math]	2	[math]\displaystyle{ 2 }[/math]
3	4	[math]\displaystyle{ 2^2 }[/math]	3	[math]\displaystyle{ 2^2 }[/math]
4	6	[math]\displaystyle{ 2\cdot 3 }[/math]	4	[math]\displaystyle{ 6 }[/math]
5	12	[math]\displaystyle{ 2^2\cdot 3 }[/math]	6	[math]\displaystyle{ 2\cdot 6 }[/math]
6	24	[math]\displaystyle{ 2^3\cdot 3 }[/math]	8	[math]\displaystyle{ 2^2\cdot 6 }[/math]
7	36	[math]\displaystyle{ 2^2\cdot 3^2 }[/math]	9	[math]\displaystyle{ 6^2 }[/math]
8	48	[math]\displaystyle{ 2^4\cdot 3 }[/math]	10	[math]\displaystyle{ 2^3\cdot 6 }[/math]
9	60	[math]\displaystyle{ 2^2\cdot 3\cdot 5 }[/math]	12	[math]\displaystyle{ 2\cdot 30 }[/math]
10	120	[math]\displaystyle{ 2^3\cdot 3\cdot 5 }[/math]	16	[math]\displaystyle{ 2^2\cdot 30 }[/math]
11	180	[math]\displaystyle{ 2^2\cdot 3^2\cdot 5 }[/math]	18	[math]\displaystyle{ 6\cdot 30 }[/math]
12	240	[math]\displaystyle{ 2^4\cdot 3\cdot 5 }[/math]	20	[math]\displaystyle{ 2^3\cdot 30 }[/math]
13	360	[math]\displaystyle{ 2^3\cdot 3^2\cdot 5 }[/math]	24	[math]\displaystyle{ 2\cdot 6\cdot 30 }[/math]
14	720	[math]\displaystyle{ 2^4\cdot 3^2\cdot 5 }[/math]	30	[math]\displaystyle{ 2^2\cdot 6\cdot 30 }[/math]
15	840	[math]\displaystyle{ 2^3\cdot 3\cdot 5\cdot 7 }[/math]	32	[math]\displaystyle{ 2^2\cdot 210 }[/math]
16	1260	[math]\displaystyle{ 2^2\cdot 3^2\cdot 5\cdot 7 }[/math]	36	[math]\displaystyle{ 6\cdot 210 }[/math]
17	1680	[math]\displaystyle{ 2^4\cdot 3\cdot 5\cdot 7 }[/math]	40	[math]\displaystyle{ 2^3\cdot 210 }[/math]
18	2520	[math]\displaystyle{ 2^3\cdot 3^2\cdot 5\cdot 7 }[/math]	48	[math]\displaystyle{ 2\cdot 6\cdot 210 }[/math]
19	5040	[math]\displaystyle{ 2^4\cdot 3^2\cdot 5\cdot 7 }[/math]	60	[math]\displaystyle{ 2^2\cdot 6\cdot 210 }[/math]
20	7560	[math]\displaystyle{ 2^3\cdot 3^3\cdot 5\cdot 7 }[/math]	64	[math]\displaystyle{ 6^2\cdot 210 }[/math]
21	10080	[math]\displaystyle{ 2^5\cdot 3^2\cdot 5\cdot 7 }[/math]	72	[math]\displaystyle{ 2^3\cdot 6\cdot 210 }[/math]
22	15120	[math]\displaystyle{ 2^4\cdot 3^3\cdot 5\cdot 7 }[/math]	80	[math]\displaystyle{ 2\cdot 6^2\cdot 210 }[/math]
23	20160	[math]\displaystyle{ 2^6\cdot 3^2\cdot 5\cdot 7 }[/math]	84	[math]\displaystyle{ 2^4\cdot 6\cdot 210 }[/math]
24	25200	[math]\displaystyle{ 2^4\cdot 3^2\cdot 5^2\cdot 7 }[/math]	90	[math]\displaystyle{ 2^2\cdot 30\cdot 210 }[/math]
25	27720	[math]\displaystyle{ 2^3\cdot 3^2\cdot 5\cdot 7\cdot 11 }[/math]	96	[math]\displaystyle{ 2\cdot 6\cdot 2310 }[/math]
26	45360	[math]\displaystyle{ 2^4\cdot 3^4\cdot 5\cdot 7 }[/math]	100	[math]\displaystyle{ 6^3\cdot 210 }[/math]
27	50400	[math]\displaystyle{ 2^5\cdot 3^2\cdot 5^2\cdot 7 }[/math]	108	[math]\displaystyle{ 2^3\cdot 30\cdot 210 }[/math]
28	55440	[math]\displaystyle{ 2^4\cdot 3^2\cdot 5\cdot 7\cdot 11 }[/math]	120	[math]\displaystyle{ 2^2\cdot 6\cdot 2310 }[/math]
29	83160	[math]\displaystyle{ 2^3\cdot 3^3\cdot 5\cdot 7\cdot 11 }[/math]	128	[math]\displaystyle{ 6^2\cdot 2310 }[/math]
30	110880	[math]\displaystyle{ 2^5\cdot 3^2\cdot 5\cdot 7\cdot 11 }[/math]	144	[math]\displaystyle{ 2^3\cdot 6\cdot 2310 }[/math]
31	166320	[math]\displaystyle{ 2^4\cdot 3^3\cdot 5\cdot 7\cdot 11 }[/math]	160	[math]\displaystyle{ 2\cdot 6^2\cdot 2310 }[/math]
32	221760	[math]\displaystyle{ 2^6\cdot 3^2\cdot 5\cdot 7\cdot 11 }[/math]	168	[math]\displaystyle{ 2^4\cdot 6\cdot 2310 }[/math]
33	277200	[math]\displaystyle{ 2^4\cdot 3^2\cdot 5^2\cdot 7\cdot 11 }[/math]	180	[math]\displaystyle{ 2^2\cdot 30\cdot 2310 }[/math]
34	332640	[math]\displaystyle{ 2^5\cdot 3^3\cdot 5\cdot 7\cdot 11 }[/math]	192	[math]\displaystyle{ 2^2\cdot 6^2\cdot 2310 }[/math]
35	498960	[math]\displaystyle{ 2^4\cdot 3^4\cdot 5\cdot 7\cdot 11 }[/math]	200	[math]\displaystyle{ 6^3\cdot 2310 }[/math]
36	554400	[math]\displaystyle{ 2^5\cdot 3^2\cdot 5^2\cdot 7\cdot 11 }[/math]	216	[math]\displaystyle{ 2^3\cdot 30\cdot 2310 }[/math]
37	665280	[math]\displaystyle{ 2^6\cdot 3^3\cdot 5\cdot 7\cdot 11 }[/math]	224	[math]\displaystyle{ 2^3\cdot 6^2\cdot 2310 }[/math]
38	720720	[math]\displaystyle{ 2^4\cdot 3^2\cdot 5\cdot 7\cdot 11\cdot 13 }[/math]	240	[math]\displaystyle{ 2^2\cdot 6\cdot 30030 }[/math]

Разложение на простые

В разложении сверхсоставных чисел участвуют самые маленькие простые множители, и при этом не слишком много одних и тех же.

По основной теореме арифметики каждое натуральное число [math]\displaystyle{ n }[/math] имеет единственное разложение на простые:

[math]\displaystyle{ n = p_1^{c_1} \times p_2^{c_2} \times \cdots \times p_k^{c_k}\qquad (1) }[/math]

где [math]\displaystyle{ p_1 \lt p_2 \lt \cdots \lt p_k }[/math] простые, и степени [math]\displaystyle{ c_i }[/math] положительные целые числа. Число делителей [math]\displaystyle{ d(n) }[/math] числа [math]\displaystyle{ n }[/math] можно выразить следующим образом:

[math]\displaystyle{ d(n) = (c_1 + 1) \times (c_2 + 1) \times \cdots \times (c_k + 1).\qquad (2) }[/math]

Таким образом, для сверхсоставного числа [math]\displaystyle{ n }[/math] выполняется следующее

• Числа [math]\displaystyle{ p_1, p_2, \dots, p_k }[/math] являются первыми [math]\displaystyle{ k }[/math] простыми числами.
• Последовательность степеней должна быть невозрастающей, то есть [math]\displaystyle{ c_1 \geq c_2 \geq \cdots \geq c_k }[/math].
  • Это свойство равносильно тому, что сверхсоставное число является произведением праймориалов.
• За исключением двух особых случаев n = 4 И N = 36, последняя степень [math]\displaystyle{ c_k }[/math] равна единице.

В частности 1, 4 и 36 являются единственными сверхсоставными квадратами.

Хотя описанные выше условия являются необходимыми, они не являются достаточными. Например, 96 = 2⁵ × 3 удовлетворяет всем вышеперечисленным условиям и имеет 12 делителей, но не является сверхсоставным, поскольку существует меньшее число 60, которое имеет то же число делителей.

Асимптотический рост и плотность

Существуют постоянные a и b, обе больше, чем 1, такие, что

[math]\displaystyle{ \ln(x)^a \le Q(x) \le \ln(x)^b, }[/math]

Где [math]\displaystyle{ Q(x) }[/math] обозначает число сверхсоставных чисел меньше либо равных [math]\displaystyle{ x }[/math].

Первая часть неравенства была доказана Палом Эрдешем в 1944 году; вторую доказал Жан-Луи Николас в 1988 году.

Известно также, что

[math]\displaystyle{ 1{,}13862 \lt \liminf \frac{\log Q(x)}{\log\log x} \le 1{,}44 }[/math]

и

[math]\displaystyle{ \limsup \frac{\log Q(x)}{\log\log x} \le 1{,}71. }[/math]

Свойства

• Все сверхсоставные числа, большие 6, являются избыточными.

• Не все сверхсоставные числа являются числами харшад по основанию 10;
  • первый контрпример это 245 044 800, это число имеет сумму цифр 27, но на 27 не делится.

См. также

• Высокототиентное число
• Таблица делителей
• Функция Эйлера

Ссылки

• Ramanujan, S. Highly composite numbers (неопр.) // Proc. London Math. Soc. (2). — 1915. — Т. 14. — С. 347—409. — doi:10.1112/plms/s2_14.1.347. (online Архивная копия от 3 сентября 2014 на Wayback Machine)
• Handbook of number theory I (неопр.). — Dordrecht: Springer-Verlag, 2006. — С. 45—46. — ISBN 1-4020-4215-9.
• Erdös, P. On highly composite numbers (неопр.) // Лондонское математическое общество. — 1944. — Т. 19. — С. 130—133. — doi:10.1112/jlms/19.75_part_3.130.
• Alaoglu, L. On highly composite and similar numbers (англ.) // Transactions of the American Mathematical Society. — 1944. — Vol. 56, no. 3. — P. 448—469. — doi:10.2307/1990319.
• Ramanujan, Srinivasa Highly composite numbers (англ.) // Ramanujan Journal : journal. — 1997. — Vol. 1, no. 2. — P. 119—153. — doi:10.1023/A:1009764017495. Annotated and with a foreword by Jean-Louis Nicolas and Guy Robin.

Ссылки

• Алгоритм вычисления высшей степени составных чисел
• Первые 10000 высшей степени составных чисел в качестве факторов
• Flammenkamp ахим, первый 779674 ГКН с Сигма,Тау, факторы
• Онлайн Сильно Составные Числа Калькулятор

Литература

• О. Оре. Приглашение в теорию чисел. — М.: Наука, 1980. — 128 с. — (выпуск 3 серии «Библиотечка квант»). — 150 000 экз.