Необычное число

Демонстрация палочками Кюизенера, что число 10 — необычное число, его наибольший простой делитель равен 5, что больше, чем √10 ≈ 3,16

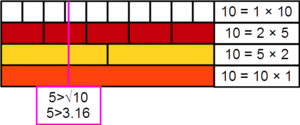
Необычное число — натуральное число [math]\displaystyle{ n }[/math], наибольший простой множитель которого строго больше [math]\displaystyle{ \sqrt{n} }[/math].

У [math]\displaystyle{ k }[/math]-гладкого числа все простые множители меньше или равны [math]\displaystyle{ k }[/math], поэтому необычное число не-[math]\displaystyle{ \sqrt{n} }[/math]-гладкое.

Все простые числа необычны. Для любого простого [math]\displaystyle{ p }[/math] его кратные, меньшие [math]\displaystyle{ p^2 }[/math], являются необычными, то есть [math]\displaystyle{ p, \dots, (p-1)p }[/math], у которых плотность [math]\displaystyle{ 1/p }[/math] в интервале [math]\displaystyle{ (p, p^2) }[/math].

Первые несколько необычных чисел:

2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 20, 21, 22, 23, 26, 28, 29, 31, 33, 34, 35, 37, 38, 39, 41, 42, 43, 44, 46, 47, 51, 52, 53, 55, 57, 58, 59, 61, 62, 65, 66, 67…

Первые несколько непростых необычных чисел:

6, 10, 14, 15, 20, 21, 22, 26, 28, 33, 34, 35, 38, 39, 42, 44, 46, 51, 52, 55, 57, 58, 62, 65, 66, 68, 69, 74, 76, 77, 78, 82, 85, 86, 87, 88, 91, 92, 93, 94, 95, 99, 102….

Если обозначить количество необычных чисел, меньших или равных [math]\displaystyle{ n }[/math], через [math]\displaystyle{ u(n) }[/math], то [math]\displaystyle{ u(n) }[/math] ведёт себя следующим образом:

[math]\displaystyle{ n }[/math]	[math]\displaystyle{ u(n) }[/math]	[math]\displaystyle{ u(n)/n }[/math]
10	6	0,6
100	67	0,67
1000	715	0,72
10000	7319	0,73
100000	73322	0,73
1000000	731660	0,73
10000000	7280266	0,73
100000000	72467077	0,72
1000000000	721578596	0,72

Рихард Шрёппель установил в 1972 году, что асимптотическая вероятность того, что случайно выбранное число является необычным, равна ln (2):

[math]\displaystyle{ \lim_{n \rightarrow \infty} \frac{u(n)}{n} = \ln(2) = 0{,}693147 \dots }[/math]

Ссылки

• Вайсстайн, Эрик. Грубое число (англ.) на сайте Wolfram MathWorld.