Числа Фибоначчи

Черепица с квадратами, длина сторон которых является последовательными числами Фибоначчи: 1, 1, 2, 3, 5, 8, 13 и 21

Спираль Фибоначчи: приближение золотой спирали, созданной путём рисования круговых дуг, соединяющих противоположные углы квадратов в мозаике Фибоначчи; (см. предыдущее изображение)

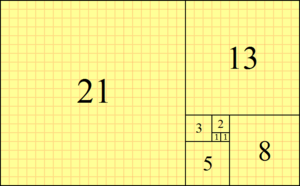
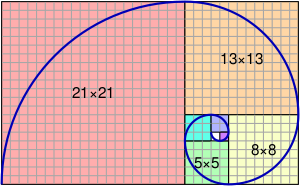
Чи́сла Фибона́ччи (вариант написания — Фибона́чи) — элементы числовой последовательности

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, … (последовательность A000045 в OEIS),

в которой первые два числа равны 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел. Названы в честь средневекового математика Леонардо Пизанского (известного как Фибоначчи).

Правда, в некоторых книгах, особенно в старых^{[каких?]}, член $F_0$, равный нулю, опускается — тогда последовательность Фибоначчи начинается с $F_1=F_2=1$.

Говоря более формально, последовательность чисел Фибоначчи $\{F_n\}$ задаётся линейным рекуррентным соотношением:

$F_0=0,F_1=1,F_n=F_{n-1}+F_{n-2}$,

где $n⩾2,n\in \mathbb{Z}$.

Иногда числа Фибоначчи рассматривают и для отрицательных значений $n$ как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. Соответственно, члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: $F_n=F_{n+2}-F_{n+1}$:

n	…	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10	…
$F_n$	…	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55	…

Легко заметить, что $F_{-n}=(-1{)}^{n+1}{F}_n$.

Происхождение

Количество пар кроликов образуют последовательность Фибоначчи

Страница Книги абака (лат. Liber abaci) Фибоначчи из Национальной центральной библиотеки Флоренции.
В правом блоке демонстрируется последовательность Фибоначчи. Позиции от 0 до 12 обозначены тёмным цветом римскими цифрами, а значения красным цветом индо-арабскими цифрами

Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении) намного раньше, чем стала известна в Европе.

Образец длиной n может быть построен путём добавления S к образцу длиной n − 1, либо L к образцу длиной n − 2 — и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».

На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Книга абака» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, где условия таковы: изначально дана новорождённая пара кроликов (самец и самка); со второго месяца после своего рождения кролики начинают спариваться и производить новую пару кроликов, причём уже каждый месяц; кролики никогда не умирают, — а в качестве искомого выдвигает количество пар кроликов через год.

• В начале первого месяца есть только одна новорождённая пара (1).
• В конце первого месяца по-прежнему только одна пара кроликов, но уже спарившаяся (1).
• В конце второго месяца первая пара рождает новую пару и опять спаривается (2).
• В конце третьего месяца первая пара рождает ещё одну новую пару и спаривается, вторая пара только спаривается (3).
• В конце четвёртого месяца первая пара рождает ещё одну новую пару и спаривается, вторая пара рождает новую пару и спаривается, третья пара только спаривается (5).

В конце $n$-го месяца количество пар кроликов будет равно количеству пар в предыдущем месяце плюс количеству новорождённых пар, которых будет столько же, сколько пар было два месяца назад, то есть $F_n=F_{n-2}+F_{n-1}$. Возможно, эта задача также оказалась первой, моделирующей экспоненциальный рост популяции.

Название «последовательность Фибоначчи» впервые было использовано теоретиком XIX века Эдуардом Люка.

Формула Бине

Формула Бине выражает в явном виде значение $F_n$ как функцию от n:

$F_n=\frac{{\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n}{\sqrt{5}}=\frac{{\phi }^n-(-\phi {)}^{-n}}{\phi -(-\phi {)}^{-1}}=\frac{{\phi }^n-(-\phi {)}^{-n}}{2\phi -1},$

где $\phi =\frac{1+\sqrt{5}}{2}$ — золотое сечение и $\phi$ и $(-\phi {)}^{-1}=1-\phi$ являются корнями характеристического уравнения $x^2-x-1=0.$ Вообще, аналогичная формула существует для любой линейной рекуррентной последовательности, какой служит и последовательность Фибоначчи.

Обоснование

Преобразуем характеристическое уравнение $x^2-x-1=0$ к виду $x^2=x+1,$ умножим обе части на $x$: $x^3=x^2+x$ — и заменим в этой сумме $x^2$ на $x+1$, что мы можем сделать в силу характеристического уравнения. Получим $x^3=x^2+x=(x+1)+x=2x+1.$ Затем продолжим так же умножать на $x$ и преобразовывать $x^2$, следуя первоначальному уравнению:

$\begin{array}{rl}{x}^4& =2x^2+x=2(x+1)+x=\\ & =3x+2,\\ x^5& =3x^2+2x=3(x+1)+2x=\\ & =5x+3,\\ x^6& =5x^2+3x=5(x+1)+3x=\\ & =8x+5,\\ x^7& =8x^2+5x=8(x+1)+5x=\\ & =13x+8,\\ & \cdots \end{array}$

Таким образом образуется общее уравнение: $x^n=F_{n}x+F_{n-1}.$ Чтобы это уравнение обратить в верное равенство и отсюда выразить сами числа Фибоначчи, нужно подставить корни $\phi$ и $-{\phi }^{-1}:$

$\{\begin{array}{l}{\phi }^n=F_n\phi +F_{n-1},\\ (-\phi {)}^{-n}=-F_n{\phi }^{-1}+F_{n-1},\end{array}$

${\phi }^n-(-\phi {)}^{-n}=F_n[\phi -(-\phi {)}^{-1}],{\phi }^n+(-\phi {)}^{-n}\cdot {\phi }^2=F_{n-1}(1+{\phi }^2),$

$\text{Missing argument for sqrt}$

Следствие и обобщение

Из формулы Бине следует, что для всех $n⩾0$ число $F_n$ есть округление $\frac{{\phi }^n}{\sqrt{5}},$ то есть $F_n=\lfloor \frac{{\phi }^n}{\sqrt{5}}\rceil .$ В частности, при $n\to \mathrm{\infty }$ справедлива асимптотика $F_n\sim \frac{{\phi }^n}{\sqrt{5}}.$

Формула Бине может быть аналитически продолжена следующим образом:

$F_z=\frac{1}{\sqrt{5}}({\phi }^z-\frac{\cos \pi z}{{\phi }^z}).$

При этом соотношение $F_{z+2}=F_{z+1}+F_z$ выполняется для любого комплексного числа z.

Тождества

Иллюстрация формулы для суммы квадратов первых n чисел Фибоначчи

• $F_1+F_2+F_3+\cdots +F_n=F_{n+2}-1.$

Доказательстворазвернуть

Докажем формулу индукцией по n:

База индукции: $n=0:$

$F_0=F_2-1=0.$

Шаг индукции: пусть утверждение для $n$ верно:

$F_1+F_2+F_3+...+F_n=F_{n+2}-1.$

Тогда надо доказать утверждение для $n+1:$

$F_1+F_2+F_3+...+F_n+F_{n+1}=F_{n+3}-1.$

Раскладываем $F_{n+3}$ на $F_{n+2}$ и $F_{n+1}:$

$F_1+F_2+F_3+...+F_n+F_{n+1}=F_{n+2}+F_{n+1}-1$

Сокращаем обе части на $F_{n+1}:$

$F_1+F_2+F_3+...+F_n=F_{n+2}-1,$

что и требовалось доказать. ∎

• $F_1+F_3+F_5+\cdots +F_{2n-1}=F_{2n}.$

Доказательстворазвернуть

Докажем формулу индукцией по n:

База индукции: $n=1:$

$F_1=F_2=1.$

Шаг индукции: Пусть утверждение для $n$ верно:

$F_1+F_3+F_5+\cdots +F_{2n-1}=F_{2n}.$

Тогда надо доказать утверждение для $n+1:$

$F_1+F_3+F_5+\cdots +F_{2n-1}+F_{2n+1}=F_{2n+2}.$

Раскладываем $F_{2n+2}$ на $F_{2n+1}$ и $F_{2n}:$

$F_1+F_3+F_5+\cdots +F_{2n-1}+F_{2n+1}=F_{2n+1}+F_{2n}.$

Сокращаем обе части на $F_{2n+1}:$

$F_1+F_3+F_5+\cdots +F_{2n-1}=F_{2n}.$

что и требовалось доказать. ∎

• $F_2+F_4+F_6+\cdots +F_{2n}=F_{2n+1}-1.$

Это тождество можно доказать вычитанием первого из второго: $\begin{array}{rl}(F_1+F_2+\cdots +F_{2n})-(F_1+F_3+\cdots +F_{2n-1})& =F_{2n+2}-1-F_{2n},\\ F_2+F_4+\cdots +F_{2n}& =F_{2n+1}-1.\end{array}$

• $F_{n+1}{F}_{n+2}-F_n{F}_{n+3}=(-1{)}^n.$
• $F_1^2+F_2^2+F_3^2+\cdots +F_n^2=F_n{F}_{n+1}$ (см. рис.).
• $F_n^2+F_{n+1}^2=F_{2n+1}.$
• $F_{2n}=F_{n+1}^2-F_{n-1}^2.$
• $F_{3n}=F_{n+1}^3+F_n^3-F_{n-1}^3.$
• $F_{5n}=25F_n^5+25(-1{)}^n{F}_n^3+5F_n.$
• $F_{n+1}=C_n^0+C_{n-1}^1+C_{n-2}^2+\dots$, где $C_n^k$ — биномиальные коэффициенты.

И более общие формулы:

• $F_{n+m}=F_{n-1}{F}_m+F_n{F}_{m+1}=F_{n+1}{F}_{m+1}-F_{n-1}{F}_{m-1}.$
• $F_{(k+1)n}=F_{n-1}{F}_{kn}+F_n{F}_{kn+1}.$
• $F_n=F_l{F}_{n-l+1}+F_{l-1}{F}_{n-l}.$
• Числа Фибоначчи представляются значениями континуант на наборе единиц: $F_{n+1}=K_n(1,\dots ,1),$ то есть

  $F_{n+1}=det\left(\begin{array}{ccccc}1& 1& 0& \cdots & 0\\ -1& 1& 1& \ddots & ⋮\\ 0& -1& \ddots & \ddots & 0\\ ⋮& \ddots & \ddots & \ddots & 1\\ 0& \cdots & 0& -1& 1\end{array}\right)$, а также $F_{n+1}=det\left(\begin{array}{ccccc}1& i& 0& \cdots & 0\\ i& 1& i& \ddots & ⋮\\ 0& i& \ddots & \ddots & 0\\ ⋮& \ddots & \ddots & \ddots & i\\ 0& \cdots & 0& i& 1\end{array}\right),$

где матрицы имеют размер $n\times n$ и где i — мнимая единица.

• Числа Фибоначчи можно выразить через многочлены Чебышёва:

  $F_{n+1}=(-i{)}^n{U}_n\left(\frac{-i}{2}\right),$

  $F_{2n+2}=U_n\left(\frac{3}{2}\right).$

• Для любого n справедливо

  ${\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)}^n=\left(\begin{array}{cc}{F}_{n+1}& F_n\\ F_n& F_{n-1}\end{array}\right).$

• Как следствие, подсчёт определителей даёт тождество Кассини:

$(-1{)}^n=F_{n+1}{F}_{n-1}-F_n^2.$

• С равенством Кассини сопряжено более общее утверждение, названное в честь Эжена Каталана:$F_n^2-F_{n-r}{F}_{n+r}=(-1{)}^{n-r}{F}_r^2.$

• $F_{n+1}=\frac{F_n+\sqrt{5F_n^2+4(-1{)}^n}}{2}.$
  Это утверждение выводится из тождества Кассини при помощи основного соотношения чисел Фибоначчи: $(-1{)}^n=F_{n+1}(F_{n+1}-F_n)-F_n^2$ $⟺$ $0={F_{n+1}}^2-F_{n+1}{F}_n-(F_n^2+(-1{)}^n).$

Свойства

Тринадцать ($F_7$) способов расположения длинных (красные) и коротких слогов (серые) в каденции длины шесть: пять ($F_5$) заканчивается длинным слогом и восемь ($F_6$) — коротким

Числа Фибоначчи — это суммы «мелких» диагоналей (показаны красным) треугольника Паскаля

Последовательные наклоны плоскости и график приближений к золотому сечению, рассчитанному путём деления каждого числа Фибоначчи на предыдущее

• Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, то есть $(F_m,F_n)=F_{(m,n)}.$ Следствия:
  • $F_m$ делится на $F_n$ тогда и только тогда, когда $m$ делится на $n$ (за исключением $n=2$). В частности, $F_m$ делится на $F_3=2$ (то есть является чётным) только для $m=3k;$ $F_m$ делится на $F_4=3$ только для $m=4k;$ $F_m$ делится на $F_5=5$ только для $m=5k$ и т. д.
  • $F_m$ может быть простым только для простых $m$ (с единственным исключением $m=4$). Например, число $F_{13}=233$ простое, и его индекс 13 также прост. Но, даже если число $m$ простое, число $F_m$ не всегда оказывается простым, и наименьший контрпример — $F_{19}=4181=37\cdot 113.$ Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
• Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен $x^2-x-1$ имеет корни $\phi$ и $-\frac{1}{\phi }.$
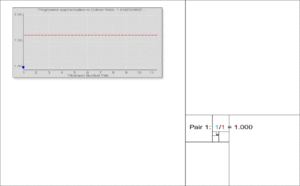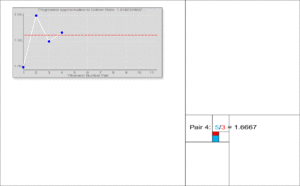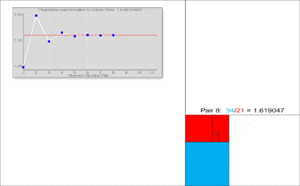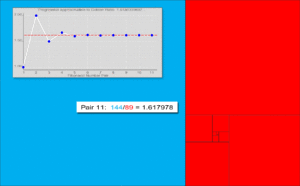
• Отношения $\frac{F_{n+1}}{F_n}$ являются подходящими дробями золотого сечения $\varphi :$ в частности, $\underset{n\to \mathrm{\infty }}{lim}\frac{F_{n+1}}{F_n}=\phi .$
• Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы

  $F_{n+1}=\sum _{k=0}^{\lfloor n/2\rfloor }(\genfrac{}{}{0ex}{}{n-k}{k}).$

• В 1964 году Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12:

  $F_0=0^2=0,$ $F_1=1^2=1,$ $F_2=1^2=1,$ $F_{12}={12}^2=144.$

• Производящей функцией последовательности чисел Фибоначчи является:

  $x+x^2+2x^3+3x^4+5x^5+\cdots =\sum _{n=0}^{\mathrm{\infty }}{F}_n{x}^n=\frac{x}{1-x-x^2}$

  • В частности, 1/998,999 = 0.001001002003005008013021…
• Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена

  $z(x,y)=2x{y}^4+x^2{y}^3-2x^3{y}^2-y^5-x^{4}y+2y$

на множестве неотрицательных целых чисел x и y.

• Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
• Период чисел Фибоначчи по модулю натурального числа $n$ называется периодом Пизано и обозначается $\pi (n)$. Периоды Пизано $\pi (n)$ образуют последовательность:

  1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS).

  • В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом $\pi (10)=60$, последняя пара цифр чисел Фибоначчи образует последовательность с периодом $\pi (100)=300$, последние три цифры — с периодом $\pi (1000)=1500,$ последние четыре — с периодом $\pi (10000)=15000,$ последние пять — с периодом $\pi (100000)=150000$ и т. д.
• Натуральное число $N$ является числом Фибоначчи тогда и только тогда, когда $5N^2+4$ или $5N^2-4$ является квадратом.
• Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.
• Число Фибоначчи $F_{n+2}=F_{n+1}+F_n$ равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних единиц. При этом $F_{n+1}$ равно количеству таких кортежей, начинающихся с нуля, а $F_n$ — начинающихся с единицы.
• Произведение любых $n$ подряд идущих чисел Фибоначчи делится на произведение первых $n$ чисел Фибоначчи.
• Бесконечная сумма чисел, обратных числам Фибоначчи, сходится, его сумма («обратная постоянная Фибоначчи») равна 3,359884...

Вариации и обобщения

Основная статья: Обобщение чисел Фибоначчи

• Числа трибоначчи
• Числа Фибоначчи являются частным случаем последовательностей Люка $F_n=U_n(1,-1)$.
  • При этом их дополнением являются числа Люка $L_n=V_n(1,-1)$.

В других областях

Жёлтая ромашковая головка, показывающая расположение в 21 (синяя) и 13 (аква) спиралей. Такие схемы, включающие последовательные числа Фибоначчи, встречаются у самых разных растений

Числа Фибоначчи в интерьере станции метро Ломоносовский проспект

Число возможных предков на линии наследования Х-хромосомы в данном поколении предков следует последовательности Фибоначчи (Хатчисон Л. Растущее семейное древо: сила ДНК в восстановлении семейных отношений)

Иллюстрация модели Фогеля для n = 1 ... 500

Существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространённый миф, который часто оказывается неточной подгонкой под желаемый результат.

В природе

• Филлотаксис (листорасположение) у растений описывается последовательностью Фибоначчи, если листья (почки) на однолетнем приросте (побеге, стебле) имеют так называемое спиральное листорасположение. При этом число последовательно расположенных листьев (почек) по спирали плюс один, а также число совершенных при этом полных оборотов спирали вокруг оси однолетнего прироста (побега, стебля) выражаются обычно первыми числами Фибоначчи.
• Семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи.

В искусстве

В поэзии чаще находят отношение «золотого сечения» (золотую пропорцию), связанное через формулу Бине с числами Фибоначчи. Например, в поэме Ш. Руставели «Витязь в тигровой шкуре» и на картинах художников.

Однако числа Фибоначчи встречаются и непосредственно в поэзии и в музыке

В кодировании

В теории кодирования предложены устойчивые так называемые «коды Фибоначчи», причём основание этих кодов — иррациональное число.

См. также

• Дерево Фибоначчи
• Метод Фибоначчи с запаздываниями
• Метод Фибоначчи поиска экстремума
• Фибоначчи
• Фибоначчиева система счисления
• Числа Бине
• Числа Леонардо
• Таблица Витхоффа
• Последовательность коров Нараяны
• Золотое сечение
• Пропорционирование

Примечания

↑ Показывать компактно

Литература

• Н. Н. Воробьёв. Числа Фибоначчи. — Наука, 1978. — Т. 39. — (Популярные лекции по математике).
• А. И. Маркушевич. Возвратные последовательности. — Гос. Издательство Технико-Теоретической Литературы, 1950. — Т. 1. — (Популярные лекции по математике).
• А. Н. Рудаков. Числа Фибоначчи и простота числа 2¹²⁷ − 1 // Математическое Просвещение, третья серия. — 2000. — Т. 4.
• Дональд Кнут. Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4.
• Дональд Кнут, Роналд Грэхем, Орен Паташник. Конкретная математика. Основание информатики = Concrete Mathematics. A Foundation for Computer Science. — М.: Мир; Бином. Лаборатория знаний, 2006. — С. 703. — ISBN 5-94774-560-7.
• Грант Аракелян. Математика и история золотого сечения. — М.: Логос, 2014. — С. 404. — ISBN 978-5-98704-663-0.
• Ball, Keith M (2003), 8: Fibonacci's Rabbits Revisited, Strange Curves, Counting Rabbits, and Other Mathematical Explorations, Princeton, NJ: Princeton University Press, ISBN 978-0-691-11321-0 .
• Beck, Matthias & Geoghegan, Ross (2010), The Art of Proof: Basic Training for Deeper Mathematics, New York: Springer, ISBN 978-1-4419-7022-0 .
• Bóna, Miklós (2011), A Walk Through Combinatorics (3rd ed.), New Jersey: World Scientific, ISBN 978-981-4335-23-2 .
  • Bóna, Miklós (2016), A Walk Through Combinatorics (4th Revised ed.), New Jersey: World Scientific, ISBN 978-981-3148-84-0 .
• Lemmermeyer, Franz (2000), Reciprocity Laws: From Euler to Eisenstein, Springer Monographs in Mathematics, New York: Springer, ISBN 978-3-540-66957-9 .
• Livio, Mario. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (англ.). — First trade paperback. — New York City: Broadway Books, 2003. — ISBN 0-7679-0816-3.
• Lucas, Édouard (1891), Théorie des nombres, vol. 1, Paris: Gauthier-Villars, Théorie des nombres в «Книгах Google», <https://archive.org/details/thoriedesnombr01lucauoft> .
• Pisano, Leonardo (2002), Fibonacci's Liber Abaci: A Translation into Modern English of the Book of Calculation, Sources and Studies in the History of Mathematics and Physical Sciences, Springer, ISBN 978-0-387-95419-6 

Ссылки

• Первые 300 чисел Фибоначчи (англ.).
• Числа Фибоначчи в природе (англ.).