Центрированное треугольное число

Центрированное треугольное число — это центрированное полигональное число, которое представляет треугольник с точкой в центре и все остальные окружающие точки находятся на треугольных слоях. Центрированное треугольное число для n задается формулой

[math]\displaystyle{ {{3n^2 + 3n + 2} \over 2}. }[/math]

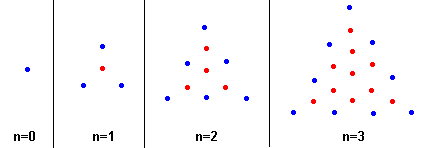
Следующая диаграмма показывает построение центрированных треугольных чисел: каждый предыдущий слой, показанный красным, окружается слоем новых точек, показанных синим.

Первые несколько центрированных треугольных чисел:

1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, 235, 274, 316, 361, 409, 460, 514, 571, 631, 694, 760, 829, 901, 976, 1054, 1135, 1219, 1306, 1396, 1489, 1585, 1684, 1786, 1891, 1999, 2110, 2224, 2341, 2461, 2584, 2710, 2839, 2971, …

Каждое центрированное треугольное число, начиная с 10, является суммой трех последовательных треугольных чисел. Также, каждое центрированное треугольное число при делении на 3 дает остаток 1 и частное (если оно положительно), есть предыдущее треугольное число.

Сумма первых n центрированных треугольных чисел есть магическая константа для магического квадрата n × n (n > 2).

Центрированное треугольное простое

Центрированное треугольное простое — это центрированное треугольное число, являющееся простым. Несколько первых центрированных треугольных простых:

19, 31, 109, 199, 409, 571, 631, 829, 1489, 1999, 2341, 2971, 3529, 4621, 4789, 7039, 7669, 8779, 9721, 10 459, …

(соответствующих n = 3, 4, 8, 11, 16, …)

Ссылки

• Lancelot Hogben: Mathematics for the Million (1936), republished by W. W. Norton & Company (September 1993), ISBN 978-0-393-31071-9
• Weisstein, Eric W. Centered Triangular Number (англ.) на сайте Wolfram MathWorld.