Дедекиндово число

Эта статья написана в рамках энциклопедии Руниверсалис и находится на начальном уровне проработки
Материал из энциклопедии Руниверсалис
Не следует путать с дедекиндовыми сечениями — способом построения действительных чисел.
contradictionA and B and CA and BA and CB and C(A and B) or (A and C)(A and B) or (B and C)(A and C) or (B and C)ABC(A or B) and (A or C) and (B or C) <====> (A and B) or (A and C) or (B and C)(A or B) and (A or C)(A or B) and (B or C)(A or C) and (B or C)A or BA or CB or CA or B or Ctautology
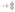link=http://upload.wikimedia.org/wikipedia/commons/thumb/5/57/Monotone_Boolean_functions_0%2C1%2C2%2C3.svg/1500px-Monotone_Boolean_functions_0%2C1%2C2%2C3.svg.png Архивная копия от 22 сентября 2017 на Wayback Machine Свободные дистрибутивные решётки монотонных булевых функций от 0, 1, 2 и 3 аргументов с 2, 3, 6 и 20 элементами соответственно (наведите мышь на правую диаграмму, чтобы видеть описание)

Дедекиндово число — число [math]\displaystyle{ M(n) }[/math], равное количеству монотонных булевых функций от [math]\displaystyle{ n }[/math] переменных. Эквивалентные определения: число антицепей подмножеств [math]\displaystyle{ n }[/math]-элементного множества; число элементов в свободной дистрибутивной решётке[англ.] с [math]\displaystyle{ n }[/math] производящими; число абстрактных симплициальных комплексов[англ.] с [math]\displaystyle{ n }[/math] элементами.

Последовательность [math]\displaystyle{ (M(n)) }[/math] — быстрорастущая, и хотя известны асимптотические оценки [math]\displaystyle{ M(n) }[/math][1][2][3] и точное выражение в виде суммы[4], но явной вычислительной формулы нет, в связи с чем точное нахождение дедекиндовых чисел остаётся крайне сложной вычислительной задачей; по состоянию на 2023 год точные значения известны для [math]\displaystyle{ n \leqslant 9 }[/math][5]:

2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788, 286386577668298411128469151667598498812366.

Числа от [math]\displaystyle{ M(0) }[/math] до [math]\displaystyle{ M(4) }[/math] вычислил Дедекинд в 1897 году и сформулировал задачу Дедекинда — найти способ вычисления последующих чисел. Число [math]\displaystyle{ M(5) }[/math] вычислил Чёрч в 1940 году[6], результат опроверг гипотезу Биркгофа, что [math]\displaystyle{ M(n) }[/math] всегда делится на [math]\displaystyle{ (2n-1)(2n-2) }[/math][6]. Числа [math]\displaystyle{ M(6) }[/math], [math]\displaystyle{ M(7) }[/math], [math]\displaystyle{ M(8) }[/math], [math]\displaystyle{ M(9) }[/math] были вычислены соответственно в 1946[7], 1965[8][9], 1991[10] и 2023[11] годах.

Для нахождения [math]\displaystyle{ M(8) }[/math] использовался суперкомпьютер Cray 2[англ.]. Число [math]\displaystyle{ M(9) }[/math] было получено двумя независимыми группами математиков: Кристиан Якель из Германии применил техники анализа формальных понятий и для вычислительной процедуры использовал графический ускоритель (5311 машиночаса на Nvidia A100[англ.]); второй группе математиков из Бельгии потребовалось 47 тыс. машиночасов вычислений на ПЛИС Stratix[англ.] 10 GX под управлением суперкомпьютера Noctua 2[12], занявших около трёх месяцев[13][14]. Обе группы получили одинаковый результат вычислений числа [math]\displaystyle{ M(9) }[/math], Якель опубликовал препринт на три дня раньше бельгийских коллег.

Если [math]\displaystyle{ n }[/math] чётно, то [math]\displaystyle{ M(n) }[/math] также должно быть чётным[15].

Точная формула для вычисления дедекиндовых чисел на основе логического определения антицепей была выведена в 1988 году[4]:

[math]\displaystyle{ M(n)=\sum_{k=1}^{2^{2^n}} \prod_{j=1}^{2^n-1} \prod_{i=0}^{j-1} \left(1-b_i^k b_j^k\prod_{m=0}^{\log_2 i} (1-b_m^i+b_m^i b_m^j)\right) }[/math],

где [math]\displaystyle{ b_i^k }[/math] является [math]\displaystyle{ i }[/math]-м битом числа [math]\displaystyle{ k }[/math], который может быть записан с помощью округления вниз:

[math]\displaystyle{ b_i^k=\left\lfloor\frac{k}{2^i}\right\rfloor - 2\left\lfloor\frac{k}{2^{i+1}}\right\rfloor }[/math],

однако она бесполезна для практического вычисления значений [math]\displaystyle{ M(n) }[/math] для больших [math]\displaystyle{ n }[/math] ввиду большого числа членов суммирования.

В 2014 году был найден ещё один вариант формулы, с помощью которой суммированием можно найти дедекиндовы числа:

[math]\displaystyle{ M(n+2)=\sum_{\alpha,\beta\in M_n} \left(|[\bot,\alpha]|2^{C_\alpha,\beta}|[\beta,\top]|\right) }[/math]

Эта формула позволяет разложить решетку антицепей на подрешетки в пространствах меньшей размерности.

Логарифм дедекиндова числа можно оценить с помощью границ:

[math]\displaystyle{ {n\choose \lfloor n/2\rfloor}\leqslant \log_2 M(n)\leqslant {n\choose \lfloor n/2\rfloor}\left(1+O\left(\frac{\log n}{n}\right)\right) }[/math],

где неравенство слева подсчитывает число антицепей, в которых каждое множество имеет в точности [math]\displaystyle{ \lfloor n/2\rfloor }[/math] элементов; правая часть неравенства установлена в 1975 году[1].

В 1981 году[2] были даны более точные оценки[16]:

[math]\displaystyle{ M(n)=(1+o(1)) 2^{n\choose \lfloor n/2\rfloor}\exp a(n) }[/math]

для чётных [math]\displaystyle{ n }[/math] и:

[math]\displaystyle{ M(n)=(1+o(1)) 2^{n\choose \lfloor n/2\rfloor + 1}\exp (b(n)+c(n)) }[/math]

для нечётных [math]\displaystyle{ n }[/math], где

[math]\displaystyle{ a(n)={n\choose n/2-1}(2^{-n/2} + n^2 2^{-n-5} - n2^{-n-4}) }[/math],
[math]\displaystyle{ b(n)={n\choose (n-3)/2}(2^{-(n+3)/2} + n^2 2^{-n-6} - n2^{-n-3}) }[/math],
[math]\displaystyle{ c(n)={n\choose (n-1)/2}(2^{-(n+1)/2} + n^2 2^{-n-4}) }[/math].

Основная идея этих оценок заключается в том, что в большинстве антицепей все множества имеют размеры, очень близкие к [math]\displaystyle{ n/2 }[/math][16]. Для [math]\displaystyle{ n=2, 4, 6, 8 }[/math] формула даёт оценку, которая имеет ошибку в 9,8 %, 10,2 %, 4,1 % и −3,3 % соответственно[17].

Пример

Для [math]\displaystyle{ n=2 }[/math] существует шесть монотонных булевых функций и шесть антицепей подмножеств двухэлементного множества [math]\displaystyle{ \{x,y\} }[/math]:

  • функция [math]\displaystyle{ f(x,y) = \bot }[/math], игнорирующая входные значения и всегда возвращающая [math]\displaystyle{ \bot }[/math], соответствует пустой антицепи [math]\displaystyle{ \varnothing }[/math];
  • логическая конъюнкция [math]\displaystyle{ f(x,y)=x\wedge y }[/math] соответствует антицепи [math]\displaystyle{ \{\{x,y\}\} }[/math], содержащей единственное множество [math]\displaystyle{ \{x,y\} }[/math];
  • функция [math]\displaystyle{ f(x,y)=x }[/math], игнорирующая второй аргумент и возвращающая первый аргумент, соответствует антицепи [math]\displaystyle{ \{\{x\}\} }[/math], содержащей единственное множество [math]\displaystyle{ \{x\} }[/math];
  • функция [math]\displaystyle{ f(x,y)=y }[/math], игнорирующая первый аргумент и возвращающая второй аргумент, соответствует антицепи [math]\displaystyle{ \{\{y\}\} }[/math], содержащей единственное множество [math]\displaystyle{ \{y\} }[/math];
  • логическая дизъюнкция [math]\displaystyle{ f(x,y)=x \vee y }[/math] соответствует антицепи [math]\displaystyle{ \{\{x\},\{y\}\} }[/math], содержащей два множества [math]\displaystyle{ \{x\} }[/math] и [math]\displaystyle{ \{y\} }[/math];
  • функция [math]\displaystyle{ f(x,y)=\top }[/math], игнорирующая входные значения и всегда возвращающая истинное значение, соответствует антицепи [math]\displaystyle{ \{\varnothing\} }[/math], содержащей только пустое множество.

Примечания

  1. ↑ 1,0 1,1 Kleitman, Markowsky, 1975.
  2. ↑ 2,0 2,1 Коршунов, 1981.
  3. ↑ Kahn, 2002.
  4. ↑ 4,0 4,1 Kisielewicz, 1988.
  5. ↑ последовательность A000372 в OEIS
  6. ↑ 6,0 6,1 Church, 1940.
  7. ↑ Ward, 1946.
  8. ↑ Church, 1965.
  9. ↑ Berman, Köhler, 1976.
  10. ↑ Wiedemann, 1991.
  11. ↑ Christian Jäkel. A computation of the ninth Dedekind Number // Arxiv.org. — 2023. — arXiv:2304.00895.
  12. ↑ Noctua 2 - BullSequana XH2000, AMD EPYC 7763 64C 2.45GHz, InfiniBand HDR100 | TOP500
  13. ↑ Александр Дубов. Математики нашли девятое дедекиндово число. В нем оказалось 42 знака. Это 286386577668298411128469151667598498812366. N + 1 (27 июня 2023).
  14. ↑ Lennart Van Hirtum, Patrick De Causmaecker, Jens Goemaere, Tobias Kenter, Heinrich Riebler, Michael Lass, Christian Plessl. A computation of D(9) using FPGA Supercomputing. — arXiv:2304.03039.
  15. ↑ Yamamoto, 1953.
  16. ↑ 16,0 16,1 Zaguia, 1993.
  17. ↑ Brown, K. S., <https://www.mathpages.com/home/kmath094/kmath094.htm> 

Литература

  • Joel Berman, Peter Köhler. Cardinalities of finite distributive lattices // Mitt. Math. Sem. Giessen. — 1976. — Т. 121. — С. 103–124.
  • Randolph Church. Numerical analysis of certain free distributive structures // Duke Mathematical Journal. — 1940. — Т. 6. — С. 732–734. — doi:10.1215/s0012-7094-40-00655-x..
  • Randolph Church. Enumeration by rank of the free distributive lattice with 7 generators // Notices of the American Mathematical Society. — 1965. — Т. 11. — С. 724.. Как процитировано Видерманом (Wiedemann (1991)).
  • Richard Dedekind. Über Zerlegungen von Zahlen durch ihre größten gemeinsamen Teiler // Gesammelte Werke. — 1897. — Т. 2. — С. 103–148.
  • Jeff Kahn. Entropy, independent sets and antichains: a new approach to Dedekind's problem // Proceedings of the American Mathematical Society. — 2002. — Т. 130, вып. 2. — С. 371–378. — doi:10.1090/S0002-9939-01-06058-0.
  • Andrzej Kisielewicz. A solution of Dedekind's problem on the number of isotone Boolean functions // Journal für die Reine und Angewandte Mathematik. — 1988. — Т. 386. — С. 139–144. — doi:10.1515/crll.1988.386.139.
  • Kleitman D., Markowsky G. On Dedekind's problem: the number of isotone Boolean functions. II // Transactions of the American Mathematical Society. — 1975. — Т. 213. — С. 373–390. — doi:10.2307/1998052..
  • Коршунов А. Д. О числе монотонных булевых функций // Проблемы кибернетики. — 1981. — Т. 38. — С. 5–108.
  • Morgan Ward. Note on the order of free distributive lattices // Bulletin of the American Mathematical Society. — 1946. — Т. 52. — С. 423. — doi:10.1090/S0002-9904-1946-08568-7.
  • Doug Wiedemann. A computation of the eighth Dedekind number // Order[англ.]. — 1991. — Т. 8, вып. 1. — С. 5–6. — doi:10.1007/BF00385808..
  • Koichi Yamamoto. Note on the order of free distributive lattices // Science Reports of the Kanazawa University. — 1953. — Т. 2, вып. 1. — С. 5–6.
  • Nejib Zaguia. Isotone maps: enumeration and structure // Finite and Infinite Combinatorics in Sets and Logic (Proc. NATO Advanced Study Inst., Banff, Alberta, Canada, May 4, 1991) / Sauer N. W., Woodrow R. E., Sands B.. — Kluwer Academic Publishers, 1993. — С. 421–430.
Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Дедекиндово_число&oldid=15970507