Дедекиндово сечение

Дедеки́ндово сече́ние — один из способов построения вещественных чисел из рациональных.

Множество вещественных чисел определяется как множество дедекиндовых сечений. На них возможно продолжить операции сложения и умножения.

История

Метод был введён в 1872 году Рихардом Дедекиндом.

Аналогичное построение для геометрических величин неявно присутствует в «Началах» Евклида, а именно, в книге V определение 5 звучит следующим образом:

Говорят, что величины находятся в том же отношении первая ко второй и третья к четвёртой, если равнократные первой и третьей одновременно больше, одновременно равны или одновременно меньше равнократных второй и четвёртой каждая каждой при какой бы то ни было кратности, если взять их в соответствующем порядке (9, 10, 11, 12)..

Близкие идеи опубликовал в 1849 году французский математик Жозеф Бертран.

Определение

Дедекиндово сечение — это разбиение множества рациональных чисел [math]\displaystyle{ \mathbb{Q} }[/math] на два подмножества [math]\displaystyle{ A }[/math] (нижнее, или левое) и [math]\displaystyle{ B }[/math] (верхнее, или правое) такие, что:

1. [math]\displaystyle{ a\lt b }[/math] для любых [math]\displaystyle{ a\in A }[/math] и [math]\displaystyle{ b\in B }[/math],
2. [math]\displaystyle{ B }[/math] не имеет наименьшего элемента.

Далее дедекиндово сечение обозначается [math]\displaystyle{ (A, B) }[/math] (хотя было бы достаточно указать одно из этих множеств, второе дополняет его до [math]\displaystyle{ \mathbb Q }[/math]).

Если множество [math]\displaystyle{ A }[/math] имеет наибольший элемент, то дедекиндово сечение можно отождествить с этим рациональным числом. В противном случае сечение определяет иррациональное число, которое больше всех чисел множества [math]\displaystyle{ A }[/math] и меньше всех чисел множества [math]\displaystyle{ B }[/math]. Определив на полученном множестве сечений арифметические операции и порядок, мы получаем поле вещественных чисел, причём каждое сечение определяет одно и только одно вещественное число.

Пример

Дедекиндово сечение √2

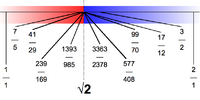
Вещественному числу [math]\displaystyle{ \sqrt 2 }[/math] соответствует дедекиндово сечение, для которого:

множество [math]\displaystyle{ A=\{x \in\mathbb Q\mid x\lt 0 \lor x^2\lt 2\}. }[/math]

множество [math]\displaystyle{ B=\{x \in\mathbb Q\mid x\gt 0 \land x^2\gt 2\}; }[/math]

Интуитивно можно представить себе, что для того, чтобы определить [math]\displaystyle{ \sqrt 2 }[/math], мы рассекли множество на две части: все числа, что левее [math]\displaystyle{ \sqrt 2 }[/math], и все числа, что правее [math]\displaystyle{ \sqrt 2 }[/math]; соответственно, [math]\displaystyle{ \sqrt 2 }[/math] равен точной нижней грани множества [math]\displaystyle{ B }[/math].

Упорядоченность дедекиндовых сечений

Введём во множестве сечений порядок. Сначала определим, что два сечения [math]\displaystyle{ (A, B) }[/math] и [math]\displaystyle{ (C, D) }[/math] равны, если [math]\displaystyle{ A=C }[/math] (тогда и [math]\displaystyle{ B=D }[/math]). Далее определим:

[math]\displaystyle{ (A, B) \lt (C, D) }[/math], если [math]\displaystyle{ A \subset C }[/math] и при этом [math]\displaystyle{ A \ne C. }[/math]

Нетрудно проверить, что все требования линейного порядка выполнены. Кроме того, для рациональных чисел новый порядок совпадает со старым.

Из данного определения порядка следует:

Теорема о приближении. Любое вещественное число может быть с любой точностью приближено рациональными числами, то есть может быть заключено в интервал с рациональными границами произвольно малой длины.

Арифметика дедекиндовых сечений

Для определения арифметических действий с сечениями можно воспользоваться сформулированной в предыдущем разделе теоремой о приближении.

Пусть [math]\displaystyle{ \alpha, \beta }[/math] — вещественные числа. Согласно теореме о приближении, для них можно указать интервалы-приближения с рациональными границами:

[math]\displaystyle{ a_1\lt \alpha\lt a_2\quad b_1\lt \beta\lt b_2. }[/math]

Тогда суммой [math]\displaystyle{ \alpha + \beta }[/math] называется вещественное число, содержащееся во всех интервалах вида [math]\displaystyle{ (a_1+b_1, a_2+b_2). }[/math] Сумма вещественных чисел всегда существует, однозначно определена и для рациональных чисел совпадает с прежним определением суммы. Вычитание всегда возможно, поэтому относительно так определённой операции сложения вещественные числа образуют аддитивную группу.

Аналогично определяется умножение вещественных чисел, которое вместе со сложением превращает множество вещественных чисел в упорядоченное поле.

Вариации и обобщения

См. также: Пополнение Дедекинда — Макнейла

Дедекиндовы сечения можно аналогично определить не только для рациональных чисел, но и в любом другом линейно упорядоченном множестве. См. Полнота (теория порядка). Можно показать, что применение этой процедуры к множеству вещественных чисел [math]\displaystyle{ \mathbb R }[/math] даёт снова [math]\displaystyle{ \mathbb R. }[/math]

Аналог дедекиндовых сечений используется для построения сюрреальных чисел.

См. также

• Конструктивные способы определения вещественного числа

Литература

• Кудрявцев Л. Д. Дедекиндово сечение // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1979. — Т. 2: Д — Коо. — С. 65. — 1104 стб. : ил. — 150 000 экз.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 6-е. — М.: Наука, 1966. — Т. I. — 680 с.