Коллинеарность

Два коллинеарных противоположно направленных вектора

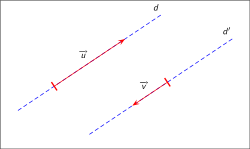
Коллинеа́рность (от лат. col — совместность и лат. linearis — линейный) — отношение параллельности векторов: два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой. Допусти́м синоним — «параллельные» векторы.

Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

Основное обозначение — [math]\displaystyle{ \vec{a}\parallel\vec{b} }[/math]; сонаправленные коллинеарные векторы обозначаются как [math]\displaystyle{ \vec{a}\upuparrows\vec{b} }[/math], противоположно направленные — [math]\displaystyle{ \vec{a}\uparrow\downarrow\vec{b} }[/math]. Если они не равны

Свойства

• Отношение коллинеарности рефлексивно ([math]\displaystyle{ \vec{a}||\vec{a} }[/math]).
• Отношение коллинеарности симметрично ([math]\displaystyle{ \vec{a}||\vec{b}\Leftrightarrow\vec{b}||\vec{a} }[/math]).
• Отношение коллинеарности ненулевых векторов транзитивно: если [math]\displaystyle{ \vec{a}||\vec{b},\ \vec{b}||\vec{c} }[/math] и [math]\displaystyle{ \vec{b}\ne\vec{0} }[/math], то [math]\displaystyle{ \vec{a}||\vec{c} }[/math].
• Нулевой вектор коллинеарен любому вектору.
• Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
• Если [math]\displaystyle{ \vec{a}||\vec{b} }[/math] и [math]\displaystyle{ \vec{b} \neq \vec{0} }[/math], то существует действительное число [math]\displaystyle{ \lambda }[/math] такое, что [math]\displaystyle{ \vec{a} = \lambda\vec{b}\; }[/math] (причём [math]\displaystyle{ \lambda \gt 0 }[/math], если векторы сонаправлены, и [math]\displaystyle{ \lambda \lt 0 }[/math], если они противонаправлены). Это соотношение также может служить критерием коллинеарности.
• Тройка векторов, содержащая пару коллинеарных векторов, компланарна.
• Векторы на плоскости коллинеарны тогда и только тогда, когда их псевдоскалярное произведение равно 0. На плоскости два неколлинеарных вектора [math]\displaystyle{ \vec{a} }[/math] и [math]\displaystyle{ \vec{b} }[/math] образуют базис. Это значит, что любой вектор [math]\displaystyle{ \vec{c} }[/math] можно представить в виде: [math]\displaystyle{ \vec{c}=x_1\vec{a}+x_2\vec{b} }[/math]. Тогда [math]\displaystyle{ \;\{x_1, x_2\} }[/math] будут координатами [math]\displaystyle{ \vec{c} }[/math] в данном базисе.
• Скалярное произведение коллинеарных векторов равно произведению их длин (взятых со знаком «минус», если векторы противоположно направлены).
• Векторное произведение коллинеарных векторов равно 0 — необходимое и достаточное условие коллинеарности.

Обобщения

Критерии коллинеарности позволяют определить это понятие для векторов, понимаемых не в геометрическом смысле, а как элементы произвольного линейного пространства.

Иногда коллинеарными называют точки, которые лежат на одной прямой.