Корень (математика)
- Это статья об извлечении корней. См. также Корень уравнения и Корень многочлена.
 |
Корень [math]\displaystyle{ n }[/math]-й степени из числа [math]\displaystyle{ a }[/math] определяется[1] как такое число [math]\displaystyle{ b }[/math], что [math]\displaystyle{ b^n=a. }[/math] Здесь [math]\displaystyle{ n }[/math] — натуральное число, называемое показателем корня (или степенью корня); как правило, оно больше или равно 2, потому что случай [math]\displaystyle{ n=1 }[/math] не представляет интереса.
Обозначение: [math]\displaystyle{ b=\sqrt[n]{a}, }[/math] символ (знак корня) в правой части называется радикалом. Число [math]\displaystyle{ a }[/math] (подкоренное выражение) чаще всего вещественное или комплексное, но существуют и обобщения для других математических объектов, например, вычетов, матриц и операторов, см. ниже #Вариации и обобщения.
Примеры для вещественных чисел:
- Корнями 2-й степени из числа 9 являются [math]\displaystyle{ +3 }[/math] и [math]\displaystyle{ -3, }[/math] у обоих этих чисел квадраты совпадают и равны 9
- [math]\displaystyle{ \sqrt[3]{\ 64}=4, }[/math] потому что [math]\displaystyle{ 4^3=64. }[/math]
- [math]\displaystyle{ \sqrt[3]{\frac{8}{27}}=\frac{2}{3}, }[/math] потому что [math]\displaystyle{ \left(\frac{2}{3}\right)^3=\frac{8}{27}. }[/math]
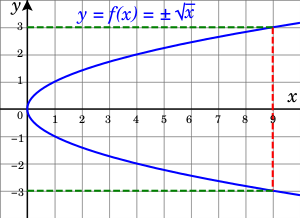
Как видно из первого примера, у вещественного корня чётной степени могут быть два значения (положительное и отрицательное), и это затрудняет работу с такими корнями, не позволяя использовать их в арифметических вычислениях. Чтобы обеспечить однозначность, вводится понятие арифметического корня (из неотрицательного вещественного числа), значение которого всегда неотрицательно, в первом примере это число [math]\displaystyle{ 3. }[/math] Кроме того, принято соглашение, по которому знак корня чётной степени из вещественного числа всегда обозначает арифметический корень[2][3]: [math]\displaystyle{ \sqrt[2]{9}=3. }[/math] Если требуется учесть двузначность корня, перед радикалом ставится знак плюс-минус[2]; например, так делается в формуле решения квадратного уравнения [math]\displaystyle{ ax^2+bx+c=0 }[/math]:
- [math]\displaystyle{ x_{1,2} = \frac{-b \pm \sqrt{b^2-4ac}}{2a} }[/math]
Вещественные корни чётной степени из отрицательных чисел не существуют. Из комплексного числа всегда можно извлечь корень любой степени, но результат определён неоднозначно — комплексный корень [math]\displaystyle{ n }[/math]-й степени из ненулевого числа имеет [math]\displaystyle{ n }[/math] различных значений (см. #Корни из комплексных чисел).
Операция извлечения корня и алгоритмы её реализации появились в глубокой древности в связи с практическими потребностями геометрии и астрономии, см. #История.
Определение и связанные понятия
Кроме приведенного выше, можно дать два равносильных определения корня[4]:
- Корень [math]\displaystyle{ n }[/math]-й степени из числа [math]\displaystyle{ a }[/math] есть решение [math]\displaystyle{ x }[/math] уравнения [math]\displaystyle{ x^n=a }[/math] (отметим, что решений может быть несколько или ни одного).
- Корень [math]\displaystyle{ n }[/math]-й степени из числа [math]\displaystyle{ a }[/math] есть корень многочлена [math]\displaystyle{ x^n-a, }[/math] то есть значение [math]\displaystyle{ x }[/math], при котором указанный многочлен равен нулю.
Операция вычисления [math]\displaystyle{ \sqrt[n]{a} }[/math] называется «извлечением корня [math]\displaystyle{ n }[/math]-й степени» из числа [math]\displaystyle{ a }[/math]. Это одна из двух операций, обратных по отношению к возведению в степень[5], а именно — нахождение основания степени [math]\displaystyle{ b }[/math] по известному показателю [math]\displaystyle{ n }[/math] и результату возведения в степень [math]\displaystyle{ a=b^n }[/math]. Вторая обратная операция, логарифмирование, находит показатель степени по известным основанию и результату.
Корни второй и третьей степени употребляются особенно часто и поэтому имеют специальные названия[5].
- Квадратный корень: [math]\displaystyle{ \sqrt{a}. }[/math] В этом случае показатель степени 2 обычно опускается, а термин «корень» без указания степени чаще всего подразумевает квадратный корень. Геометрически [math]\displaystyle{ \sqrt{a} }[/math] можно истолковать как длину стороны квадрата, площадь которого равна [math]\displaystyle{ a }[/math].
- Кубический корень: [math]\displaystyle{ \sqrt[3]{a}. }[/math] Геометрически [math]\displaystyle{ \sqrt[3]{a} }[/math] — это длина ребра куба, объём которого равен [math]\displaystyle{ a }[/math].
Корни из вещественных чисел
В данном разделе всюду [math]\displaystyle{ n }[/math] — натуральное число, [math]\displaystyle{ a,b }[/math] — вещественные числа. Корень [math]\displaystyle{ n }[/math]-й степени из вещественного числа [math]\displaystyle{ a }[/math], в зависимости от чётности [math]\displaystyle{ n }[/math] и знака [math]\displaystyle{ a }[/math], может иметь от 0 до 2 вещественных значений.
Общие свойства
- Корень нечётной степени из положительного числа — положительное число, однозначно определенное.
| [math]\displaystyle{ \sqrt[n]{a} = b }[/math], где [math]\displaystyle{ a, b \gt 0, }[/math] [math]\displaystyle{ n }[/math] — нечётное |
- Например, [math]\displaystyle{ \sqrt[3]{125} = 5, \ \sqrt[5]{32} = 2, \ \sqrt[15]{1} = 1 }[/math]
- Корень нечётной степени из отрицательного числа — отрицательное число, однозначно определенное.
| [math]\displaystyle{ \sqrt[n]{a} = b }[/math], где [math]\displaystyle{ a, b \lt 0, }[/math] [math]\displaystyle{ n }[/math] — нечётное |
- Например, [math]\displaystyle{ \sqrt[3]{-8} = -2, \ \sqrt[5]{-243} = -3, \ \sqrt[7]{-1} = -1 }[/math]
- Корень чётной степени из положительного числа имеет два значения с противоположными знаками, но равными по модулю.
| [math]\displaystyle{ \pm \sqrt[n]{a} = \pm b }[/math], где [math]\displaystyle{ a, b \gt 0, }[/math] [math]\displaystyle{ n }[/math] — чётное |
- Например, [math]\displaystyle{ \pm\sqrt{4} = \pm 2, \ \ \pm\sqrt[4]{81} = \pm 3, \ \ \pm\sqrt[10]{1024} = \pm 2 }[/math]
- Корень чётной степени из отрицательного числа не существует в области вещественных чисел, поскольку при возведении любого вещественного числа в степень с чётным показателем результатом будет неотрицательное число. Ниже будет показано, как извлекать такие корни в более широкой системе — множестве комплексных чисел (тогда значениями корня будут [math]\displaystyle{ n }[/math] комплексных чисел).
| [math]\displaystyle{ \sqrt[n]{a} }[/math] не существует в области вещественных чисел, если [math]\displaystyle{ a \lt 0, }[/math] [math]\displaystyle{ n }[/math] — чётное |
- Корень любой натуральной степени из нуля — ноль.
| [math]\displaystyle{ \sqrt[n]{0} = 0 }[/math] |
Предостережение
Как сказано выше: «Корень чётной степени из отрицательного числа не существует в области вещественных чисел». При этом в области комплексных чисел такой корень существует. Поэтому следует всегда учитывать, в какой числовой системе (вещественных или комплексных чисел) мы извлекаем корень.
- Пример. В области вещественных чисел, квадратный корень из [math]\displaystyle{ -9 }[/math] не существует.
- Пример. В области комплексных чисел, квадратный корень из [math]\displaystyle{ -9 }[/math] равен [math]\displaystyle{ \pm 3i. }[/math]
Арифметический корень

Выше уже говорилось, что корни чётной степени определены, вообще говоря, неоднозначно, и этот факт создаёт неудобства при их использовании. Поэтому было введено практически важное ограничение этого понятия[6].
Арифметический корень [math]\displaystyle{ n }[/math]-й степени из неотрицательного вещественного числа [math]\displaystyle{ a }[/math] — это неотрицательное число [math]\displaystyle{ b }[/math], для которого [math]\displaystyle{ b^n=a. }[/math] Обозначается арифметический корень знаком радикала.
Таким образом, арифметический корень, в отличие от корня общего вида (алгебраического), определяется только для неотрицательных вещественных чисел, а его значение всегда существует, однозначно[7] и неотрицательно. Например, квадратный корень из числа [math]\displaystyle{ 4 }[/math] имеет два значения: [math]\displaystyle{ 2 }[/math] и [math]\displaystyle{ -2 }[/math], из них арифметическим является первое.
Алгебраические свойства
Приведённые ниже формулы верны, прежде всего, для арифметических корней любой степени (кроме особо оговоренных случаев). Они справедливы также для корней нечётной степени, у которых допускаются и отрицательные подкоренные выражения[8].
- Взаимопогашение корня и степени:[9]
- для нечётного [math]\displaystyle{ n }[/math]: [math]\displaystyle{ \sqrt[n]{a^n} = a }[/math],
- для чётного [math]\displaystyle{ n }[/math]: [math]\displaystyle{ {\color{blue}\sqrt[{\color{black}n}] {\color{black}{a^n}}} = |a| }[/math]
- Если [math]\displaystyle{ a\lt b }[/math], то и [math]\displaystyle{ {\color{blue}\sqrt[{\color{black}n}] {\color{black}{a}}} \lt {\color{blue}\sqrt[{\color{black}n}] {\color{black}{b}}} }[/math]
Корень из произведения равен произведению корней из сомножителей:
- [math]\displaystyle{ {\color{blue}\sqrt[{\color{black}n}] {\color{black}{ab}}} = {\color{blue}\sqrt[{\color{black}n}] {\color{black}{a}}} {\color{blue}\sqrt[{\color{black}n}] {\color{black}{b}}} }[/math]
Аналогично для деления:
- [math]\displaystyle{ {\color{blue}\sqrt[{\color{black}n}] {\color{black}{\frac {a} {b}}}} = \frac{{\color{blue}\sqrt[{\color{black}n}] {\color{black} {a}}}} {{\color{blue}\sqrt[{\color{black}n}] {\color{black}{b}}}},\; b\ne 0 }[/math]
Следующее равенство есть определение возведения в дробную степень[10]:
- [math]\displaystyle{ a^{m/n} = {\color{blue}\sqrt[{\color{black}n}] {\color{black}{a^m}}} = \left({\color{blue}\sqrt[{\color{black}n}] {\color{black}{a}}}\right)^m = \left(a^{1/n}\right)^m }[/math]
Величина корня не изменится, если его показатель и степень подкоренного выражения разделить на одно и то же число (множитель показателя степени и показатель степени подкоренного выражения):
- [math]\displaystyle{ {\color{blue}\sqrt[{\color{black}nk}] {\color{black}{a^{mk}}}} = {\color{blue}\sqrt[{\color{black}n}] {\color{black}{a^m}}}, \; n,k \in \mathbb N. }[/math] Пример: [math]\displaystyle{ {\color{blue}\sqrt[{\color{black}6}] {\color{black}{64}}}={\color{blue}\sqrt[{\color{black}{2\cdot 3}}] {\color{black}{4^3}}} = {\color{blue}\sqrt {\color{black}{4}}} = 2 }[/math]
- [math]\displaystyle{ {\color{blue}\sqrt[{\color{black}n}] {\color{blue}\sqrt[{\color{black}k}] {\color{black} {a}}}} = {\color{blue}\sqrt[{\color{black}nk}] {\color{black}{a}}}, \; n,k \in \mathbb N }[/math]
Для корней нечётной степени укажем дополнительное свойство:
- [math]\displaystyle{ \sqrt[n]{-a} = - \sqrt[n]{a} }[/math]
Извлечение корня и возведение в дробную степень
Операция возведения в степень первоначально была введена как сокращённая запись операции умножения натуральных чисел: [math]\displaystyle{ m^n={\color{Gray}\underbrace{\color{Black}m\cdot m\cdot\dots\cdot m}_{\color{Black}n}} }[/math]. Следующим шагом было определение возведения в произвольную целую, в том числе отрицательную, степень: [math]\displaystyle{ m^{-n}=\frac{1}{m^n}. }[/math]
Операция извлечения арифметического корня позволяет определить возведение положительного числа в любую рациональную (дробную) степень[10]:
- [math]\displaystyle{ a^{\frac{m}{n}} = {\color{blue}\sqrt[{\color{black}n}] {\color{black}{a^m}}}, }[/math] [math]\displaystyle{ a\gt 0 }[/math]
При этом числитель [math]\displaystyle{ m }[/math] дроби [math]\displaystyle{ \frac{m}{n} }[/math] может иметь знак. Свойства расширенной операции в основном аналогичны возведению в целую степень.
Это определение означает, что извлечение корня и обратное к нему возведение в степень фактически объединяются в одну алгебраическую операцию. В частности:
- [math]\displaystyle{ {\color{blue}\sqrt[{\color{black}n}] {\color{black}{a}}} = a^{\frac{1}{n}} }[/math]
Попытки возведения в рациональную степень отрицательных чисел могут привести к ошибкам, поскольку значение алгебраического корня неоднозначно, а область значений арифметического корня ограничена неотрицательными числами. Пример возможной ошибки:
- [math]\displaystyle{ -1 = (-1)^{2\ \cdot\ \frac{1}{2}} = \left({(-1)^2}\right)^\frac{1}{2}=1^\frac{1}{2}={\color{blue}\sqrt{\color{black}1}}= 1 }[/math]
Функция корня
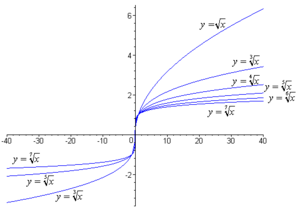
- Графики функций корня
-
Функции корня и обратные к ним степенные функции на интервале [math]\displaystyle{ [0; \ 1] }[/math]
-
Функции корня:
— арифметический, чётные степени 2, 4, 6
— общий, нечётные степени 3, 5, 7
Если рассматривать подкоренное выражение как переменную, мы получим функцию корня [math]\displaystyle{ n }[/math]-й степени: [math]\displaystyle{ y=\sqrt[n] x }[/math]. Функция корня относится к категории алгебраических функций. График любой функции корня проходит через начало координат и точку [math]\displaystyle{ (1; \ 1) }[/math].
Как сказано выше, для корня чётной степени, чтобы обеспечить однозначность функции, корень должен быть арифметическим, так что аргумент [math]\displaystyle{ x }[/math] неотрицателен. Функция корня нечётной степени однозначна и существует для любого вещественного значения аргумента.
| Тип функции корня | Область определения | Область значений | Другие свойства |
|---|---|---|---|
| Чётной степени | [math]\displaystyle{ [0; \ +\infty ) }[/math] | [math]\displaystyle{ [0; \ +\infty ) }[/math] | Функция выпукла вверх на всей области определения |
| Нечётной степени | [math]\displaystyle{ (-\infty; +\infty) }[/math] | [math]\displaystyle{ (-\infty; +\infty) }[/math] | Функция нечётна |
Для любой степени функция корня строго возрастает, непрерывна всюду внутри своей области определения. Неограниченно дифференцируема всюду, кроме начала координат, где производная обращается в бесконечность[11] [12]. Производная определяется по формуле[13]:
- [math]\displaystyle{ \frac {d}{dx} \sqrt[n]{x} = \frac {1} {n\sqrt[n]{x^{n-1}}} }[/math] . В частности, [math]\displaystyle{ \frac {d}{dx} \sqrt{x} = \frac {1} {2\sqrt{x}} }[/math].
Функция неограниченно интегрируема во всей области определения. Неопределенный интеграл ищется по формуле:
- [math]\displaystyle{ \int \sqrt[n]{x} \;dx = \frac{\sqrt[n]{x^{n+1}}}{1+\frac{1}{n}} + C }[/math] . В частности, [math]\displaystyle{ \int \sqrt{x} \;dx = \frac{2 \sqrt{x^3}}{3} + C }[/math] , где [math]\displaystyle{ C }[/math] — произвольная постоянная.
- Формула нахождения производной [math]\displaystyle{ k }[/math]-го порядка[14] функции [math]\displaystyle{ \sqrt[n]{x} }[/math]:
| [math]\displaystyle{ \frac {d^k}{dx^k} \sqrt[n]{x} = (-1)^{k} \frac {\prod^{k-1}_{m=0}(mn-1)}{{n^k}{\sqrt[n]{x^{kn-1}}}} }[/math] |
| где [math]\displaystyle{ \ k, n \in \mathbb {N}, \ x \ne 0 }[/math] |
- Формула нахождения [math]\displaystyle{ k }[/math]-го неопределённого интеграла[15] функции [math]\displaystyle{ \sqrt[n]{x} }[/math]:
| [math]\displaystyle{ \underbrace {\int\cdots\int}_{k} \sqrt[n]{x} \ \underbrace {dx\cdots dx}_{k} = \frac {{n^k}{\sqrt[n]{x^{kn+1}}}}{\prod^{k}_{m=1}(1+mn)} + C }[/math] |
| где [math]\displaystyle{ k, n \in \mathbb {N}, \ C=const }[/math] |
- Правые части формул являются алгебраическими выражениями, которые существуют всегда, при натуральном [math]\displaystyle{ k }[/math]. Следовательно и левые тоже.
Предельные соотношения
Приведём несколько полезных пределов, содержащих корни[16].
- [math]\displaystyle{ \lim_{n \to \infty} \sqrt[n]n = \lim_{n \to \infty} \sqrt[n]{\ln n} = 1 }[/math]
- [math]\displaystyle{ \lim_{n \to \infty} n \left(\sqrt[n]x -1 \right) = \lim_{n \to \infty} n \left(1-\frac{1}{\sqrt[n]{x}}\right)= \ln x }[/math]
- [math]\displaystyle{ \lim_{x \to 0} \frac{\sqrt[n]{(x+1)^m}-1}{x} = \frac{m}{n} }[/math]
- [math]\displaystyle{ \lim_{n \to \infty} \left(\frac{\sqrt[n]a+\sqrt[n]b}{2}\right)^n = \sqrt{ab} }[/math]
Практическое вычисление корней
Функция вычисления квадратных и кубических корней предусмотрена во многих калькуляторах; например, калькулятор Windows показывает соответствующие кнопки в режиме «Инженерный» (Научный). Если на электронном калькуляторе есть клавиша возведения в степень: [math]\displaystyle{ y^x, }[/math] то для извлечения корня из текущего числа надо нажать следующие клавиши[17].
- [math]\displaystyle{ y^x }[/math]
- Набрать показатель корня
- Нажать клавишу [math]\displaystyle{ 1/x }[/math]
- Нажать клавишу [math]\displaystyle{ = }[/math]
Для расчёта вручную можно использовать быстро сходящийся метод, изложенный в статье «Алгоритм нахождения корня n-ной степени». Для степеней выше третьей можно использовать логарифмическое тождество:
- [math]\displaystyle{ \sqrt[n]{x} = a^\frac {\log_a (x)} n = e^\frac {\ln (x)} n }[/math]
Для извлечения корня надо найти логарифм подкоренного выражения, разделить на степень корня и найти антилогарифм результата.
Корни из комплексных чисел
Зарождение понятия комплексного числа исторически было связано с желанием «легализовать» квадратные корни из отрицательных чисел. Как постепенно выяснилось, комплексные числа обладают богатыми алгебраическими и аналитическими свойствами; в частности, извлечение корней из них всегда возможно, хотя и неоднозначно. Для корней в комплексной области знак радикала обычно либо не используется, либо обозначает не функцию корня, а множество всех корней; в последнем случае, во избежание ошибок, знак радикала не должен использоваться в арифметических операциях. Пример возможной ошибки:
- [math]\displaystyle{ -1=(\sqrt{-1})^2 = \sqrt{(-1)^2}=\sqrt{1}=1 }[/math] (что, конечно, неверно)
Ошибка возникла из-за того, что неарифметический квадратный корень является многозначной функцией, и его нельзя использовать в арифметических действиях.
Способы нахождения
Запишем комплексное число [math]\displaystyle{ z }[/math] в тригонометрической форме:
- [math]\displaystyle{ z = r \left(\cos{\varphi} + i\sin{\varphi}\right) }[/math].
Тогда корни [math]\displaystyle{ n }[/math]-й степени из [math]\displaystyle{ z }[/math] определяются формулой Муавра (тригонометрическая форма)[18]:
- [math]\displaystyle{ \sqrt[n]{z} = {\color{blue}\sqrt[{\color{black}n}] {\color{black}{r}}}\left(\cos{\frac{\varphi+2\pi k}{n}} + i\sin{\frac{\varphi+2\pi k}{n}}\right),\;k = 0, 1, \dots, n-1 }[/math]
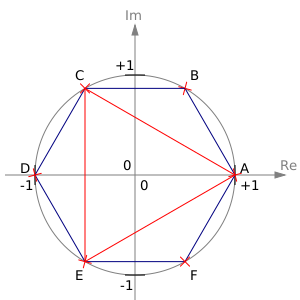
или в показательной форме:
- [math]\displaystyle{ z = r e^{i\varphi} }[/math] (См. Формула Эйлера)
- [math]\displaystyle{ \sqrt[n]{z} = {\color{blue}\sqrt[{\color{black}n}] {\color{black}{r}}}e^{\left(i\frac{\varphi+2\pi k}{n}\right)},\;k = 0, 1, \dots, n-1 }[/math]
Обозначения [math]\displaystyle{ z = x + iy, \ z \in \mathbb{C} }[/math] (комплексное число), |
Корень степени [math]\displaystyle{ n }[/math] из ненулевого комплексного числа имеет [math]\displaystyle{ n }[/math] значений (это следствие основной теоремы алгебры), и все они различны. Значение корня, получаемое при [math]\displaystyle{ k=0 }[/math], часто называется главным.
Поскольку для всех значений корня величина модуля одинакова (он определяется как арифметический корень из модуля изначального комплексного числа), а меняется лишь его аргумент, все [math]\displaystyle{ n }[/math] значений корня располагаются на комплексной плоскости на окружности радиуса [math]\displaystyle{ {\color{blue}\sqrt[{\color{black}n}] {\color{black}{r}}} }[/math] c центром в начале координат. Корни делят эту окружность на [math]\displaystyle{ n }[/math] равных частей.
Примеры
Найдём [math]\displaystyle{ \sqrt{-4} }[/math]. Поскольку [math]\displaystyle{ -4 = 4 (\cos{\pi} + i\sin{\pi}), }[/math] по формуле получаем:
- [math]\displaystyle{ \sqrt{-4} = 2 \left( \cos{\frac{\pi+2\pi k}{2}} + i\sin{\frac{\pi+2\pi k}{2}}\right),\;k = 0, 1 }[/math]
При [math]\displaystyle{ k=0 }[/math] получим первый корень [math]\displaystyle{ 2 i }[/math], при [math]\displaystyle{ k=1 }[/math] получим второй корень [math]\displaystyle{ (-2 i). }[/math]
Другой пример: найдём [math]\displaystyle{ \sqrt[4]{-16} }[/math]. Представим подкоренное выражение в тригонометрической форме:
- [math]\displaystyle{ -16 = 16\ (\cos(\pi + 2k\pi) + i \sin(\pi + 2k\pi) ) }[/math]
По формуле Муавра получаем:
- [math]\displaystyle{ z_k = \sqrt[4]{-16} = \sqrt[4]{16} \left( \cos\frac{\pi + 2k\pi}{4} + i \sin\frac{\pi + 2k\pi}{4} \right) }[/math]
В итоге имеем четыре значения корня[19]:
- [math]\displaystyle{ z_0=2 \left( \cos\frac{\pi}{4} + i \sin\frac{\pi}{4} \right) = \sqrt{2}\ (1+i) }[/math]
- [math]\displaystyle{ z_1=2 \left( \cos\frac{3\pi}{4} + i \sin\frac{3\pi}{4} \right) = \sqrt{2}\ (-1+i) }[/math]
- [math]\displaystyle{ z_2=2 \left( \cos\frac{5\pi}{4} + i \sin\frac{5\pi}{4} \right) = -\sqrt{2}\ (1+i) }[/math]
- [math]\displaystyle{ z_3=2 \left( \cos\frac{7\pi}{4} + i \sin\frac{7\pi}{4} \right) = \sqrt{2}\ (1-i) }[/math]
Можно записать сводный ответ в виде: [math]\displaystyle{ \sqrt[4]{-16} = \sqrt{2}\ (\pm 1 \pm i) }[/math]
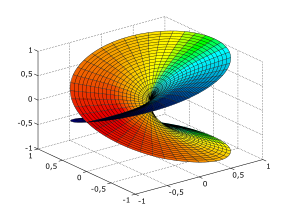
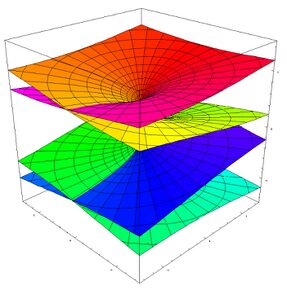
Комплексная функция корня и риманова поверхность
Рассмотрим комплексную функцию корня [math]\displaystyle{ n }[/math]-й степени: [math]\displaystyle{ w=\sqrt[n]{z}. }[/math] Согласно сказанному выше, эта функция является многозначной (точнее, [math]\displaystyle{ n }[/math]-значной) функцией, и это создаёт неудобства при её исследовании и применении. В комплексном анализе вместо рассмотрения многозначных функций на комплексной плоскости принято иное решение: рассматривать функцию как однозначную, но определённую не на плоскости, а на более сложном многообразии, которое называется римановой поверхностью[20].
-
Риманова поверхность для комплексного квадратного корня
-
Риманова поверхность для комплексного корня 4-й степени
Для комплексной функции корня [math]\displaystyle{ n }[/math]-й степени её риманова поверхность (см. рисунки) состоит из [math]\displaystyle{ n }[/math] ветвей (листов), связанных винтообразно, причём последний лист связан с первым. Эта поверхность непрерывна и односвязна. Один из листов содержит главные значения корня, получаемые как аналитическое продолжение вещественного корня с положительного луча вещественной оси.
Опишем для простоты комплексную функцию квадратного корня. Её риманова поверхность состоит из двух листов. Первый лист можно представить как комплексную плоскость, у которой вырезан положительный луч вещественной оси. Значения функции корня [math]\displaystyle{ w }[/math] на этом листе имеют вдвое меньший аргумент, чем [math]\displaystyle{ z }[/math], и поэтому они заполняют верхнюю часть комплексной плоскости значений. На разрезе первый лист склеен со вторым, и функция непрерывно продолжается через разрез на второй лист, где её значения заполняют нижнюю часть комплексной плоскости значений. Оставшиеся свободными начало первого листа и конец второго тоже склеим, после чего полученная функция на римановой поверхности становится однозначной и всюду непрерывной[20].
Единственный нуль у функции (первого порядка) получается при [math]\displaystyle{ z=0 }[/math]. Особые точки: [math]\displaystyle{ z=0 }[/math] и [math]\displaystyle{ z=\infty }[/math] (точки разветвления бесконечного порядка)[20]. Понятие точки разветвления означает, что замкнутый контур в окрестности нуля неизбежно содержит переход с листа на лист.
В силу односвязности риманова поверхность корня является универсальной накрывающей[21] для комплексной плоскости без точки [math]\displaystyle{ 0 }[/math].
Вариации и обобщения
Корень [math]\displaystyle{ n }[/math]-й степени из [math]\displaystyle{ a }[/math] есть решение уравнения [math]\displaystyle{ x^n=a }[/math], и его в принципе можно определить всюду, где такое уравнение имеет смысл. Чаще всего рассматривают такие обобщения в алгебраических кольцах. Лучше всего исследованы обобщённые квадратные корни.
Если кольцо есть область целостности, то квадратных корней из ненулевого элемента может быть либо два, либо ни одного. В самом деле, если имеются два корня [math]\displaystyle{ a, b, }[/math] то [math]\displaystyle{ a^2=b^2, }[/math] откуда: [math]\displaystyle{ (a-b)(a+b)=0 }[/math], то есть, в силу отсутствия делителей нуля, [math]\displaystyle{ a=\pm b }[/math]. В более общем случае, когда в кольце имеются делители нуля или оно некоммутативно, число корней может быть любым.
В теории чисел рассматривается конечное кольцо вычетов по модулю [math]\displaystyle{ m }[/math]: если сравнение [math]\displaystyle{ x^n \equiv a \pmod m }[/math] имеет решение, то целое число [math]\displaystyle{ a }[/math] называется вычетом степени n (в противном случае — невычетом степени n). Решение [math]\displaystyle{ x }[/math], если оно существует, является полным аналогом корня n-й степени из целого числа [math]\displaystyle{ a }[/math]. Чаще всего используются случаи[22]:
- [math]\displaystyle{ n=2 }[/math] (квадратичные вычеты)
- [math]\displaystyle{ n=3 }[/math] (кубические вычеты)
- [math]\displaystyle{ n=4 }[/math] (биквадратичные вычеты)
Корни для кватернионов имеют много общего с комплексными, но есть и существенные особенности. Квадратный кватернионный корень обычно имеет 2 значения, но если подкоренное выражение — отрицательное вещественное число, то значений бесконечно много. Например, квадратные корни из [math]\displaystyle{ -1 }[/math] образуют трёхмерную сферу, определяемую формулой[23]:
- [math]\displaystyle{ \{ai + bj + ck \mid a^2 + b^2 + c^2 = 1\} \,. }[/math]
Для кольца квадратных матриц доказано, что если матрица положительно определена, то положительно определённый квадратный корень из матрицы существует и единственен[24]. Для матриц других типов корней может быть сколько угодно (в том числе ни одного).
Квадратные корни вводятся также для функций[25], операторов[26] и других математических объектов.
История
Развитие понятия

[math]\displaystyle{ = 1{,}41421296\dots }[/math]
Первые задачи, связанные с извлечением квадратного корня, обнаружены в трудах вавилонских математиков (о достижениях древнего Египта в этом отношении ничего не известно). Среди таких задач[27]:
- Применение теоремы Пифагора для нахождения стороны прямоугольного треугольника по известным двум другим сторонам.
- Нахождение стороны квадрата, площадь которого задана.
- Решение квадратных уравнений.
Вавилонские математики (II тысячелетие до н. э.) разработали для извлечения квадратного корня особый численный метод. Начальное приближение для [math]\displaystyle{ \sqrt{a} }[/math] рассчитывалось исходя из ближайшего к корню (в меньшую сторону) натурального числа [math]\displaystyle{ n }[/math]. Представив подкоренное выражение в виде: [math]\displaystyle{ a=n^2+r }[/math], получаем: [math]\displaystyle{ x_0=n+\frac{r}{2n} }[/math], затем применялся итеративный процесс уточнения, соответствующий методу Ньютона[28]:
- [math]\displaystyle{ x_{n+1}=\frac{1}{2}~\left(x_n + \frac{a}{x_n}\right)\ }[/math]
Итерации в этом методе очень быстро сходятся. Для [math]\displaystyle{ \sqrt{5} }[/math], например, [math]\displaystyle{ a=5;\;n=2;\;r=1;\ x_0=\frac{9}{4} = 2{,}25, }[/math] и мы получаем последовательность приближений:
- [math]\displaystyle{ x_1=\frac{161}{72} = 2{,}23611;\; x_2=\frac{51841}{23184} = 2{,}2360679779 }[/math]
В заключительном значении верны все цифры, кроме последней.
Аналогичные задачи и методы встречаются в древнекитайской «Математике в девяти книгах»[29]. Древние греки сделали важное открытие: [math]\displaystyle{ \sqrt{2} }[/math] — иррациональное число. Детальное исследование, выполненное Теэтетом Афинским (IV век до н. э.), показало, что если корень из натурального числа не извлекается нацело, то его значение иррационально[30].
Греки сформулировали проблему удвоения куба, которая сводилась к построению кубического корня с помощью циркуля и линейки. Проблема оказалась неразрешимой. Численные алгоритмы извлечения кубического корня опубликовали Герон (в трактате «Метрика», I век н. э.) и индийский математик Ариабхата I (V век)[31].
Алгоритмы извлечения корней любой степени из целого числа, разработанные индийскими и исламскими математиками, были усовершенствованы в средневековой Европе. Николай Орем (XIV век) впервые истолковал[32] корень [math]\displaystyle{ n }[/math]-й степени как возведение в степень [math]\displaystyle{ \frac{1}{n} }[/math].
После появления формулы Кардано (XVI век) началось применение в математике мнимых чисел, понимаемых как квадратные корни из отрицательных чисел[33]. Основы техники работы с комплексными числами разработал в XVI веке Рафаэль Бомбелли, который также предложил оригинальный метод вычисления корней (с помощью цепных дробей). Открытие формулы Муавра (1707) показало, что извлечение корня любой степени из комплексного числа всегда возможно и не приводит к новому типу чисел[34].
Комплексные корни произвольной степени в начале XIX века глубоко исследовал Гаусс, хотя первые результаты принадлежат Эйлеру[35]. Чрезвычайно важным открытием (Галуа) стало доказательство того факта, что не все алгебраические числа (корни многочленов) могут быть получены из натуральных с помощью четырёх действий арифметики и извлечения корня[36].
Этимология термина и происхождение символики
Термин корень имеет долгую и сложную историю. Извлечение квадратного корня древние греки понимали строго геометрически: как нахождение стороны квадрата по известной его площади. После перевода на санскрит греческое слово «сторона» превратилась в «мула» (основание). Слово «мула» имело также значение «корень», поэтому при переводе индийских сиддхант на арабский использовался термин «джизр» (корень растения). Впоследствии аналогичное по смыслу слово «radix» закрепилось в латинских переводах с арабского, а через них и в русской математической терминологии («корень», «радикал»)[37].
Средневековые математики (например, Кардано) обозначали квадратный корень[38] символом Rx, сокращение от слова «radix». Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов (то есть алгебраистов), в 1525 году[39]. Происходит этот символ от стилизованной первой буквы того же слова «radix». Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт (1637) для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня.
Показатель степени появился в знаке корня благодаря Валлису и «Универсальной арифметике» Ньютона (XVIII век)[40].
См. также
- Алгоритм нахождения корня n-ной степени
- Возведение в степень
- Квадратный корень
- Корни из единицы
- Кубический корень
- Логарифм
- Основная теорема алгебры
- Степенная функция
Литература
- Выгодский М. Я. Справочник по элементарной математике. — изд. 25-е. — М.: Наука, 1978. — ISBN 5-17-009554-6.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- История математики, в трёх томах / Под редакцией А. П. Юшкевича. — М.: Наука, 1970—1972.
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — 2-е изд. — М.: Наука, 1970. — 720 с.
- Мордкович А. Г. Алгебра и начала анализа. Учебник для 10—11 классов, часть 1. — изд. 4-е. — М.: Мнемозина, 2003. — 376 с.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.
Примечания
- ↑ Корень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Перейти обратно: 2,0 2,1 Элементарная математика, 1976, с. 49.
- ↑ Корн Г., Корн Т. Справочник по математике, 1970, с. 33.
- ↑ Сканави М. И. Элементарная математика. П. 1.11. С. 49.
- ↑ Перейти обратно: 5,0 5,1 Выгодский М. Я. Справочник по элементарной математике, 1978, с. 64.
- ↑ Арифметический корень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 1.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Т. I, С. 35—36.
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 141—143.
- ↑ Алгебра и начала анализа. Учебник для 10—11 классов, под ред. А. Н. Колмогорова. М.: Просвещение, 2002, С. 209.
- ↑ Перейти обратно: 10,0 10,1 Выгодский М. Я. Справочник по элементарной математике, 1978, с. 183.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Т. I, С. 194, 198.
- ↑ Мордкович А. Г., 2003, с. 236—238.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Т. I, С. 215.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Т. I, С. 233, частный случай для [math]\displaystyle{ \mu=\frac{1}{n}. }[/math].
- ↑ Не путать с кратными интегралами. Их записи весьма похожи, но [math]\displaystyle{ k }[/math]-й интеграл является неопределённым, в то время как [math]\displaystyle{ k }[/math]-кратный интеграл — определённый.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 67, 131—132, 164, 166—167.
- ↑ Алгебра. 9 класс. Учебник для общеобразовательных учреждений / Под ред. С. А. Теляковского. — Изд. 18-е. — М.: Просвещение, 2011. — С. 53. — ISBN 978-5-09-025168-6.
- ↑ Корн Г., Корн Т. Справочник по математике, 1970, с. 36—37.
- ↑ Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — издание третье, стереотипное. — М.: Наука, 1976. — С. 68. — 591 с.
- ↑ Перейти обратно: 20,0 20,1 20,2 Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967, с. 96-99, 28—29.
- ↑ Болтянский В. Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982. — С. 112. — (Библиотечка Квант, выпуск 21).
- ↑ Виноградов И. М. Основы теории чисел. — М.—Л.: ГИТТЛ, 1952. — С. 71. — 180 с.
- ↑ Porteous, Ian R. Clifford Algebras and the Classical Groups. Cambridge, 1995, page 60.
- ↑ См., например: Гантмахер Ф. Р. Теория матриц. М.: ГИТТЛ, 1953, С. 212—219, или: Воеводин В., Воеводин В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. Спб.: БХВ-Петербург, 2006.
- ↑ См., например: Ершов Л. В., Райхмист Р. Б. Построение графиков функций. М.: Просвещение, 1984, или: Каплан И. А. Практические занятия по высшей математике. Харьков: Изд-во ХГУ, 1966.
- ↑ См., например: Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. М.: Мир, 1983, или: Халмош П. Гильбертово пространство в задачах. М.: Мир, 1970.
- ↑ История математики, 1970—1972, Том I, С. 42—46.
- ↑ История математики, 1970—1972, Том I, С. 47.
- ↑ История математики, 1970—1972, Том I, С. 169—171.
- ↑ Башмакова И. Г. Становление алгебры (из истории математических идей). — М.: Знание, 1979. — С. 23. — (Новое в жизни, науке, технике. Математика, кибернетика, № 9).
- ↑ Abhishek Parakh. Ariabhata's root extraction methods // Indian Journal of History of Science. — 2007. — Вып. 42.2. — С. 149—161. Архивировано 9 июня 2010 года.
- ↑ История математики, 1970—1972, Том I, С. 275—276.
- ↑ История математики, 1970—1972, Том I, С. 296—298.
- ↑ История математики, 1970—1972, Том III, С. 56—59.
- ↑ История математики, 1970—1972, Том III, С. 62.
- ↑ Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Математическая логика, алгебра, теория чисел, теория вероятностей. — М.: Наука, 1978. — Т. I. — С. 58—66.
- ↑ История математики, 1970—1972, Том I, С. 185.
- ↑ Никифоровский В. А. Из истории алгебры XVI-XVII вв. — М.: Наука, 1979. — С. 81. — 208 с. — (История науки и техники).
- ↑ Знаки математические // Математическая энциклопедия. — М.: Советская Энциклопедия, 1982. — Т. 2.
- ↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник, изд. 3-е. — СПб.: ЛКИ, 2008. — С. 82. — 248 с. — ISBN 978-5-382-00839-4.
![Функции корня и обратные к ним степенные функции на интервале [math]\displaystyle{ [0; \ 1] }[/math]](https://cdn.xn--h1ajim.xn--p1ai/thumb.php?f=Funci%C3%B3n_ra%C3%ADz_1.png&width=297)