Многозначная функция

Функция от элемента «3» принимает два значения

Многозна́чная фу́нкция — обобщение понятия функции, допускающее наличие нескольких значений функции для одного аргумента.

Определение

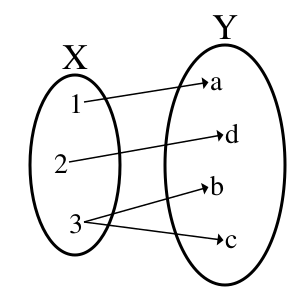
Функция [math]\displaystyle{ F }[/math], которая каждому элементу множества [math]\displaystyle{ X }[/math] ставит в соответствие некоторое подмножество множества [math]\displaystyle{ Y, }[/math] называется многозначной функцией, если хотя бы для одного [math]\displaystyle{ x \in X }[/math] значение [math]\displaystyle{ F(x) }[/math] содержит более одного элемента [math]\displaystyle{ Y. }[/math]

Обычные (однозначные) функции можно рассматривать как частный случай многозначных, у которых значение состоит ровно из одного элемента.

Примеры

Простейший пример — двузначная функция квадратного корня из положительного числа, у неё два значения, различающиеся знаком. Например, квадратный корень из 16 имеет два значения — [math]\displaystyle{ +4 }[/math] и [math]\displaystyle{ -4. }[/math]

Другой пример — обратные тригонометрические функции (например, арксинус) — поскольку значения прямых тригонометрических функций повторяются с периодом [math]\displaystyle{ 2\pi }[/math] или [math]\displaystyle{ \pi, }[/math] то значения обратных функций многозначны («бесконечнозначны»), все они имеют вид [math]\displaystyle{ \varphi+2k\pi }[/math] или [math]\displaystyle{ \varphi+k\pi, }[/math] где [math]\displaystyle{ k }[/math] — произвольное целое число.

Многозначные функции неудобно использовать в формулах, поэтому из их значений нередко выделяют одно, которое называют главным. Для квадратного корня это неотрицательное значение, для арксинуса — значение, попадающее в интервал [math]\displaystyle{ \left[-\frac{\pi}{2}, \frac{\pi}{2}\right] }[/math] и т. д.

Первообразную функцию (неопределённый интеграл) также можно рассматривать как бесконечнозначную функцию, поскольку она определена с точностью до константы интегрирования.

В комплексном анализе и алгебре

Характерный пример многозначных функций — некоторые аналитические функции в комплексном анализе. Неоднозначность возникает при аналитическом продолжении по разным путям. Также часто многозначные функции получаются в результате взятия обратных функций.

Например, корень n-ой степени из любого ненулевого комплексного числа принимает ровно [math]\displaystyle{ n }[/math] значений. У комплексного логарифма число значений бесконечно, одно из них объявлено главным.

В комплексном анализе понятие многозначной функции тесно связано с понятием римановой поверхности — поверхности в многомерном комплексном пространстве, на которой данная функция становится однозначной.

См. также

• Многозначное отображение

Литература

• Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — 4-е изд.. — М.: Наука, 1972.
• Шабат Б. В. Введение в комплексный анализ. — М.: Наука, 1969. — 577 с.