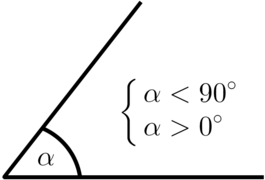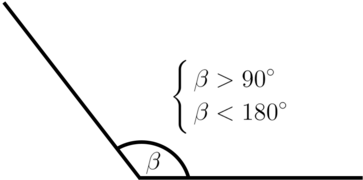Угол

Угол
Угол
	Файл:∠
Размерность	безразмерная
Единицы измерения
СИ	радиан
Другие единицы	градус, минута, секунда, град, тысячная

У́гол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла)^[1].

Общие сведения

Плоскость, содержащая обе стороны угла, делится углом на две области. Каждая из этих областей, объединённая со сторонами угла, называется плоским углом (или просто углом, если это не вызывает разночтений). Один из плоских углов (обычно меньший из двух) иногда условно называют внутренним, а другой — внешним. Точки плоского угла, не принадлежащие его сторонам, образуют внутреннюю область плоского угла.

В другом, эквивалентном варианте определения плоским углом называется часть плоскости, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую лежащую в этой плоскости линию (которая называется линией, стягивающей данный плоский угол).

Часто для краткости углом называют также угловую меру, то есть число, определяющее величину угла.

Кроме наиболее часто встречающихся плоских углов, в качестве углов могут рассматриваться и более общие объекты — фигуры, образованные пересекающимися дугами, полуплоскостями и другими фигурами как в евклидовой, так и в других типах геометрии в метрических пространствах различной размерности.

Обозначение углов

Для обозначения угла имеется общепринятый символ: [math]\displaystyle{ \angle , }[/math] предложенный в 1634 году французским математиком Пьером Эригоном. Символ содержится в Юникоде (U+2220 ∠ angle).

В математических выражениях углы часто обозначают строчными греческими буквами: α, β, γ, θ, φ и др. Как правило, данные обозначения также наносятся на чертёж для устранения неоднозначности в выборе внутренней области угла. Чтобы избежать путаницы с числом пи, символ π, как правило, для этой цели не используется. Для обозначения телесных углов (см. ниже) часто применяют буквы ω и Ω.

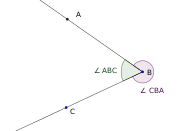
Также часто угол обозначают тремя символами точек, например [math]\displaystyle{ \angle ABC. }[/math] В такой записи [math]\displaystyle{ B }[/math] — вершина, а [math]\displaystyle{ A }[/math] и [math]\displaystyle{ C }[/math] — точки, лежащие на разных сторонах угла. В связи с выбором в математике направления отсчёта углов против часовой стрелки, точки, лежащие на сторонах в обозначении угла принято перечислять также против часовой стрелки. Это соглашение позволяет обеспечить однозначность при различении двух плоских углов с общими сторонами, но различными внутренними областями. В тех случаях, когда выбор внутренней области плоского угла ясен из контекста, либо указывается другим способом, данное соглашение может нарушаться. См. вариации и обобщения.

Реже используются обозначения прямых, образующих стороны угла. Например, [math]\displaystyle{ \angle(bc) }[/math] — здесь предполагается, что имеется в виду внутренний угол треугольника [math]\displaystyle{ \angle BAC }[/math], α, который надо было бы обозначить [math]\displaystyle{ \angle(cb) }[/math].

Так, для рисунка справа записи γ, [math]\displaystyle{ \angle ACB }[/math] и [math]\displaystyle{ \angle(ba) }[/math] означают один и тот же угол.

Иногда для обозначения углов используются строчные латинские буквы (a, b, c, …) и цифры.

На чертежах углы отмечаются небольшими одинарными, двойными или тройными дужками, проходящими по внутренней области угла с центрами в вершине угла. Равенство углов может отмечаться одинаковой кратностью дужек или одинаковым количеством поперечных штрихов на дужке. Если необходимо указать направление отсчёта угла, оно отмечается стрелкой на дужке. Прямые углы отмечаются не дужками, а двумя соединёнными равными отрезками, расположенными таким образом, что вместе со сторонами они образуют небольшой квадрат, одна из вершин которого совпадает с вершиной угла.

Угловая мера

Угловая мера, позволяющая сравнивать плоские углы, может быть введена следующим образом. Два плоских угла называются равными (или конгруэнтными), если они могут быть совмещены так, что совпадут их вершины и обе стороны. От любого луча на плоскости в данную сторону можно отложить единственный угол, равный данному. Если один угол может быть размещён полностью внутри другого угла таким образом, что вершина и одна из сторон этих углов совпадают, то первый угол меньше второго. Назовём прилежащими два угла, расположенные так, что сторона одного совпадает со стороной другого (а значит, совпадают и вершины), но их внутренние области не пересекаются. Угол, составленный из несовпадающих сторон двух прилежащих углов, назовём сложенным из этих углов. Каждому углу можно поставить в соответствие число (угловую меру) таким образом, что:

равным углам соответствует равная угловая мера;
меньшему углу соответствует меньшая угловая мера;
у угла, стороны которого совпадают (нулевого угла), угловая мера равна нулю (то же справедливо и для угла между параллельными прямыми);
каждый ненулевой угол имеет определённую угловую меру, большую нуля;
(аддитивность) угловая мера угла равна сумме угловых мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

В некоторых системах обозначений, если есть необходимость различать угол и его меру, для угла (геометрической фигуры) используют обозначение [math]\displaystyle{ \angle ABC , }[/math] а для величины меры измерения этого угла — обозначение [math]\displaystyle{ \widehat{ ABC}. }[/math]

Угол измеряют:

Наиболее распространённая градусная мера — градус, минута, секунда, в которой за 1° принимается 1/180 от развёрнутого угла (см. ниже), одна минута [math]\displaystyle{ 1'=1^\circ/60 }[/math], и одна секунда [math]\displaystyle{ 1''=1'/60 }[/math]. Градусная мера применяется в элементарной геометрии (измерение углов на чертежах транспортиром), в геодезии по карте и на местности (для измерения углов на местности используют весьма точный прибор — универсал/теодолит).

Радианная мера угла — отношение длины s стягивающей дуги к её радиусу r. Радианная мера используется в математическом анализе (например, как числовой аргумент тригонометрических функций и при определении числовых (табличных и графических) значений обратных аркфункций), в планиметрии и механике (при рассмотрении вращения около точки или оси и других процессов, описываемых с помощью тригонометрических функций, — колебаний, волн и так далее).

Углы можно измерять также в оборотах. Один оборот — это полный угол (то есть угол в 360 градусов). Про произвольный угол говорят, что он составляет x оборотов, если x — отношение длины s дуги, стягивающей угол, к длине L окружности, содержащей эту дугу.

Градовая мера измерения углов была предложена к применению исторически, в настоящее время почти нигде не используется, поскольку не вытеснила более распространённую шестидесятеричную градусную.

Измерение углов в градусной мере восходит к Древнему Вавилону, где использовалась шестидесятеричная система счисления, следы которой сохранились у нас в делении времени и углов. Один градус (1/360 полного угла) делится на 60 угловых минут (или минут дуги), в свою очередь минута делится на 60 угловых секунд (секунд дуги). Меньшие углы измеряются в дольных единицах секунды, образуемыми с помощью приставок СИ (угловая миллисекунда, угловая микросекунда и т.д.).

1 оборот = 2π радианам = 360° = 400 градам.

В системе СИ основной единицей измерения угла является радиан.

В морской терминологии углы измеряются в румбах. 1 румб равен ¹⁄₃₂ от полной окружности (360 градусов) компаса, то есть 11,25 градуса, или 11°15′.

В астрономии угол прямого восхождения и часовой угол в экваториальной системе координат измеряются в часах, минутах и секундах (составляющих соответственно ¹⁄₂₄, ¹⁄₁₄₄₀ и ¹⁄_86 400 полной окружности); это связано с угловой скоростью осевого вращения Земли, составляющей приблизительно 1 оборот за 24 часа^[2]. Таким образом, за один час (минуту, секунду) времени небесная сфера «поворачивается» примерно на 1 час (минуту, секунду) в угловой мере. Остальные угловые величины в астрономии выражаются обычно в градусах, минутах и секундах дуги. Одна секунда (минута) прямого восхождения равна 15 секундам (минутам) дуги.

В артиллерии и оружейном деле используются также тысячные и деления угломера.

В некоторых контекстах, таких как идентификация точки в полярных координатах или описание ориентации объекта в двух измерениях относительно его базовой ориентации, углы, отличающиеся на целое число полных оборотов, фактически являются эквивалентными. Например, в таких случаях можно считать эквивалентными углы 15° и 360015° (= 15° + 360°×1000). В других контекстах, таких как идентификация точки на спиральной кривой или описание совокупного вращения объекта в двух измерениях относительно его начальной ориентации, углы, отличающиеся на ненулевое целое число полных оборотов, не эквивалентны.

Некоторые плоские углы имеют специальные названия. Кроме вышеназванных единиц измерения (радиан, румб, градус и тому подобное), к ним относятся:

квадрант (прямой угол, ¹⁄₄ окружности);
секстант (¹⁄₆ окружности);
октант (¹⁄₈ окружности; кроме того, в стереометрии октантом называется трёхгранный угол, образованный тремя взаимно перпендикулярными плоскостями),

Иногда углы (например, угол уклона поверхности) измеряют не собственно угловой мерой, а её тангенсом (или синусом), то есть отношением подъёма по наклонной плоскости к проекции на горизонталь пройденного по ней пути (или к самому этому пути). Для обычного случая малых углов уклона это отношение примерно равно углу, выраженному в радианах (tg α ≈ sin α ≈ α, при α < 0,1 разница между этими величинами менее 1 %). При этом отношение выражается обычно в процентах или промилле. Например, уклон дороги в 10 % означает, что на каждые 100 метров пути (в проекции на горизонталь) дорога поднимается на 10 м; угол к горизонту равен arctg(10/100) ≈ 5,71° ≈ 0,1 радиана. Такой способ измерения углов не является, строго говоря, угловой мерой, так как не обладает свойством аддитивности (см. выше). См. также приближения для малых углов^[англ.].

Направление отсчёта углов

В математике и физике, обычно, положительным направлением отсчёта углов считается направление против часовой стрелки. Обычно, угол начинают измерять от луча, начало которого совпадает с центром системы координат (СК), а направление совпадает с положительным направлением оси абсцисс (в полярной СК, цилиндрической СК, сферической СК, СК на тригонометрической окружности и других).

В географии и геодезии за начало отсчёта углов по азимуту принято направление «на север»; угол отсчитывается по часовой стрелке. Таким образом, направлению «на восток» соответствует азимутальный угол 90°, «на юг» — 180°, «на запад» — 270°. В артиллерии предпочитают направление полярной оси «на юг» и соответствующий полярный угол называют также азимутом (направление «на запад» соответствует азимутальному углу 90°).

Типы углов

Выпуклый угол
Прямой угол
Полный угол
Острый угол
Тупой угол
Развёрнутый угол

В зависимости от величины углы называются следующим образом.

Нулевой угол (0°); стороны нулевого угла совпадают, его внутренняя область — пустое множество.
Острый угол (от 0° до 90°, не включая граничные значения).
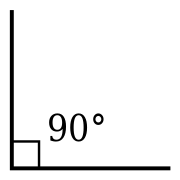
Прямой угол (90°); стороны прямого угла перпендикулярны друг другу.
Тупой угол (от 90° до 180°, не включая граничные значения).
Косой угол (любой, не равный 0°, 90°, 180° или 270°).
Развёрнутый угол (180°); сторонами развёрнутого угла являются две полупрямые одной прямой, то есть два луча, направленных в противоположные стороны.
Невыпуклый угол (от 0° до 180° включительно).
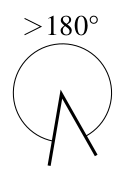
Выпуклый угол (от 180° до 360°, не включая граничные значения).
Полный угол (360°) — см. оборот (единица измерения).

Биссектриса

Биссектрисой (от лат. bi- «двойное» и sectio «разрезание») угла называется луч, выходящий из вершины угла и проходящий через его внутреннюю область, который образует с его сторонами два равных угла. Расстояние любой точки биссектрисы от сторон угла одинаково (и, обратно, любая точка внутренней области угла, равноудалённая от сторон угла, лежит на его биссектрисе).

Плоские углы

Термин плоский угол употребляется как синоним термина угол, определённого в начале статьи, для отличия его от употребляемого в стереометрии понятия телесного угла (в том числе двугранного, трёхгранного или многогранного угла).

Под свойствами плоских углов нередко понимают соотношения величин углов (смежных, дополнительных, прилегающих, вертикальных — см. ниже) в случае, когда углы лежат в одной плоскости (для планиметрии это подразумевается само собой, однако для стереометрии уточнение необходимо, иначе перечисленные ниже соотношения не имеют места, а сами углы, если не лежат в одной плоскости, не называются смежными или прилегающими (вертикальные всегда лежат в одной плоскости автоматически).

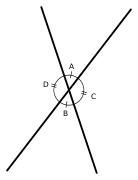
Вертикальные и прилежащие углы

Вертикальные углы. Две пары углов (A и B, C и D) попарно равны
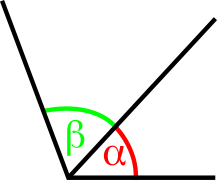
Прилежащие углы. Величина угла, образованного внешними (не общими) их сторонами, равна сумме величин их самих (α + β)
Дополнительные углы a и b (взаимно дополняют друг друга до прямого угла). Оба дополнительных угла являются острыми
Смежные углы — на этом рисунке острый (α) и тупой (β) — образуют развёрнутый угол (α + β)
Сопряжённые углы — образуют полный угол (360°); на этом рисунке частный пример: 150° + 210° = 360°

Вертикальные углы — 2 угла на плоскости, которые образуются при пересечении 2 непараллельных прямых. Эти 2 угла не имеют общих сторон (то есть, стороны одного угла являются продолжением сторон другого). Их основное свойство: вертикальные углы равны.
Прилежащие углы — 2 угла на 1 плоскости, имеющие общими по 1 вершине и по 1 из 2 сторон, но не пересекающиеся внутренними областями. Величина угла, образованного 2 внешними (не общими) сторонами прилежащих углов, равна сумме величин самих прилежащих углов (на рисунке α + β).

Частные случаи прилежащих углов.

Если прилежащие углы равны, то их общая сторона — биссектриса.

Дополнительные углы — два угла с общей вершиной на плоскости, одна из сторон которых — общая, а оставшиеся стороны составляют прямой угол. Сумма дополнительных углов равна 90°. Синус, тангенс и секанс угла равны соответственно косинусу, котангенсу и косекансу дополнительного угла.

Смежные углы — 2 угла с 1 общей вершиной на плоскости, 1 из 2 сторон которых — общая, а оставшиеся 2 стороны лежат на 1 прямой (не совпадая). Сумма 2 смежных углов равна 180°. То есть, 2 смежных угла на плоскости это — 2 прилежащих угла, дающих в сумме 180°.

Сопряжённые углы — 2 угла на плоскости, имеющие общими 1 вершину и 2 стороны, по которым они примыкают (граничат) друг к другу, но различаются внутренними областями; объединение таких 2 углов представляет собой всю плоскость, а, как прилежащие углы, они образуют в сумме полный угол; сумма их величин равна 360°.

Плоские углы с (анти)параллельными сторонами

Углы, стороны которых попарно параллельны и сонаправлены (или попарно параллельны и противоположно направлены), равны друг другу. Пара углов, у которых одна пара сторон параллельна и сонаправлена друг другу, а вторая пара сторон параллельна и противоположно направлена, составляют в сумме по величине развёрнутый угол, то 180° (см. рисунок) — поскольку их можно параллельным переносом превратить в смежные углы («склеив» сонаправленные стороны).

Углы со взаимно перпендикулярными сторонами

Два угла со взаимно перпендикулярными сторонами равны, если оба они острые или оба тупые.

Внешний угол треугольника

Теорема о внешнем угле треугольника. Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с внешним углом.

Углы многоугольника

Сумма внутренних углов α_i произвольного n-угольника без самопересечений равна [math]\displaystyle{ \sum_{i=1}^n \alpha_i = (n-2)\cdot 180^{\circ} . }[/math]

Так,

сумма внутренних углов треугольника равна 180°,
четырёхугольника — 360°,
пятиугольника — 540° и так далее.

Следствие

Назовём внешним углом β_i (внимание, это не обычное определение внешнего угла) угол, дополняющий внутренний угол α_i до полного угла: β_i = 360° − α_i.

Сумма внешних углов произвольного n-угольника без самопересечений равна [math]\displaystyle{ \sum_{i=1}^n \beta_i = n\cdot 360^{\circ} - \sum_{i=1}^n \alpha_i = (n+2)\cdot 180^{\circ} . }[/math]

Центральный и вписанный угол

Любой конкретной дуге окружности можно сопоставить единственный центральный и бесконечное множество вписанных углов.

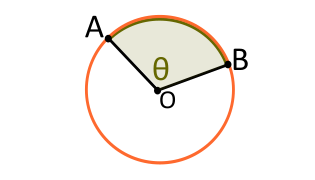
Центральный угол
Вписанный угол

Центральный угол — угол с вершиной в центре окружности. Величина центрального угла равна градусной мере дуги, заключённой между сторонами этого угла.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Величина вписанного угла равна половине градусной меры дуги, ограниченной его сторонами. Все вписанные углы, опирающиеся на одну и ту же дугу, равны.

Величина вписанного угла равна половине величины центрального угла, опирающегося у основания на окружности на ту же самую дугу (см. рис.).

Вариации и обобщения

Величиной ориентированного угла между прямыми [math]\displaystyle{ AB }[/math] и [math]\displaystyle{ CD }[/math] (обозначение: [math]\displaystyle{ \angle(AB,CD) }[/math]) называют величину угла, на который нужно повернуть против часовой стрелки прямую [math]\displaystyle{ AB }[/math] так, чтобы она стала параллельна прямой [math]\displaystyle{ CD. }[/math] При этом углы, отличающиеся на n·180° (n — целое число), считаются равными. Ориентированный угол между прямыми [math]\displaystyle{ CD }[/math] и [math]\displaystyle{ AB }[/math] не равен ориентированному углу между прямыми [math]\displaystyle{ AB }[/math] и [math]\displaystyle{ CD }[/math] (они составляют в сумме 180° или, что по соглашению то же самое, 0°). Ориентированные углы обладают следующими свойствами: а) [math]\displaystyle{ \angle(AB,BC)=-\angle(BC,AB); }[/math] б) [math]\displaystyle{ \angle(AB,CD)+\angle(CD,EF)=\angle(AB,EF); }[/math] в) точки [math]\displaystyle{ A,B,C,D, }[/math] не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда [math]\displaystyle{ \angle(AB,BC)=\angle(AD,DC). }[/math]

Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла, расширив его область определения на всю числовую прямую [math]\displaystyle{ (-\infty ; +\infty) }[/math]: вводятся углы, большие 360°, в зависимости от направления вращения различают положительные и отрицательные углы. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.

Понятие угла обобщается на рассматриваемый в стереометрии телесный угол.

Телесный угол

Обобщением плоского угла на стереометрию является телесный угол — часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол).

Телесные углы измеряются в стерадианах (одна из основных единиц СИ), а также во внесистемных единицах — в частях полной сферы (то есть полного телесного угла, составляющего 4π стерадиан), в квадратных градусах, квадратных минутах и квадратных секундах.

Телесными углами являются, в частности, следующие геометрические тела:

двугранный угол — часть пространства, ограниченная двумя пересекающимися плоскостями;
трёхгранный угол — часть пространства, ограниченная тремя пересекающимися плоскостями;
многогранный угол — часть пространства, ограниченная несколькими плоскостями, пересекающимися в одной точке.

Двугранный угол может характеризоваться как линейным углом (углом между образующими его плоскостями), так и телесным углом (в качестве вершины может быть выбрана любая точка на его ребре — прямой пересечения его граней). Если линейный угол двугранного угла (в радианах) равен φ, то его телесный угол (в стерадианах) равен 2φ.

Угол между кривыми

Как в планиметрии, так и в стереометрии, а также в ряде других геометрий можно определить угол между гладкими кривыми в точке пересечения: по определению, его величина равна величине угла между касательными к кривым в точке пересечения.

Угол и скалярное произведение

Понятие угла можно определить для линейных пространств произвольной природы (и произвольной, в том числе бесконечной размерности), на которых аксиоматически введено положительно определённое скалярное произведение [math]\displaystyle{ (x,y) }[/math] между двумя элементами пространства [math]\displaystyle{ x }[/math] и [math]\displaystyle{ y. }[/math] Скалярное произведение позволяет определить также и так называемую норму (длину) элемента как квадратный корень произведения элемента на себя [math]\displaystyle{ ||x||=\sqrt{(x,x)}. }[/math] Из аксиом скалярного произведения следует неравенство Коши — Буняковского (Коши — Шварца) для скалярного произведения: [math]\displaystyle{ |(x,y)|\leqslant ||x||\cdot||y||, }[/math] откуда следует, что величина [math]\displaystyle{ \frac {(x,y)} {||x||\cdot ||y||} }[/math] принимает значения от −1 до 1, причём крайние значения достигаются тогда и только тогда, когда элементы пропорциональны (коллинеарны) друг другу (говоря геометрически — их направления совпадают или противоположны). Это позволяет интерпретировать отношение [math]\displaystyle{ \frac {(x,y)} {||x||\cdot ||y||} }[/math] как косинус угла между элементами [math]\displaystyle{ x }[/math] и [math]\displaystyle{ y. }[/math] В частности, элементы называют ортогональными, если скалярное произведение (или косинус угла) равно нулю.

В частности, можно ввести понятие угла между непрерывными на некотором интервале [math]\displaystyle{ [a,b] }[/math] функциями, если ввести стандартное скалярное произведение [math]\displaystyle{ (f,g) =\int^b_a f(x) g(x) dx, }[/math] тогда нормы функций определяются как [math]\displaystyle{ ||f||^2=\int^b_a f^2(x)dx. }[/math] Тогда косинус угла определяется стандартным образом как отношение скалярного произведения функций к их нормам. Функции также можно назвать ортогональными, если их скалярное произведение (интеграл их произведения) равно нулю.

В римановой геометрии можно аналогично определить угол между касательными векторами с помощью метрического тензора [math]\displaystyle{ g_{ij}. }[/math] Скалярное произведение касательных векторов [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] в тензорной записи будет иметь вид: [math]\displaystyle{ (u,v)=g_{ij}u^iv^j, }[/math] соответственно нормы векторов — [math]\displaystyle{ ||u||=\sqrt{|g_{ij}u^iu^j|} }[/math] и [math]\displaystyle{ ||v||=\sqrt{|g_{ij}v^iv^j|}. }[/math] Поэтому косинус угла будет определяться по стандартной формуле отношения указанного скалярного произведения к нормам векторов: [math]\displaystyle{ \cos \theta = \frac {(u,v)} {||u||\cdot ||v||} = \frac {g_{ij}u^iv^j} { \sqrt{|g_{ij}u^iu^j|\cdot |g_{ij}v^iv^j|} }. }[/math]

Угол в метрическом пространстве

Также существует ряд работ, в которых вводится понятие угла между элементами метрического пространства.

Пусть [math]\displaystyle{ (X,\rho) }[/math] — метрическое пространство. Пусть далее, [math]\displaystyle{ x,y,z }[/math] — элементы этого пространства.

К. Менгер ввёл понятие угла между вершинами [math]\displaystyle{ y }[/math] и [math]\displaystyle{ z }[/math] с вершиной в точке [math]\displaystyle{ x }[/math] как неотрицательное число [math]\displaystyle{ \widehat{yxz} }[/math], которое удовлетворяет трём аксиомам:

[math]\displaystyle{ \widehat{yxz}=\widehat{zxy} }[/math]
[math]\displaystyle{ \widehat{yxz}=0 }[/math] тогда и только тогда, когда [math]\displaystyle{ \rho(y,z)=|\rho(x,y)-\rho(x,z)| }[/math]
[math]\displaystyle{ \widehat{yxz}=\pi }[/math] тогда и только тогда, когда [math]\displaystyle{ \rho(y,z)=\rho(x,y)+\rho(x,z) }[/math]

В 1932 году Вильсон рассмотрел в качестве угла следующее выражение:

[math]\displaystyle{ \widehat{yxz}_w = \arccos \frac{\rho^2(x,y)+\rho^2(x,z)-\rho^2(y,z)}{2\rho(x,y)\rho(x,z)} }[/math]

Нетрудно видеть, что введённое выражение всегда имеет смысл и удовлетворяет трём аксиомам Менгера.

Кроме того, угол Вильсона обладает тем свойством, что в евклидовом пространстве он эквивалентен углу между элементами [math]\displaystyle{ y-x }[/math] и [math]\displaystyle{ z-x }[/math] в смысле евклидова пространства.

Измерение углов

Одним из самых распространённых инструментов для построения и измерения углов является транспортир (а также линейка — см. ниже); как правило, он используется для построения угла определённой величины. Для более или менее точного измерения углов разработано много инструментов:

угломер;
гониометр — прибор для лабораторного измерения углов;
кипрегель — геодезический угломерный инструмент.

Угловым расстоянием (или просто углом) между двумя объектами для наблюдателя называется мера угла, в вершине которого находится наблюдатель, а объекты лежат на сторонах. Для грубой оценки углов между двумя удалёнными предметами можно использовать кисть руки. На расстоянии вытянутой руки угловому расстоянию в 1 градус (1°) соответствует ширина мизинца (см. также ниже; угловая ширина среднего пальца на расстоянии вытянутой руки составляет около 2°), углу в 10 градусов — ширина сжатого кулака, расположенного горизонтально (либо поперечник ладони), углу в 20 градусов (или около 15°÷17°÷20°) — расстояние между кончиками разведённых большого и указательного пальца (пядь), а угловое расстояние от конца мизинца до конца большого пальца равно примерно четверти прямого угла. Это усреднённые данные. Рекомендуется уточнить их для своей собственной руки.

Различные методы и устройства для измерения углов характеризуются угловым разрешением, то есть минимальным углом, который может быть измерен с помощью данного метода. Наилучшим угловым разрешением обладают различные интерферометрические методы, позволяющие измерить в некоторых случаях углы в несколько микросекунд дуги (~10⁻¹¹ радиана).

Примеры практических тригонометрических измерений

Решение задач простым способом

Как измерить угол (например, на карте) с помощью сторон треугольника (например, при отсутствии инженерного/тригонометрического калькулятора (и таблиц) и отсутствии ПК (MS Office Excel) для вычисления cos) и подручными средствами — линейки с миллиметровыми делениями?
По сторонам угла отложите отрезки по 60 мм и концы соедините прямой линией. Длина этой линии в миллиметрах покажет примерно величину угла в градусах. Таким способом можно с достаточной (приемлемой) точностью измерять острые углы до 60°. Если угол больше 60°, измеряют его дополнение до 90°, 180, 270° или 360°. Для измерения дополнения до 90° или 270° из вершины угла строится с помощью треугольника перпендикуляр к одной из сторон (в равнобедренном треугольнике — медиана-биссектриса, она же является высотой).

Как измерить угол линейкой (при визуальном ориентировании на местности …и сравнить угол по карте — см. пункт 1)?
Поместите линейку с миллиметровыми делениями перед собой на расстоянии 57 см (не более 60 см) от глаза. В этом случае деление, равное 1 см, будет соответствовать углу визирования в 1°. В справедливости данного способа вы легко убедитесь, если помните, что дуга центрального угла в 1° составляет примерно 1/57 часть радиуса. Точность измерения углов с помощью линейки (также как и с помощью пальцев; см. ниже) зависит от точности положения линейки (или пальцев) на необходимом расстоянии от глаза. В этом можно быстро натренироваться с помощью нитки, длина которой соответствует расстоянию от глаза до пальцев вытянутой руки.

Как можно измерять и откладывать на местности углы без применения угломерных приборов?
Наиболее просто это можно сделать сравнением измеряемого угла с прямым. Прямой угол вы можете отложить направлениями рук, одна из которых вытянута вдоль плеч, а вторая с поднятым большим пальцем направлена так, чтобы палец правой руки был перед правым глазом (соответственно палец левой руки — перед левым глазом). Прямой угол можно глазомерно поделить на две или три равные части, каждая из которых будет соответствовать 45° или 30°.
Меньшие значения углов можно отложить или измерить на местности следующим приёмом. Прежде всего измерьте линейкой ширину трёх сомкнутых пальцев своей руки: указательного, среднего и безымянного. Если она у вас будет равна 6 см, то при вытянутой на 60 см руке угол визирования на них составит примерно 6°. Соответственно угол визирования на каждый из этих трёх пальцев будет равен в среднем 2°. Если же ширина трёх пальцев получится у вас, например, 5 см, то, чтобы углы визирования были такими же, руку надо вытягивать на 50 см.

При вытянутой руке угол визирования на большой и указательный пальцы, раздвинутые под прямым углом, составляет примерно 15°. Как это проверить и уточнить?
Прежде всего заметьте на местности ориентир и от него отложите угол 90°. Это можно сделать приёмом, описанным в предыдущей задаче. Затем от ориентира отложите шесть углов по 15° визированием на большой и указательный пальцы, раздвинутые под прямым углом. Последнее отложение угла должно составить на местности прямой угол. Если этого точно не получилось, нужно повторить отложения, держа вытянутую руку немного ближе или дальше от глаза (порядка 60 см). Этим самым вы определите расстояние, на которое нужно вытягивать руку для отложения угла 15°^[3].

Углы также можно вычислить (рассчитать) с помощью различных измерительных приборов и приспособлений — посредством тригонометрии на счётной линейке, инженерном калькуляторе (в том числе калькулятор (Windows)), с помощью функций таблицы MS Office Excel: (1) cos, (2) затем arccos, и (3) перевести, также функциями, значение радианов в градусы (°) (при наличии ПК; существуют и on-line-вычисление углов треугольника по заданным сторонам); Существуют также специальные тригонометрические таблицы: sin, cos, а также arccos, arcsin, последние, кстати, могут быть (в том числе и чаще всего) с перерасчётом в градусы.

В аналитической геометрии угол между прямыми в координатной плоскости, например, задаётся уравнением:

[math]\displaystyle{ \alpha = \mathrm{arctg}\,\left | \frac{k_1 - k_2}{1 + k_1 k_2} \right | }[/math] (см. Линейная функция; см. также #Угол и скалярное произведение)

Примечания

↑ Сидоров Л. А. Угол // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1985. — Т. 5: Слу — Я. — Стб. 467—468 — 1248 стб. : ил. — 150 000 экз.
↑ В действительности истинный период обращения Земли относительно неподвижных звёзд примерно на 4 минуты короче, чем 24 часа, см. звёздное время.
↑ Куприн А. М. На местности и по карте. — М. Недра, 1982. — 112 с.

См. также

Литература

Барабанов О. О. Начала истории прямого угла // История науки и техники. — 2015. — № 1. — С. 16—27.'
Погорелов А. В. Геометрия: учебник для 7—11 классов средней школы. — М.: Просвещение, 1992. — 383 с. — ISBN 9785090038546.
Сидоров Л. А. Угол // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1985. — Т. 5: Слу — Я. — Стб. 467‒468 — 1248 стб. : ил. — 150 000 экз.
Двугранный угол // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1979. — Т. 2: Д — Коо. — Стб. 50 — 1104 стб. : ил. — 150 000 экз.
Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 30‒31. — ISBN 5-94057-170-0.
Угломерные приборы/Угол (плоский) // Большая Советская энциклопедия (в 30 т.) / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: «Советская Энциклопедия», 1977. — Т. XXVI. — С. 459‒460. — 624 с.
Weisstein, Eric W. Line Bisector (англ.) на сайте Wolfram MathWorld.
Weisstein, Eric W. Angle (англ.) на сайте Wolfram MathWorld.
Weisstein, Eric W. Polygon (англ.) на сайте Wolfram MathWorld.
K. Menger. New Fondations of Euclidean Geometry (англ.) // THE AMERICAN JOURNAL OF MATHEMATICS 53 : журнал. — 1931. — P. 721‒745.
W. A. Wilson. On angles in certain metric spaces (англ.) // Bulletin of American Mathematical Society 39. — 1932. — P. 580‒588.

[1] Сидоров Л. А. Угол // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1985. — Т. 5: Слу — Я. — Стб. 467—468 — 1248 стб. : ил. — 150 000 экз.

[2] В действительности истинный период обращения Земли относительно неподвижных звёзд примерно на 4 минуты короче, чем 24 часа, см. звёздное время.

[3] Куприн А. М. На местности и по карте. — М. Недра, 1982. — 112 с.

[1]

[2]

[3]