Сингония

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
Триклинный родонит
Моноклинный вивианит
Ромбический фаялит
Тетрагональный анатаз
Тригональный гематит
Гексагональный берилл
Кубический спессартин

Сингони́я (от греч. σύν «согласно, вместе, рядом» + γωνία «угол»; букв. «сходноугольность») — классификация кристаллографических групп симметрии, кристаллов и кристаллических решёток в зависимости от системы координат (координатного репера); группы симметрии с единой координатной системой объединяются в одну сингонию. Кристаллы, принадлежащие к одной и той же сингонии, имеют подобные углы и рёбра элементарных ячеек.

Кристалли́ческая систе́ма — классификация кристаллов и кристаллографических групп, основанная на наборе элементов симметрии, описывающих кристалл и принадлежащих кристаллографической группе.

Систе́ма решётки — классификация кристаллических решёток в зависимости от их симметрии.

В литературе существует путаница всех трёх понятий: сингонии[1], кристаллической системы[2] и системы решётки[3], — которые часто используются как синонимы.

В русскоязычной литературе термин «система решётки» пока не используется. Обычно авторы смешивают это понятие с кристаллической системой. В книге «Основы кристаллографии»[4] авторы используют термин «Сингония решётки» («По симметрии узлов пространственные решетки могут быть разделены на семь категорий, называемых сингониями решеток»). У тех же авторов сингонии называются системами («Наиболее установившейся классификацией групп является их разделение на шесть систем по признаку симметрии комплексов граней»).

Сингония

Исторически первой классификацией кристаллов было деление на сингонии, в зависимости от кристаллографической системы координат. За координатные оси выбирались оси симметрии кристалла, а при их отсутствии — ребра кристалла. В свете современного знания о структуре кристаллов таким направлениям соответствуют трансляции кристаллической решётки, и за систему координат выбираются трансляции ячейки Браве в стандартной установке. В зависимости от соотношения между длинами этих трансляций и углами между ними [math]\displaystyle{ \alpha, \beta, \gamma }[/math] выделяют шесть различных сингоний, которые распадаются на три категории в зависимости от числа равных длин трансляций[5]:

  • Низшая категория (все трансляции не равны друг другу)
    • Триклинная: [math]\displaystyle{ a\ne b \ne c }[/math], [math]\displaystyle{ \alpha \ne \beta \ne \gamma \ne 90 ^\circ }[/math]
    • Моноклинная: [math]\displaystyle{ a\ne b \ne c }[/math], [math]\displaystyle{ \alpha = \gamma = 90^\circ, \beta\ne90^\circ }[/math]
    • Ромбическая: [math]\displaystyle{ a\ne b \ne c }[/math], [math]\displaystyle{ \alpha = \beta = \gamma = 90^\circ }[/math]
  • Средняя категория (две трансляции из трёх равны между собой)
    • Тетрагональная: [math]\displaystyle{ a=b \ne c }[/math], [math]\displaystyle{ \alpha = \beta = \gamma = 90^\circ }[/math]
    • Гексагональная: [math]\displaystyle{ a=b \ne c }[/math], [math]\displaystyle{ \alpha = \beta =90^\circ, \gamma = 120^\circ }[/math]
  • Высшая категория (все трансляции равны между собой)
    • Кубическая: [math]\displaystyle{ a=b=c }[/math], [math]\displaystyle{ \alpha = \beta = \gamma = 90^\circ }[/math]

Кристаллическая система

Разбиение на кристаллические системы выполняется в зависимости от набора элементов симметрии, описывающих кристалл. Такое деление приводит к семи кристаллическим системам, две из которых — тригональная (с одной осью 3-го порядка) и гексагональная (с одной осью 6-го порядка) — имеют одинаковую по форме элементарную ячейку и поэтому относятся к одной, гексагональной, сингонии. Иногда говорят, что гексагональная сингония подразделяется на две подсингонии[6] или гипосингонии.[7]

Кристаллические системы также разбиваются на три категории, в зависимости от числа осей высшего порядка (осей выше второго порядка).

Возможные в трехмерном пространстве кристаллические системы с определяющими их элементами симметрии, то есть элементами симметрии, наличие которых необходимо для отнесения кристалла или точечной группы к определенной кристаллической системе:

  • Низшая категория (нет осей высшего порядка)
    • Триклинная: нет симметрии или только центр инверсии [math]\displaystyle{ \overline{1} }[/math]
    • Моноклинная: одна ось [math]\displaystyle{ 2 }[/math]-го порядка и/или плоскость симметрии [math]\displaystyle{ m }[/math]
    • Ромбическая: три взаимно-перпендикулярных оси [math]\displaystyle{ 2 }[/math]-го порядка и/или плоскости симметрии [math]\displaystyle{ m }[/math] (направлением плоскости симметрии считается перпендикуляр к ней)
  • Средняя категория (одна ось высшего порядка)
  • Высшая категория (несколько осей высшего порядка)

Кристаллическая система пространственной группы определяется системой соответствующей ей точечной группы. Например, группы Pbca, Cmcm, Immm, Fddd (класс mmm) принадлежат к ромбической системе.

Современное определение кристаллической системы (применимое не только к обычным трёхмерным группам, но и для пространств любых размерностей) относит точечные группы (и производные от них пространственные группы) к одной кристаллической системе, если эти группы могут комбинироваться с одними и теми же типами решёток Браве. Например, группы mm2 и 222 обе принадлежат ромбической системе, так как для каждой из них существуют пространственные группы со всеми типами ромбической решётки (Pmm2, Cmm2, Imm2, Fmm2 и P222, C222, I222, F222), в то же время группы 32 и 6 не принадлежат одной кристаллической системе, так как для группы 32 допустимы примитивная и дважды-центрированная гексагональные ячейки (группы P321 и R32), а группа 6 комбинируется только с примитивной гексагональной ячейкой (есть группа P6, но не существует R6).

Система решётки (Lattice system)

Описывает типы кристаллических решёток. Вкратце: решётки относятся к одному типу, если их точечные группы симметрии (при рассмотрении решёток как геометрических объектов) одинаковы. Такие точечные группы, описывающие симметрию решётки, называются голоэдрией.[8]

Всего существует семь систем решёток, которые, аналогично предыдущим классификациям (сингония и кристаллическая система) делятся на три категории.

  • Низшая категория (все трансляции не равны друг другу)
    • Триклинная: [math]\displaystyle{ a\ne b \ne c }[/math], [math]\displaystyle{ \alpha \ne \beta \ne \gamma \ne 90 ^\circ }[/math]
    • Моноклинная: [math]\displaystyle{ a\ne b \ne c }[/math], [math]\displaystyle{ \alpha = \gamma = 90^\circ, \beta\ne90^\circ }[/math]
    • Ромбическая: [math]\displaystyle{ a\ne b \ne c }[/math], [math]\displaystyle{ \alpha = \beta = \gamma = 90^\circ }[/math]
  • Средняя категория
    • Тетрагональная: [math]\displaystyle{ a=b \ne c }[/math], [math]\displaystyle{ \alpha = \beta = \gamma = 90^\circ }[/math]
    • Гексагональная: [math]\displaystyle{ a=b \ne c }[/math], [math]\displaystyle{ \alpha = \beta =90^\circ, \gamma = 120^\circ }[/math]
    • Ромбоэдрическая: [math]\displaystyle{ a = b = c }[/math], [math]\displaystyle{ \alpha = \beta = \gamma \lt 120^\circ \ne 90^\circ }[/math]
  • Высшая категория (все трансляции равны между собой)
    • Кубическая: [math]\displaystyle{ a=b=c }[/math], [math]\displaystyle{ \alpha = \beta = \gamma = 90^\circ }[/math]

Не следует путать ромбоэдрическую систему решётки с тригональной кристаллической системой. Кристаллы ромбоэдрической системы решётки всегда принадлежат тригональной кристаллической системе, но тригональные кристаллы могут принадлежать как ромбоэдрической, так и гексагональной системам решётки. Например, группы R3 и P321 (обе из тригональной кристаллической системы) принадлежат к разным системам решётки (ромбоэдрической и гексагональной, соответственно).

Общее определение, применимое для пространств любых размерностей — Решётки относятся к одному типу, если они комбинируются с одними и теми же точечными группами. Например, все ромбические решётки (ромбическая P, ромбическая C, ромбическая I и ромбическая F) относятся к одному типу, так как они комбинируются с точечными группами 222, mm2 и mmm, образуя пространственные группы P222, Pmm2, Pmmm; C222, Cmm2, Cmmm; I222, Imm2, Immm; F222, Fmm2, Fmmm. В то же время ячейки гексагональной сингонии (примитивная P и дважды центрированная R) соответствуют разным системам решётки: обе комбинируются с точечными группами тригональной кристаллической системы, но с группами гексагональной системы комбинируется только примитивная ячейка (существуют группы P6, P6, P6/m, P622, P6mm, P6m2, P6/mmm, но не существует групп R6, R6, R6/m, R622, R6mm, R6m2, R6/mmm).

Связь между сингонией, кристаллической системой и системой решётки в трёхмерном пространстве дана в следующей таблице:

Сингония Кристаллическая система Точечные группы Число пространственных групп Решётка Браве[9] Система решётки Голоэдрия
Триклинная 1, 1 2 aP Триклинная 1
Моноклинная 2, m, 2/m 13 mP, mS Моноклинная 2/m
Ромбическая 222, mm2, mmm 59 oP, oS, oI, oF Ромбическая mmm
Тетрагональная 4, 4, 422, 4mm, 42m, 4/m, 4/mmm 68 tP, tI Тетрагональная 4/mmm
Гексагональная Тригональная 3, 3, 32, 3m, 3m 7 hR Ромбоэдрическая 3m
18 hP Гексагональная 6/mmm
Гексагональная 6, 6, 622, 6mm, 6m2, 6/m, 6/mmm 27
Кубическая 23, m3, 43m, 432, m3m 36 cP, cI, cF Кубическая m3m
Всего: 6 7 32 230 14 7

Обзор точечных групп

Основной источник: [10][11][12]
Кристаллическая система точечная группа / класс симметрии Символ Шёнфлиса Международный символ Символ Шубникова Тип
триклинная моноэдрический C1 [math]\displaystyle{ 1\ }[/math] [math]\displaystyle{ 1\ }[/math] энантиоморфный полярный
пинакоидальный Ci [math]\displaystyle{ \bar{1} }[/math] [math]\displaystyle{ \tilde{2} }[/math] центросимметричный
моноклинная диэдрический осевой C2 [math]\displaystyle{ 2\ }[/math] [math]\displaystyle{ 2\ }[/math] энантиоморфный полярный
диэдрический безосный (доматический) Cs [math]\displaystyle{ m\ }[/math] [math]\displaystyle{ m\ }[/math] полярный
призматический C2h [math]\displaystyle{ 2/m\ }[/math] [math]\displaystyle{ 2:m\ }[/math] центросимметричный
Ромбическая ромбо-тетраэдрический D2 [math]\displaystyle{ 222\ }[/math] [math]\displaystyle{ 2:2\ }[/math] энантиоморфный
ромбо-пирамидальный C2v [math]\displaystyle{ mm2\ }[/math] [math]\displaystyle{ 2 \cdot m\ }[/math] полярный
ромбо-дипирамидальный D2h [math]\displaystyle{ mmm\ }[/math] [math]\displaystyle{ m \cdot 2:m\ }[/math] центросимметричный
Тетрагональная тетрагонально-пирамидальный C4 [math]\displaystyle{ 4\ }[/math] [math]\displaystyle{ 4\ }[/math] энантиоморфный полярный
тетрагонально-тетраэдрический S4 [math]\displaystyle{ \bar{4} }[/math] [math]\displaystyle{ \tilde{4} }[/math]
тетрагонально-дипирамидальный C4h [math]\displaystyle{ 4/m\ }[/math] [math]\displaystyle{ 4:m\ }[/math] центросимметричный
тетрагонально-трапецоэдрический D4 [math]\displaystyle{ 422\ }[/math] [math]\displaystyle{ 4:2\ }[/math] энантиоморфный
дитетрагонально-пирамидальный C4v [math]\displaystyle{ 4mm\ }[/math] [math]\displaystyle{ 4 \cdot m\ }[/math] полярный
тетрагонально-скаленоэдрический D2d [math]\displaystyle{ \bar{4}2m\ }[/math] или [math]\displaystyle{ \bar{4}m2 }[/math] [math]\displaystyle{ \tilde{4}\cdot m }[/math]
дитетрагонально-дипирамидальный D4h [math]\displaystyle{ 4/mmm\ }[/math] [math]\displaystyle{ m \cdot 4:m\ }[/math] центросимметричный
Тригональная тригонально-пирамидальный C3 [math]\displaystyle{ 3 }[/math] [math]\displaystyle{ 3\ }[/math] энантиоморфный полярный
ромбоэдрический S6 (C3i) [math]\displaystyle{ \bar{3} }[/math] [math]\displaystyle{ \tilde{6} }[/math] центросимметричный
тригонально-трапецоэдрический D3 [math]\displaystyle{ 32\ }[/math] или [math]\displaystyle{ 321\ }[/math] или [math]\displaystyle{ 312\ }[/math] [math]\displaystyle{ 3:2\ }[/math] энантиоморфный
дитригонально-пирамидальный C3v [math]\displaystyle{ 3m\ }[/math] или [math]\displaystyle{ 3m1\ }[/math] или [math]\displaystyle{ 31m\ }[/math] [math]\displaystyle{ 3 \cdot m\ }[/math] полярный
дитригонально-скаленоэдрический D3d [math]\displaystyle{ \bar{3} m\ }[/math] или [math]\displaystyle{ \bar{3} m 1 }[/math] или [math]\displaystyle{ \bar{3} 1 m }[/math] [math]\displaystyle{ \tilde{6}\cdot m }[/math] центросимметричный
Гексагональная гексагонально-пирамидальный C6 [math]\displaystyle{ 6\ }[/math] [math]\displaystyle{ 6\ }[/math] энантиоморфный полярный
тригонально-дипирамидальный C3h [math]\displaystyle{ \bar{6} }[/math] [math]\displaystyle{ 3:m\ }[/math]
гексагонально-дипирамидальный C6h [math]\displaystyle{ 6/m\ }[/math] [math]\displaystyle{ 6:m\ }[/math] центросимметричный
гексагонально-трапецоэдрический D6 [math]\displaystyle{ 622\ }[/math] [math]\displaystyle{ 6:2\ }[/math] энантиоморфный
дигексагонально-пирамидальный C6v [math]\displaystyle{ 6mm\ }[/math] [math]\displaystyle{ 6 \cdot m\ }[/math] полярный
дитригонально-дипирамидальный D3h [math]\displaystyle{ \bar{6}m2 }[/math] или [math]\displaystyle{ \bar{6}2m }[/math] [math]\displaystyle{ m \cdot 3:m\ }[/math]
дигексагонально-дипирамидальный D6h [math]\displaystyle{ 6/mmm\ }[/math] [math]\displaystyle{ m \cdot 6:m\ }[/math] центросимметричный
Кубическая тритетраэдрический T [math]\displaystyle{ 23\ }[/math] [math]\displaystyle{ 3/2\ }[/math] энантиоморфный
дидодекаэдрический Th [math]\displaystyle{ m\bar{3}\ }[/math] [math]\displaystyle{ \tilde{6}/2 }[/math] центросимметричный
гексатетраэдрический Td [math]\displaystyle{ \bar{4}3m }[/math] [math]\displaystyle{ 3/\tilde{4} }[/math]
триоктаэдрический O [math]\displaystyle{ 432\ }[/math] [math]\displaystyle{ 3/4\ }[/math] энантиоморфный
гексоктаэдрический Oh [math]\displaystyle{ m\bar{3}m }[/math] [math]\displaystyle{ \tilde{6}/4 }[/math] центросимметричный

Классификация решеток

Сингония Тип центрировки ячейки Браве
примитивная базо-
центрированная		 объёмно-
центрированная		 гране-
центрированная		 дважды
объёмно-
центрированная
Триклинная
(параллелепипед) 		Triclinic
Моноклинная
(призма с параллелограммом в основании) 		Monoclinic, simple Monoclinic, centered
Ромбическая
(прямоугольный параллелепипед) 		Orthohombic, simple Orthohombic, base-centered Orthohombic, body-centered Orthohombic, face-centered
Тетрагональная
(прямоугольный параллелепипед с квадратом в основании) 		Tetragonal, simple Tetragonal, body-centered
Гексагональная
(призма с основанием правильного центрированного шестиугольника) 		Hexagonal Hexagonal
Тригональная
(равносторонний параллелепипед —ромбоэдр) 		Rhombohedral
Кубическая
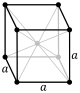
(куб) 		Cubic, simple Cubic, body-centered Cubic, face-centered

История

Первая геометрическая классификация кристаллов была дана независимо Христианом Вейсом и Фридрихом Моосом в начале 19 века. Оба учёных классифицировали кристаллы по симметрии их внешней формы (огранки). При этом Вейс фактически вводит понятие кристаллографической оси (оси симметрии). По Вейсу «Ось есть линия, господствующая над всей фигурой кристалла, так как вокруг неё все части расположены подобным образом и относительно неё они соответствуют друг другу взаимно»[13]. В своей работе «Наглядное представление об естественных делениях систем кристаллизации» Вейс классифицировал кристаллы по наличию осей на четыре больших раздела кристаллических форм, «систем кристаллизации», соответствующих современному понятию сингонии[14]. В скобках даны современные названия.

  • 1 раздел — «правильная», «сфероэдрическая», «равноосная», «равночленная» (кубическая) система: три измерения одинаковы, образуя между собой прямые углы.
    • подраздел гомосфероэдрическая система (кристаллы симметрии m3m)
    • подраздел гемисфероэдрическая система (кристаллы симметрии 432, 43m и m3)
  • 2 раздел — «четырёхчленная» (тетрагональная) система: оси образуют между собой прямые углы, две оси равны между собой и не равны третьей.
  • 3 раздел — «двучленная» система: все три оси неравны и образуют между собой прямые углы.
    • подраздел «дву-и-двучленная» (ромбическая) система
    • подраздел «дву-и-одночленная» (моноклинная) система
    • подраздел «одно-и-одночленная» (триклинная) система
  • 4 раздел — одна неравная ось перпендикулярна трём равным осям, образующим между собой углы в 120°.
    • подраздел «шестичленная» (гексагональная) система:
    • подраздел «три-и-тричленная» или «ромбоэдрическая» (тригональная) система:

Для моноклинной и триклинной сингонии Вейс использовал прямоугольную систему координат (современные кристаллографические координатные системы для этих сингоний являются косоугольными).

Примерно в то же время Фридрих Моос развил концепцию кристаллических систем[15]. Каждая система характеризуется простейшей, «основной формой», граней, из которой можно вывести все остальные формы данной системы. Таким образом Моос получил следующие четыре системы:

  • 1. Ромбоэдрическая система (гексагональная сингония). Основная форма — ромбоэдр.
  • 2. Пирамидальная система (тетрагональная сингония). Основная форма — тетрагональная бипирамида.
  • 3. Тессулярная система (кубическая сингония). Основные формы — куб и октаэдр.
  • 4. Призматическая система (ромбическая сингония). Основная форма — ромбическая бипирамида.
    • Гемипризматическая подсистема (моноклинная сингония)
    • Тетартопризматическая подсистема (триклинная сингония)

В обоих классификациях Вейс и Моос выделяет всего четыре системы, хотя перечислены все шесть сингоний, только моноклинную и триклинную сингонии они рассматривают как подсистемы ромбической. Согласно его собственному утверждению, Моос развил эту концепцию в 1812-14 годах, что и послужило предметом спора с Вейсом о приоритете открытия кристаллических систем. В отличие от Вейса, Моос указал на необходимость косоугольной системы осей для моноклинных и триклинных кристаллов.

Окончательно развил и ввёл в кристаллографию косоуголные системы его ученик Карл Фридрих Науман. Науман положил в основу классификации кристаллографические оси и углы между ними, таким образом впервые выделив все шесть сингоний[16][17]. Интересно, что уже в 1830 году Науман использует названия сингоний, которые идентичны или близки современным (названия тетрагональная, гексагональная и ромбическая были изначально предложены Брейтгауптом).

  • 1. Тессеральная (от tessera — куб) — все три угла между координатными осями прямые, все три оси равны.
  • 2. Тетрагональная — все три угла прямые, две оси равны.
  • 3. Гексагональная — единственная четырёхосевая система: одна неравная ось перпендикулярна трём равным осям, образующим между собой углы в 60°.
  • 4. Ромбическая — все три угла прямые, все оси неравны.
  • 5. Моноклиноэдрическая — два прямых угла и один косой.
  • 6. Диклиноэдрическая — два косых угла и один прямой.
  • 7. Триклиноэдрическая — все три угла косые.

Поскольку в то время теория симметрии только развивалась, в списке систем появилась необычная диклиноэдрическая (диклинная) система. Такая кристаллическая система в принципе невозможна в трёхмерном пространстве, так как наличие оси симметрии всегда гарантирует наличие перпендикулярных к оси трансляций, выбираемых за координатные оси. Диклинная система просуществовала в кристаллографии примерно полвека (хотя уже в 1856 году Дюфренуа показал, что это лишь частный случай триклинной системы). В 1880 году Дана в своей знаменитой книге «Система минералогии»[18] упоминает «так называемую диклинную систему», но при этом отмечает, что не известно ни одного природного или искусственного кристалла, принадлежащего данной системе, и что более того, математически доказано, что существует всего шесть кристаллических систем. Сам Науман до конца жизни верил в диклинную сингонию, и в девятом издании «Оснований минералогии»[19], вышедшем в 1874 году посмертно, эта сингония по-прежнему присутствует в списке, хотя Науман и замечает, что эта система встречается только в нескольких искусственных солях, и далее не рассматривает её.

Названия кристаллографических сингоний у авторов XIX века

Автор Кубическая Тетрагональная Гексагональная Ромбическая Моноклинная Триклинная
Вейс Правильная, Сферическая, Шаровая, Сферономическая, Равноосная, Равночленная Четырёхчленная, Дву‑и‑одноосная Шестичленная, Три‑и‑одноосная Дву‑и‑двучленная, Одно‑и‑одноосная Дву‑и‑одночленная Одно‑и‑одночленная
Моос Тессулярная, Тесселярная Пирамидальная Ромбоэдрическая Призматическая, Ортотипная Гемипризматическая, Гемиортотипная Тетартопризматическая, Анортотипная
Брейтгаупт Тетрагональная Гексагональная Ромбическая Гемиромбическая Тетарторомбическая
Науман Тессеральная Тетрагональная Гексагональная Ромбическая, Анизометрическая Моноклиноэдрическая, Клиноромбическая Триклиноэдрическая, Триклинометрическая
Гаусман Изометрическая Монодиметрическая Монотриметрическая Триметрическая, Орторомбическая Клиноромбическая, Орторомбоидическая Клиноромбоидическая
Миллер 1839 Октаэдрическая Пирамидальная Ромбоэдрическая Призматическая Наклонно-призматическая Дважды-наклонно-призматическая
Гадолин Правильная Квадратная Гексагональная Ромбическая Моноклиноэдрическая Триклиноэдрическая
Другие авторы Тетраэдрическая (Бёдан), Кубическая (Дюфренуа) Диметрическая Двучленная (Квенштедт) Моноклинометрическая (Франкенгейм),
Авгитовая (Гайдингер)		 Триклиническая (Франкенгейм),
Анортическая (Гайдингер)

Впервые деление на семь кристаллографических систем дано в 1850 году в работе Огюста Браве «Мемуар о системах точек, правильно распределённых на плоскости или в пространстве»[20]. Фактически это первое деление, основанное на элементах симметрии, а не на системах координат. Поэтому все предыдущие классификации соответствуют сегодняшнему определению сингонии, в то время как классификация Браве — это классификация по кристаллическим системам (строго говоря, системам решётки).

Браве делит решётки в зависимости от их симметрии на 7 систем (классы совокупностей).

  • 1. Тричетверные (кубическая система)
  • 2. Шестерные (гексагональная система)
  • 3. Четверные (тетрагональная система)
  • 4. Тройные (ромбоэдрическая система)
  • 5. Тридвойные (ромбическая система)
  • 6. Двойные (моноклинная система)
  • 7. Асимметричные (триклинная система)

При этом сам Браве отмечает, что ещё Гаюи делил решётки гексагональной системы (по классификации Наумана) «на кристаллы, порожденные правильной гексагональной призмой, и кристаллы, порожденные ядром в виде ромбоэдра».

Классификация групп в многомерных пространствах

Во второй половине XX века были изучены и классифицированы кристаллографические группы в четырёхмерном, пятимерном и шестимерном пространствах. С увеличением размерности число групп и классов значительно возрастает[21]. В скобках указано число энантиоморфных пар.

Размерность пространства: 1 2 3 4 5 6
Число сингоний 1 4 6 23 (+6) 32 91
Число систем решёток 1 4 7 33 (+7) 57 220
Число кристаллических систем 1 4 7 33 (+7) 59 251
Число решёток Браве 1 5 14 64 (+10) 189 841
Число точечных групп 2 10 32 227 (+44) 955 7103
Число пространственных групп 2 17 219 (+11) 4783 (+111) 222018 (+79) 28927915 (+?)[22]

В четырёхмерном пространстве элементарная ячейка определяется четырьмя сторонами ([math]\displaystyle{ a, b, c, d }[/math]) и шестью углами между ними ([math]\displaystyle{ \alpha, \beta, \gamma, \delta, \epsilon, \zeta }[/math]). Следующие соотношения между ними определяют 23 сингонии:

  1. Гексаклинная: [math]\displaystyle{ a\ne b \ne c \ne d, \alpha \ne \beta \ne \gamma \ne \delta \ne \epsilon \ne \zeta \ne 90 ^\circ }[/math]
  2. Триклинная: [math]\displaystyle{ a\ne b \ne c \ne d, \alpha \ne \beta \ne \gamma \ne 90 ^\circ, \delta = \epsilon = \zeta = 90 ^\circ }[/math]
  3. Диклинная: [math]\displaystyle{ a\ne b \ne c \ne d, \alpha \ne 90 ^\circ, \beta = \gamma = \delta = \epsilon = 90 ^\circ, \zeta \ne 90 ^\circ }[/math]
  4. Моноклинная: [math]\displaystyle{ a\ne b \ne c \ne d, \alpha \ne 90 ^\circ, \beta = \gamma = \delta = \epsilon = \zeta = 90 ^\circ }[/math]
  5. Ортогональная: [math]\displaystyle{ a\ne b \ne c \ne d, \alpha = \beta = \gamma = \delta = \epsilon = \zeta = 90 ^\circ }[/math]
  6. Тетрагональная моноклинная: [math]\displaystyle{ a\ne b = c \ne d, \alpha \ne 90 ^\circ, \beta = \gamma = \delta = \epsilon = \zeta = 90 ^\circ }[/math]
  7. Гексагональная моноклинная: [math]\displaystyle{ a\ne b = c \ne d, \alpha \ne 90 ^\circ, \beta = \gamma = \delta = \epsilon = 90 ^\circ, \zeta = 120 ^\circ }[/math]
  8. Дитетрагональная диклинная: [math]\displaystyle{ a = d \ne b = c, \alpha = \zeta = 90 ^\circ, \beta = \epsilon \ne 90 ^\circ, \gamma \ne 90 ^\circ, \delta = 180 ^\circ - \gamma }[/math]
  9. Дитригональная диклинная: [math]\displaystyle{ a = d \ne b = c, \alpha = \zeta = 120 ^\circ, \beta = \epsilon \ne 90 ^\circ, \gamma \ne \delta \ne 90 ^\circ, \cos \delta = \cos \beta - \cos \gamma }[/math]
  10. Тетрагональная ортогональная: [math]\displaystyle{ a\ne b = c \ne d, \alpha = \beta = \gamma = \delta = \epsilon = \zeta = 90 ^\circ }[/math]
  11. Гексагональная ортогональная: [math]\displaystyle{ a\ne b = c \ne d, \alpha = \beta = \gamma = \delta = \epsilon = 90 ^\circ, \zeta = 120 ^\circ }[/math]
  12. Дитетрагональная моноклинная: [math]\displaystyle{ a = d \ne b = c, \alpha = \gamma = \delta = \zeta = 90 ^\circ, \beta = \epsilon \ne 90 ^\circ }[/math]
  13. Дитригональная моноклинная: [math]\displaystyle{ a = d \ne b = c, \alpha = \zeta = 120 ^\circ, \beta = \epsilon \ne 90 ^\circ, \gamma = \delta \ne 90 ^\circ, \cos \gamma = -\color{Black}\tfrac{1}{2} \cos \beta }[/math]
  14. Дитетрагональная ортогональная: [math]\displaystyle{ a = d \ne b = c, \alpha = \beta = \gamma = \delta = \epsilon = \zeta = 90 ^\circ }[/math]
  15. Гексагональная тетрагональная: [math]\displaystyle{ a = d \ne b = c, \alpha = \beta = \gamma = \delta = \epsilon = 90 ^\circ, \zeta = 120 ^\circ }[/math]
  16. Дигексагональная ортогональная: [math]\displaystyle{ a = d \ne b = c, \alpha = \zeta = 120 ^\circ, \beta = \gamma = \delta = \epsilon = 90 ^\circ }[/math]
  17. Кубическая ортогональная: [math]\displaystyle{ a = b = c \ne d, \alpha = \beta = \gamma = \delta = \epsilon = \zeta = 90 ^\circ }[/math]
  18. Октагональная: [math]\displaystyle{ a = b = c = d, \alpha = \gamma = \zeta \ne 90 ^\circ, \beta = \epsilon = 90 ^\circ, \delta = 180 ^\circ - \alpha }[/math]
  19. Декагональная: [math]\displaystyle{ a = b = c = d, \alpha = \gamma = \zeta \ne \beta = \delta = \epsilon, \cos \beta = -0.5 - \cos \alpha }[/math]
  20. Додекагональная: [math]\displaystyle{ a = b = c = d, \alpha = \zeta = 90 ^\circ, \beta = \epsilon = 120 ^\circ, \gamma = \delta \ne 90 ^\circ }[/math]
  21. Ди-изогексагональная ортогональная: [math]\displaystyle{ a = b = c = d, \alpha = \zeta = 120 ^\circ, \beta = \gamma = \delta = \epsilon = 90 ^\circ }[/math]
  22. Икосагональная: [math]\displaystyle{ a = b = c = d, \alpha = \beta = \gamma = \delta = \epsilon = \zeta, \cos \alpha = -\color{Black}\tfrac{1}{4} }[/math]
  23. Гиперкубическая: [math]\displaystyle{ a = b = c = d, \alpha = \beta = \gamma = \delta = \epsilon = \zeta = 90 ^\circ }[/math]

Связь между сингонией, кристаллической системой и системой решётки в четырёхмерном пространстве дана в следующей таблице[23][24]. Звёздочками отмечены энантиоморфные системы. В скобках указано число энантиоморфных групп (или решёток).

Номер
сингонии 		Сингония Кристаллическая система Номер
системы 		Число точечных групп Число пространственных групп Число решёток Браве Система решётки
I Гексаклинная 1 2 2 1 Гексаклинная P
II Триклинная 2 3 13 2 Триклинная P, S
III Диклинная 3 2 12 3 Диклинная P, S, D
IV Моноклинная 4 4 207 6 Моноклинная P, S, S, I, D, F
V Ортогональная Безосная ортогональная 5 2 2 1 Ортогональная KU
112 8 Ортогональная P, S, I, Z, D, F, G, U
Осевая ортогональная 6 3 887
VI Тетрагональная моноклинная 7 7 88 2 Тетрагональная моноклинная P, I
VII Гексагональная моноклинная Тригональная моноклинная 8 5 9 1 Гексагональная моноклинная R
15 1 Гексагональная моноклинная P
Гексагональная моноклинная 9 7 25
VIII Дитетрагональная диклинная* 10 1 (+1) 1 (+1) 1 (+1) Дитетрагональная диклинная P*
IX Дитригональная диклинная* 11 2 (+2) 2 (+2) 1 (+1) Дитригональная диклинная P*
X Тетрагональная ортогональная Инверсионная тетрагональная ортогональная 12 5 7 1 Тетрагональная ортогональная KG
351 5 Тетрагональная ортогональная P, S, I, Z, G
Поворотная тетрагональная ортогональная 13 10 1312
XI Гексагональная ортогональная Тригональная ортогональная 14 10 81 2 Гексагональная ортогональная R, RS
150 2 Гексагональная ортогональная P, S
Гексагональная ортогональная 15 12 240
XII Дитетрагональная моноклинная* 16 1 (+1) 6 (+6) 3 (+3) Дитетрагональная моноклинная P*, S*, D*
XIII Дитригональная моноклинная* 17 2 (+2) 5 (+5) 2 (+2) Дитригональная моноклинная P*, RR*
XIV Дитетрагональная ортогональная Крипто-дитетрагональная ортогональная 18 5 10 1 Дитетрагональная ортогональная D
165 (+2) 2 Дитетрагональная ортогональная P, Z
Дитетрагональная ортогональная 19 6 127
XV Гексагональная тетрагональная 20 22 108 1 Гексагональная тетрагональная P
XVI Дигексагональная ортогональная Крипто-дитригональная ортогональная* 21 4 (+4) 5 (+5) 1 (+1) Дигексагональная ортогональная G*
5 (+5) 1 Дигексагональная ортогональная P
Дигексагональная ортогональная 23 11 20
Дитригональная ортогональная 22 11 41
16 1 Дигексагональная ортогональная RR
XVII Кубическая ортогональная Простая кубическая ортогональная 24 5 9 1 Кубическая ортогональная KU
96 5 Кубическая ортогональная P, I, Z, F, U
Сложная кубическая ортогональная 25 11 366
XVIII Октагональная* 26 2 (+2) 3 (+3) 1 (+1) Октагональная P*
XIX Декагональная 27 4 5 1 Декагональная P
XX Додекагональная* 28 2 (+2) 2 (+2) 1 (+1) Додекагональная P*
XXI Ди-изогексагональная ортогональная Простая ди-изогексагональная ортогональная 29 9 (+2) 19 (+5) 1 Ди-изогексагональная ортогональная RR
19 (+3) 1 Ди-изогексагональная ортогональная P
Сложная ди-изогексагональная ортогональная 30 13 (+8) 15 (+9)
XXII Икосагональная 31 7 20 2 Икосагональная P, SN
XXIII Гиперкубическая Октагональная гиперкубическая 32 21 (+8) 73 (+15) 1 Гиперкубическая P
107 (+28) 1 Гиперкубическая Z
Додекагональная гиперкубическая 33 16 (+12) 25 (+20)
Всего: 23 (+6) 33 (+7) 227 (+44) 4783 (+111) 64 (+10) 33 (+7)

См. также

Примечания

  1. ↑ Crystal family - Online Dictionary of Crystallography. Дата обращения: 22 февраля 2009. Архивировано 21 марта 2013 года.
  2. ↑ Crystal system - Online Dictionary of Crystallography. Дата обращения: 22 февраля 2009. Архивировано 21 марта 2013 года.
  3. ↑ Lattice system - Online Dictionary of Crystallography. Дата обращения: 29 апреля 2013. Архивировано 29 апреля 2013 года.
  4. ↑ Шубников А. В., Бокий Г. Б., Флинт Е. Е., Основы кристаллографии, Изд-во АН СССР, 1940
  5. ↑ Загальская Ю.Г., Литвинская Г.П., Егоров-Тисменко Ю.К. Геометрическая кристаллография. — М.: Издательство Московского университета, 1986. — 168 с.
  6. ↑ "Ю. К. Егоров-Тисменко, Г. П. Литвинская, Теория симметрии кристаллов, ГЕОС, 2000. Глава III. Координатные системы, категории, сингонии.". Дата обращения: 12 января 2021. Архивировано 13 января 2021 года.
  7. ↑ Фёдоров Е. С., Курс кристаллографии. Изд. 3-е, 1901 online
  8. ↑ Holohedry - Online Dictionary of Crystallography. Дата обращения: 30 января 2013. Архивировано 21 марта 2013 года.
  9. ↑ de Wolff et al., Nomenclature for crystal families, Bravais-lattice types and arithmetic classes, Acta Cryst. (1985). A41, 278—280. online Архивная копия от 27 января 2013 на Wayback Machine
  10. ↑ Вайнштейн Б.К. Современная кристаллография. Том 1. Симметрия кристаллов, методы структурной кристаллографии. Наука, Москва, 1979.
  11. ↑ Сиротин Ю.И., Шаскольская М.П. Основы кристаллофизики. Наука, Москва, 1979.
  12. ↑ Флинт Е.Е. Практическое руководство по геометрической кристаллографии. Изд-е 3-е, перараб. и доп., Госгеолтехиздат, Москва, 1956.
  13. ↑ C. S. Weiss De indagando formarum crystallinarum charactere geometrico principali dissertatio. Lipsiae [Leipzig] 1809
  14. ↑ C. S. Weiss: Ueber die natürlichen Abtheilungen der Crystallisations Systeme. Abhandl. k. Akad. Wiss., Berlin 1814—1815, S. 290—336.
  15. ↑ Friedrich Mohs: Grund-Riß der Mineralogie. Erster Theil. Terminologie, Systematik, Nomenklatur, Charakteristik. Dresden 1822
  16. ↑ Carl Friedrich Naumann, Lehrbuch der Mineralogie Mineralogie, 1828 online
  17. ↑ Carl Friedrich Naumann, Lehrbuch der reinen und angewandten Krystallographie, 1830 online
  18. ↑ Edward Salisbury Dana, James Dwight Dana, A text-book of mineralogy, 1880 online
  19. ↑ Carl Friedrich Naumann, Elemente der mineralogie, 1874 online
  20. ↑ Bravais, A. (1850) Mémoire sur les systèmes formés par les points distribués régulièrement sur un plan ou dans l’espace. Journal de L’Ecole Polytechnique.
  21. ↑ B. Souvignier: «Enantiomorphism of crystallographic groups in higher dimensions with results in dimensions up to 6». Acta Crystallographica Section A, vol.59, pp.210-220, 2003.
  22. ↑ The CARAT Homepage. Дата обращения: 5 мая 2015. Архивировано 5 марта 2016 года. Часть вычислений в работе Souvignier (2003) для шестимерного пространства опиралась на ошибочный вариант программы CARAT.
  23. ↑ E. J. W. Whittaker, An atlas of hyperstereograms of the four-dimensional crystal classes. Clarendon Press (Oxford Oxfordshire and New York) 1985.
  24. ↑ H. Brown, R. Bülow, J. Neubüser, H. Wondratschek and H. Zassenhaus, Crystallographic Groups of Four-Dimensional Space. Wiley, NY, 1978.

Ссылки

Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Сингония&oldid=5818768