Азимут

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
(перенаправлено с «Азимут (астрономия)»)
Для термина «Азимут» см. также другие значения.
Демонстрация принципа азимута

А́зимут (от араб. سمت‎ симт — направление, путь, цель; араб. السمت‎ ас-симт, или араб. السموت‎ ас-самут — азимут[1], обозначается «Аз» или «Az») — горизонтальный угол, отсчитываемый между заранее выбранным направлением (например, северным) и направлением на заданный предмет. Азимут обычно отсчитывается по часовой стрелке от выбранного начального направления, однако допускает различные определения, как по начальному направлению, так и по направлению самого отсчёта (влево или вправо от начального направления). Дирекционный угол, румб и пр. углы ориентирования являются частными случаями азимута.

Это понятие используется в навигации, астрономии, инжиниринге, картографии, добывающей промышленности и баллистике.

Cистемы счёта азимутов

Круговой азимут измеряется всегда от точки N (С, север) в сторону точки E (В, восток), то есть по часовой стрелке от 0 до 360°. При записи азимута в круговом счёте его наименование не указывается: А = 120° (за рубежом — Zn)[2].

При полукруговом счёте азимут измеряется от северной или южной части меридиана наблюдателя в сторону E (В, восток) или W (З, запад) от 0° до 180°[3]. При полукруговом счёте указывается направление отсчёта E (В, восток) или W (З, запад). В разных традициях отсчёт положительных или отрицательных углов производится по-разному: против часовой стрелки или по часовой стрелке.

При квадрантном (четвертькруговом) счёте азимут измеряется от северной или южной части меридиана наблюдателя в сторону E (В, восток) или W (З, запад) от 0° до 90°. При четвертькруговом счёте указывается направление отсчёта NE (СВ, северо-восток), NW (СЗ, северо-запад), SE (ЮВ, юго-восток), SW (ЮЗ, юго-запад).

Также круговой азимут называют полным или цельным, а некруговые (полукруговой и четвертькруговой) — дифференцированными.

Направление Круговой азимут Полукруговой азимут (против часовой стрелки «+») Четвертькруговой азимут
север 0° или 360° С 0° или Ю ±180° С 0°
северо-восток 45° В −45° или З +135° СВ 45°
восток 90° В ±90° СВ или ЮВ 90°
юго-восток 135° В −135° или З +45° ЮВ 45°
юг 180° С ±180° или Ю 0° Ю 0°
юго-запад 225° В +135° или 3 −45° ЮЗ 45°
запад 270° 3 ±90° СЗ или ЮЗ 90°
северо-запад 315° В −135° или З +45° СЗ 45°

Виды азимута

Различают неориентированные и ориентированные азимуты. Последние подразделяются на географический (истинный), магнитный, прямой и обратный.

Если за исходное направление принимается географический меридиан, азимут называется истинным; если за исходное направление принимается магнитный меридиан, азимут называется магнитным.

Углы TB1 и ТB 2 — углы пеленга. RB1 и RB2 — азимуты или курсовые углы двух объектов

Абсолютные азимуты

Абсолютные азимуты отсчитываются от направления на абстрактный объект (например, полюс). К абсолютным азимутам относятся пеленг и румб. Истинные направления проходят через точку стояния и географические или магнитные полюса Земли (северный или южный). Измеряются строго по часовой стрелке[4].

Магнитный азимут Am — горизонтальный физический угол, измеренный по ходу часовой стрелки от северного направления стрелки компаса до направления на предмет (воображаемой линии). Магнитный азимут определяется при помощи компаса. Его значения могут быть от 0° до 360°. Магнитный азимут всегда прямой[4].

Географический азимут Ag или дирекционный угол — горизонтальный математический угол, отсчитываемый от северного направления меридиана по ходу часовой стрелки до ориентируемой линии. Изменяется от 0 до 360°[5].

Основная статья: Дирекционный угол

Географический азимут направления определяется с помощью транспортира по топографическим картам (планам) или по аэроснимкам. При этом 0 транспортира устанавливается в направлении на север и берётся угловой отсчёт по направлению на заданный объект. Может быть прямым и обратным. Обратный азимут — азимут направления, противоположного определяемому (прямому), отличается от прямого азимута на 180°.

Для перехода от магнитного меридиана к истинному нужно знать магнитное склонение в точке наблюдения. Величина магнитного склонения указывается на многих картах.

Зная склонение магнитной стрелки и имея компас и два ориентира (опознанные характерные точки на карте и местности), можно приблизительно определить магнитный азимут, а затем и дирекционный угол. По значению магнитного азимута направления ([math]\displaystyle{ A_m }[/math]), измеренного с помощью компаса и карты сориентированной по двум наблюдаемым ориентирам. Путём ввода в полученное измерение (магнитного азимута) поправки направления (значение, обратное склонению магнитной стрелки " — " [math]\displaystyle{ \gamma }[/math]), взятое с топографической карты на дату наблюдений. Может быть с точностью порядка 0,5-3 угловых градуса определен дирекционный угол направления ([math]\displaystyle{ \alpha }[/math]) на местности. [math]\displaystyle{ \alpha=A_m-\gamma. }[/math]

Геодезический азимут

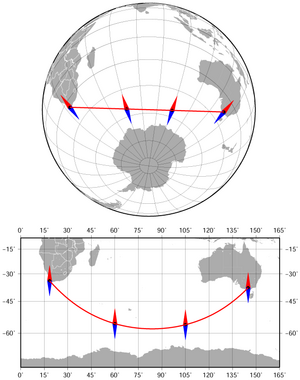
Азимут между Кейптауном и Мельбурном вдоль кратчайшего пути (геодезической) меняется от 141° до 42°. Ортографическая проекция и Цилиндрическая проекция Миллера

Геодезический азимут — это двугранный угол между плоскостью меридиана и вертикальной плоскостью, проходящей через нормаль, отсчитываемой от направления на север по ходу часовой стрелки от 0° до 360°. Устанавливает связь между дирекционным углом и плоскостью, проходящей через отвесную линию[6][7][8].

Для перехода от астрономического азимута к геодезическому служит формула[8].

[math]\displaystyle{ A = a - h\operatorname{tg} \varphi - (x\sin a - h\cos a)\cdot \operatorname{ctg} z, }[/math]

в которой [math]\displaystyle{ x }[/math] и [math]\displaystyle{ h }[/math] — составляющие отклонения отвеса в пункте наблюдения в плоскостях меридиана и первого вертикала, [math]\displaystyle{ \varphi }[/math] — широта этого пункта и [math]\displaystyle{ z }[/math] — зенитное расстояние наблюдаемой точки в пространстве. Эта формула при [math]\displaystyle{ z }[/math], близком к 90°, приводит к уравнению Лапласа: [math]\displaystyle{ A = a - h\operatorname{tg} \varphi }[/math][8].

Азимут Лапласа

Азимут Лапласа — геодезический азимут, полученный по астрономическому азимуту [math]\displaystyle{ a }[/math] и исправленный с учётом влияния отклонения отвеса[8][9][10][11].

Астрономический азимут

Азимутом светила называется дуга математического горизонта от точки юга до вертикального круга светила, или угол между полуденной линией и линией пересечения плоскости математического горизонта с вертикальной плоскостью, проходящей через линию направления на светило.

Астрономические азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. Светила, находящиеся на одном вертикальном круге, имеют одинаковые азимуты.

Следует отметить различие между геодезическим и астрономическим определениями азимута. В отличие от астрономии, в геодезии азимуты отсчитываются от точки севера на восток (т. е. в том же направлении, но с отличием на 180°[12][13][8].

Геологические азимуты

Навигационные азимуты

Пеленг

Основная статья: Пеленг (навигация)

Пеленг — горизонтальный угол между северной частью меридиана наблюдателя и направлением из точки наблюдения на объект; измеряется по часовой стрелке от нуля (строго направление на север, N) до полной дуги окружности (от 0° до 360°)[14].

Румб

Основные статьи: Румб (геодезия) и Румб

Румб — горизонтальный угол между ориентирным направлением меридиана и направлением на объект; измеряется по часовой стрелке или против. Ориентирные направления меридиана и диапазон отсчитываемых углов, могут существенно отличаться друг от друга.

Относительные азимуты

Относительные азимуты отсчитываются от направления движения или от другого выбранного направления, важного для решаемой задачи.

Навигация и геодезия

Курсовой угол или относительный пеленг

Основные статьи: Курсовой угол и Траверз

Курсовой угол — угол между диаметральной плоскостью судна (осью) и направлением на предмет. Отсчёт курсовых углов производится круговым счётом от носовой части судна по часовой стрелке от 0 до 360° или полукруговым счётом от 0 до 180° от носовой части судна в сторону борта, по которому расположен предмет[15].

Курсовой угол в 90° (к правому или левому борту) называется траверзом.

См. также

Примечания

  1. ↑ Баранов Х. К. Арабско-русский словарь: Ок. 42 000 слов / Под ред. В. А. Костина. — М., 2001. — С. 372. — 944 с. — ISBN 5-901278-01-1.
  2. ↑ Сферические координаты светил. Дата обращения: 29 сентября 2019. Архивировано 27 декабря 2018 года.
  3. ↑ 3. Мореходная астрономия. Дата обращения: 29 сентября 2019. Архивировано 29 сентября 2019 года.
  4. ↑ 4,0 4,1 Лахин А. Ф., Бызов Б. Е., Прищепа И. М. Военная топография для курсантов учебных подразделений. — Москва: Военное издательство Министерства обороны СССР, 1973. — С. 49—50. — 224 с.
  5. ↑ [неавторитетный источник?] ОРИЕНТИРОВАНИЕ. ИСТИННЫЕ (географические) АЗИМУТЫ, ПРЯМОЙ И ОБРАТНЫЙ АЗИМУТЫ, СБЛИЖЕНИЕ МЕРИДИАНОВ. РУМБЫ.. Дата обращения: 25 сентября 2019. Архивировано 25 сентября 2019 года.
  6. ↑ ГОСТ 22268-76 п.57
  7. ↑ «Геодезический азимут». Дата обращения: 24 января 2020. Архивировано 12 октября 2019 года.
  8. ↑ 8,0 8,1 8,2 8,3 8,4 Лапласа азимут : Энциклопедия БСЭ - alcala.ru. Дата обращения: 24 января 2020. Архивировано 24 января 2020 года.
  9. ↑ Азимуты Лапласа. Дата обращения: 24 января 2020. Архивировано 2 февраля 2020 года.
  10. ↑ Предмет и задачи геодезической астрономии. Дата обращения: 27 января 2020. Архивировано 27 января 2020 года.
  11. ↑ С. С. Уралов. § 1. Предмет и задачи геодезической астрономии // Курс геодезической астрономии. — Москва: Недра, 1980. — С. 5. — 592 с.
  12. ↑ Энциклопедический словарь юного астронома/ Ред. коллегия, Ерпылев Н. П. (сост.) и др. — 2-е изд., перераб. и доп. — М.: Педагогика, 1986. — С. 189—192 — 336 с. Архивная копия от 27 февраля 2021 на Wayback Machine
  13. ↑ Артиллерия. — М.: Воениздат МО СССР, 1953.. Дата обращения: 1 февраля 2020. Архивировано 24 января 2020 года.
  14. ↑ ГОСТ 23634-83. Дата обращения: 28 мая 2020. Архивировано 30 сентября 2020 года.
  15. ↑ § 8. Истинный курс. Истинный пеленг. Курсовой угол. Дата обращения: 27 сентября 2019. Архивировано 27 сентября 2019 года.

Литература

Ссылки

Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Азимут&oldid=18410703#Астрономический_азимут