Спорадическая группа

Спорадическая группа — одна из 26 исключительных групп в теореме о классификации простых конечных групп.

Простая группа — это группа G, не содержащая каких-либо нормальных подгрупп, отличных от самой группы G и тривиальной (единичной) подгруппы. Теорема классификации утверждает, что список конечных простых групп состоит из 18 счётных бесконечных семейств, плюс 26 исключений, которые не попадают в эту классификацию. Эти исключения называются спорадическими группами. Они также известны под названиями «спорадические простые группы» или «спорадические конечные группы». Поскольку группа Титса не является строго группой лиева типа, иногда она также считается спорадической и в этом случае является 27-ой спорадической группой.

Группа Монстр является наибольшей среди спорадических групп и содержит в качестве подгрупп или подфакторгрупп все, за исключением шести, другие спорадические группы.

Имена спорадических групп

Пять спорадических групп обнаружил Матьё в 1860-х годах, остальные 21 найдены между 1965 и 1975 годами. Существование нескольких из этих групп было предсказано до их построения. Позднее было доказано, что этим окончательно завершён полный поиск. Большинство групп носят имена математиков, первыми предсказавшими их существование.

Полный список групп:

Диаграмма показывает подфакторные связи спорадических групп.

• группы Матьё M₁₁, M₁₂, M₂₂, M₂₃, M₂₄
• группы Янко J₁, J₂ или HJ, J₃ или HJM, J₄
• Группы Конвея Co₁, Co₂, Co₃
• Группы Фишера Fi₂₂, Fi₂₃, Fi₂₄′ или F₃₊
• Группа Хигмана — Симса HS
• Группа МакЛафлина McL
• Группа Хельда He или F₇₊, или F₇
• Группа Рудвалиса Ru
• Группа Судзуки Suz или F₃₋
• Группа О'Нана O’N
• Группа Харады — Нортона HN или F₅₊, или F₅
• Группа Лайонса Ly
• Группа Томпсона Th или F_3|3, или F₃
• Группа «малый Монстр» B или F₂₊, или F₂
• Группа «Монстр» Фишера-Грейса M или F₁

Группа Титса T иногда также считается спорадической группой (она почти лиева типа) и по этой причине по некоторым источникам число спорадических групп даётся как 27, а не 26. По другим источникам группа Титса не считается ни спорадической, ни группой лиева типа.

Для всех спорадических групп были построены матричные представления над конечными полями.

Наиболее раннее употребление термина «спорадическая группа» найдено у Бёрнсайда, где он говорит о группах Матьё: «Эти, по всей видимости, спорадические простые группы требуют более тщательного исследования, чем до сих пор получали».

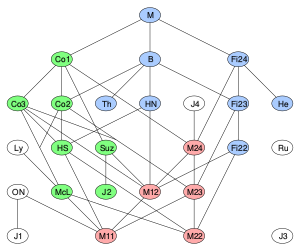
Диаграмма справа основывается на диаграмме Ронана. Спорадические группы также имеют большое число подгрупп, не являющихся спорадическими, но на диаграмме они не представлены ввиду их огромного числа.

Система

Из 26 спорадических групп 20 находятся внутри группы «Монстр» в качестве подгрупп или подфакторгрупп.

I. Парии

Основная статья: Парии (теория групп)

Шесть исключений J₁, J₃, J₄, O’N, Ru и Ly иногда называют париями.

II. Счастливое Семейство

Остальные двадцать групп называют Счастливым семейством (название дал Роберт Грис) и их можно разбить на три поколения.

Первое поколение (5 групп) — группы Матьё

Основная статья: Группа Матьё

Группы M_n для n = 11, 12, 22, 23 и 24 являются кратно-транзитивными группами перестановок n точек. Все они являются подгруппами группы M₂₄, которая является группой перестановок 24 точек.

Второе поколение (7 групп) — решётка Лича

См. также: Решётка Лича и Группы Конвея

Все подфакторы группы автоморфизмов решётки в 24-мерном пространстве, называемой решёткой Лича:

• Co₁ — факторгруппа группы автоморфизмов по центру {±1}
• Co₂ — стабилизатор вектора типа 2 (то есть длины 2)
• Co₃ — стабилизатор вектора типа 3 (то есть длины √6)
• Suz — группа автоморфизмов, сохраняющих структуру (модуль центра)
• McL — стабилизатор треугольника типа 2-2-3
• HS — стабилизатор треугольника типа 2-3-3
• J₂ — группа автоморфизмов, сохраняющих кватернионную структуру (модуль по центру).

Третье поколение (8 групп) — другие подгруппы Монстра

Состоит из подгрупп, которые тесно связаны с Монстром M:

• B или F₂ имеет двойное покрытие, являющееся централизатором элемента порядка 2 в M
• Fi₂₄′ имеет тройное покрытие, являющееся централизатором элемента порядка 3 в M (класс сопряжённости «3A»)
• Fi₂₃ является подгруппой Fi₂₄′
• Fi₂₂ имеет двойное покрытие, которое является подгруппой Fi₂₃
• Произведение Th = F₃ и группы порядка 3 является централизатором элемента порядка 3 в M (класс сопряжённости «3C»)
• Произведение HN = F₅ и группы порядка 5 является централизатором элемента порядка 5 в M
• Произведение He = F₇ и группы порядка 7 является централизатором элемента порядка 7 в M.
• Наконец, Монстр сам по себе считается принадлежащим этому поколению.

(Эта серия продолжается и дальше — произведение M₁₂ и группы порядка 11 является централизатором элемента порядка 11 в M.)

Группа Титса также принадлежит этому поколению — существует подгруппа [math]\displaystyle{ S_4 \times {^2}{F_4(2)^\prime} }[/math], нормализующая 2C² подгруппу B, порождающая подгруппу [math]\displaystyle{ 2{\cdot}S_4 \times {^2}F_4(2)^\prime }[/math], нормализующую некоторую подгруппу Q₈ Монстра. [math]\displaystyle{ {^2}F_4(2)^\prime }[/math] является также подгруппой групп Фишера Fi₂₂, Fi₂₃ и Fi₂₄′ и «малого Монстра» B. [math]\displaystyle{ {^2}F_4(2)^\prime }[/math] является подгруппой группы-парии Рудвалиса Ru и не имеет других зависимостей со спорадическими простыми группами кроме перечисленных выше.

Таблица порядков спорадических групп

Группа	Поколение	Порядок (последовательность A001228 в OEIS)	Значащих цифр	Разложение	Тройка Стандартных генераторов (a, b, ab)	Другие условия
F1 или M	третье	8080174247945128758864599049617107 57005754368000000000	≈ 8⋅1053	246 • 320 • 59 • 76 • 112 • 133 • 17 • 19 • 23 • 29 • 31 • 41 • 47 • 59 • 71	2A, 3B, 29
F2 или B	третье	4154781481226426191177580544000000	≈ 4⋅1033	[math]\displaystyle{ 2^{41} \cdot 3^{13} \cdot 5^6 \cdot 7^2 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot 31 \cdot 47 }[/math]	2C, 3A, 55	[math]\displaystyle{ o((ab)^2 (abab^2)^2 ab^2) = 23 }[/math]
Fi24' или F3+	третье	1255205709190661721292800	≈ 1⋅1024	221 • 316 • 52 • 73 • 11 • 13 • 17 • 23 • 29	2A, 3E, 29	[math]\displaystyle{ o((ab)^3 b) = 33 }[/math]
Fi23	третье	4089470473293004800	≈ 4⋅1018	218 • 313 • 52 • 7 • 11 • 13 • 17 • 23	2B, 3D, 28
Fi22	третье	64561751654400	≈ 6⋅1013	217 • 39 • 52 • 7 • 11 • 13	2A, 13, 11	[math]\displaystyle{ o((ab)^2 (abab^2)^2 ab^2) = 12 }[/math]
F3 или Th	третье	90745943887872000	≈ 9⋅1016	215 • 310 • 53 • 72 • 13 • 19 • 31	2, 3A, 19
Ly	пария	51765179004000000	≈ 5⋅1016	28 • 37 • 56 • 7 • 11 • 31 • 37 • 67	2, 5A, 14	[math]\displaystyle{ o(ababab^2) = 67 }[/math]
F5 или HN	третье	273030912000000	≈ 3⋅1014	214 • 36 • 56 • 7 • 11 • 19	2A, 3B, 22	[math]\displaystyle{ o([a, b]) = 5 }[/math]
Co1	второе	4157776806543360000	≈ 4⋅1018	221 • 39 • 54 • 72 • 11 • 13 • 23	2B, 3C, 40
Co2	второе	42305421312000	≈ 4⋅1013	218 • 36 • 53 • 7 • 11 • 23	2A, 5A, 28
Co3	второе	495766656000	≈ 5⋅1011	210 • 37 • 53 • 7 • 11 • 23	2A, 7C, 17
O'N	пария	460815505920	≈ 5⋅1011	29 • 34 • 5 • 73 • 11 • 19 • 31	2A, 4A, 11
Suz	второе	448345497600	≈ 4⋅1011	213 • 37 • 52 • 7 • 11 • 13	2B, 3B, 13	[math]\displaystyle{ o([a, b]) = 15 }[/math]
Ru	пария	145926144000	≈ 1⋅1011	214 • 33 • 53 • 7 • 13 • 29	2B, 4A, 13
F7 или He	третье	4030387200	≈ 4⋅109	210 • 33 • 52 • 73 • 17	2A, 7C, 17
McL	второе	898128000	≈ 9⋅108	27 • 36 • 53 • 7 • 11	2A, 5A, 11	[math]\displaystyle{ o((ab)^2 (abab^2)^2 ab^2) = 7 }[/math]
HS	второе	44352000	≈ 4⋅107	29 • 32 • 53 • 7 • 11	2A, 5A, 11
J4	пария	86775571046077562880	≈ 9⋅1019	221 • 33 • 5 • 7 • 113 • 23 • 29 • 31 • 37 • 43	2A, 4A, 37	[math]\displaystyle{ o(abab^2) = 10 }[/math]
J3 или HJM	пария	50232960	≈ 5⋅107	27 • 35 • 5 • 17 • 19	2A, 3A, 19	[math]\displaystyle{ o([a, b]) = 9 }[/math]
J2 или HJ	второе	604800	≈ 6⋅105	27 • 33 • 52 • 7	2B, 3B, 7	[math]\displaystyle{ o([a, b]) = 12 }[/math]
J1	пария	175560	≈ 2⋅105	23 • 3 • 5 • 7 • 11 • 19	2, 3, 7	[math]\displaystyle{ o(abab^2) = 19 }[/math]
M24	первое	244823040	≈ 2⋅108	210 • 33 • 5 • 7 • 11 • 23	2B, 3A, 23	[math]\displaystyle{ o(ab(abab^2)^2 ab^2) = 4 }[/math]
M23	первое	10200960	≈ 1⋅107	27 • 32 • 5 • 7 • 11 • 23	2, 4, 23	[math]\displaystyle{ o((ab)^2 (abab^2)^2 ab^2) = 8 }[/math]
M22	первое	443520	≈ 4⋅105	27 • 32 • 5 • 7 • 11	2A, 4A, 11	[math]\displaystyle{ o(abab^2) = 11 }[/math]
M12	первое	95040	≈ 1⋅105	26 • 33 • 5 • 11	2B, 3B, 11
M11	первое	7920	≈ 8⋅103	24 • 32 • 5 • 11	2, 4, 11	[math]\displaystyle{ o((ab)^2 (abab^2)^2 ab^2) = 4 }[/math]

Литература

• William Burnside. Theory of groups of finite order. — 1911. — С. 504 (note N). — ISBN 0-486-49575-2.
• Conway J. H. A perfect group of order 8,315,553,613,086,720,000 and the sporadic simple groups // Proc. Natl. Acad. Sci. U.S.A.. — 1968. — Т. 61, вып. 2. — С. 398–400. — doi:10.1073/pnas.61.2.398.
• Conway J. H., Curtis R. T., Norton S. P., Wilson R. A. Atlas of finite groups. Maximal subgroups and ordinary characters for simple groups. With computational assistance from J. G. Thackray. — Oxford University Press, 1985. — ISBN 0-19-853199-0.
• Gorenstein D., Lyons R., Solomon R. The Classification of the Finite Simple Groups. — American Mathematical Society, 1994. Выпуски 1, 2, …
• Robert L. Griess. Twelve Sporadic Groups. — Springer-Verlag, 1998. — ISBN 3540627782.
• Mark Ronan. Symmetry and the Monster. — Oxford, 2006. — ISBN 978-0-19-280722-9.

Ссылки

• Weisstein, Eric W. Sporadic Group (англ.) на сайте Wolfram MathWorld.
• Atlas of Finite Group Representations: Sporadic groups