Диэдральная группа

Диэдральная группа (группа диэдра) — группа симметрии правильного многоугольника, включающая как вращения, так и осевые симметрии[1]. Диэдральные группы являются простейшими примерами конечных групп и играют важную роль в теории групп, геометрии и химии. Хорошо известно и совершенно тривиально проверяется, что группа, образованная двумя инволюциями с конечным числом элементов в области определения является диэдральной группой.
Обозначения
Имеется два основных вида записи диэдральной группы, связанной с [math]\displaystyle{ n }[/math]-сторонним многоугольником. В геометрии группа записывается как [math]\displaystyle{ \mathrm{D}_n }[/math], в то время как в общей алгебре та же самая группа обозначается как [math]\displaystyle{ \mathrm{D}_{2n} }[/math], где индекс является числом элементов в группе. Имеется также нотация Коксетера, в которой осевая симметрия порядка [math]\displaystyle{ 2n }[/math] обозначается как [math]\displaystyle{ [n] }[/math]), а вращение порядка [math]\displaystyle{ n }[/math] как [math]\displaystyle{ [n]^+ }[/math]. Ещё одна запись — нотация орбиобразия, в которой осевая симметрия обозначается как [math]\displaystyle{ *nn }[/math], а вращения — как [math]\displaystyle{ n }[/math].
В этой статье [math]\displaystyle{ \mathrm{D}_n }[/math] (или, иногда, [math]\displaystyle{ \mathrm{Dih}_n }[/math]) относится к симметриям правильного [math]\displaystyle{ n }[/math]-угольника.
Определение
Элементы

Правильный [math]\displaystyle{ n }[/math]-угольник имеет [math]\displaystyle{ 2n }[/math] различных симметрий: [math]\displaystyle{ n }[/math] поворотов и [math]\displaystyle{ n }[/math] осевых отражений, образующих диэдральную группу [math]\displaystyle{ \mathrm{D}_n }[/math]. Если [math]\displaystyle{ n }[/math] нечётно, каждая ось симметрии проходит через середину одной из сторон и противоположную вершину. Если [math]\displaystyle{ n }[/math] чётно, имеется [math]\displaystyle{ n/2 }[/math] осей симметрии, соединяющих середины противоположных сторон и [math]\displaystyle{ n/2 }[/math] осей, соединяющих противоположные вершины. В любом случае, имеется [math]\displaystyle{ n }[/math] осей симметрии и [math]\displaystyle{ 2n }[/math] элементов в группе симметрий. Отражение относительно одной оси, а затем относительно другой, приводит к вращению на удвоенный угол между осями. Изображения ниже показывают результат действия элемента [math]\displaystyle{ \mathrm{D}_8 }[/math] на дорожный знак Стоп:
Первая строка показывает восемь вращений, а вторая — восемь отражений.
Структура группы
Как и для любого другого геометрического объекта, композиция двух симметрий правильного многоугольника снова будет симметрией. Таким образом, симметрии правильного многоугольника образуют конечную группу.


Таблица Кэли показывает результаты композиций в группе [math]\displaystyle{ \mathrm{D}_3 }[/math] симметрий правильного треугольника. [math]\displaystyle{ \mathrm{R}_0 }[/math] обозначает тождественное преобразование, [math]\displaystyle{ \mathrm{R}_1 }[/math] и [math]\displaystyle{ \mathrm{R}_2 }[/math] обозначают вращение против часовой стрелки на [math]\displaystyle{ 120 }[/math] и [math]\displaystyle{ 240 }[/math] градусов соответственно, [math]\displaystyle{ \mathrm{S}_0 }[/math], [math]\displaystyle{ \mathrm{S}_1 }[/math], и [math]\displaystyle{ \mathrm{S}_2 }[/math] обозначают отражения относительно осей, показанных на рисунке справа.
| [math]\displaystyle{ \mathrm{R}_0 }[/math] | [math]\displaystyle{ \mathrm{R}_1 }[/math] | [math]\displaystyle{ \mathrm{R}_2 }[/math] | [math]\displaystyle{ \mathrm{S}_0 }[/math] | [math]\displaystyle{ \mathrm{S}_1 }[/math] | [math]\displaystyle{ \mathrm{S}_2 }[/math] | |
|---|---|---|---|---|---|---|
| [math]\displaystyle{ \mathrm{R}_0 }[/math] | [math]\displaystyle{ \mathrm{R}_0 }[/math] | [math]\displaystyle{ \mathrm{R}_1 }[/math] | [math]\displaystyle{ \mathrm{R}_2 }[/math] | [math]\displaystyle{ \mathrm{S}_0 }[/math] | [math]\displaystyle{ \mathrm{S}_1 }[/math] | [math]\displaystyle{ \mathrm{S}_2 }[/math] |
| [math]\displaystyle{ \mathrm{R}_1 }[/math] | [math]\displaystyle{ \mathrm{R}_1 }[/math] | [math]\displaystyle{ \mathrm{R}_2 }[/math] | [math]\displaystyle{ \mathrm{R}_0 }[/math] | [math]\displaystyle{ \mathrm{S}_1 }[/math] | [math]\displaystyle{ \mathrm{S}_2 }[/math] | [math]\displaystyle{ \mathrm{S}_0 }[/math] |
| [math]\displaystyle{ \mathrm{R}_2 }[/math] | [math]\displaystyle{ \mathrm{R}_2 }[/math] | [math]\displaystyle{ \mathrm{R}_0 }[/math] | [math]\displaystyle{ \mathrm{R}_1 }[/math] | [math]\displaystyle{ \mathrm{S}_2 }[/math] | [math]\displaystyle{ \mathrm{S}_0 }[/math] | [math]\displaystyle{ \mathrm{S}_1 }[/math] |
| [math]\displaystyle{ \mathrm{S}_0 }[/math] | [math]\displaystyle{ \mathrm{S}_0 }[/math] | [math]\displaystyle{ \mathrm{S}_2 }[/math] | [math]\displaystyle{ \mathrm{S}_1 }[/math] | [math]\displaystyle{ \mathrm{R}_0 }[/math] | [math]\displaystyle{ \mathrm{R}_2 }[/math] | [math]\displaystyle{ \mathrm{R}_1 }[/math] |
| [math]\displaystyle{ \mathrm{S}_1 }[/math] | [math]\displaystyle{ \mathrm{S}_1 }[/math] | [math]\displaystyle{ \mathrm{S}_0 }[/math] | [math]\displaystyle{ \mathrm{S}_2 }[/math] | [math]\displaystyle{ \mathrm{R}_1 }[/math] | [math]\displaystyle{ \mathrm{R}_0 }[/math] | [math]\displaystyle{ \mathrm{R}_2 }[/math] |
| [math]\displaystyle{ \mathrm{S}_2 }[/math] | [math]\displaystyle{ \mathrm{S}_2 }[/math] | [math]\displaystyle{ \mathrm{S}_1 }[/math] | [math]\displaystyle{ \mathrm{S}_0 }[/math] | [math]\displaystyle{ \mathrm{R}_2 }[/math] | [math]\displaystyle{ \mathrm{R}_1 }[/math] | [math]\displaystyle{ \mathrm{R}_0 }[/math] |
Например, [math]\displaystyle{ \mathrm{S}_2\mathrm{S}_1 = \mathrm{R}_1 }[/math], поскольку применение последовательно отражений [math]\displaystyle{ \mathrm{S}_1 }[/math] и [math]\displaystyle{ \mathrm{S}_2 }[/math] даёт поворот на [math]\displaystyle{ 120^\circ }[/math]. Обратите внимание на то, что композиция не является коммутативной операцией.
В общем случае, группа [math]\displaystyle{ \mathrm{D}_n }[/math] содержит элементы [math]\displaystyle{ \mathrm{R}_0,\dots\mathrm{R}_{n-1} }[/math] и [math]\displaystyle{ \mathrm{S}_0,\dots\mathrm{S}_{n-1} }[/math] и в качестве операции имеет композицию, которая задается формулами:
- [math]\displaystyle{ \mathrm{R}_i\mathrm{R}_j = \mathrm{R}_{i+j} }[/math]
- [math]\displaystyle{ \mathrm{S}_i\mathrm{R}_j = \mathrm{S}_{i-j} }[/math]
- [math]\displaystyle{ \mathrm{R}_i\mathrm{S}_j = \mathrm{S}_{i+j} }[/math]
- [math]\displaystyle{ \mathrm{S}_i\mathrm{S}_j = \mathrm{R}_{i-j} }[/math]
Во всех случаях сложение и вычитание индексов должно выполняться с использованием вычетов по модулю [math]\displaystyle{ n }[/math].
Матричное представление

Если расположить центр правильного многоугольника в начале координат, элементы диэдральной группы станут линейными отображениями плоскости. Это позволяет представить элементы [math]\displaystyle{ \mathrm{D}_n }[/math] как группу матриц, с умножением матриц в качестве операции композиции. Такое представление является примером [math]\displaystyle{ 2 }[/math]-мерного представления группы.
Рассмотрим в качестве примера элементы группы [math]\displaystyle{ \mathrm{D}_4 }[/math]. Их можно представить как [math]\displaystyle{ 8 }[/math] следующих матриц:
- [math]\displaystyle{ \begin{matrix} R_0=\bigl(\begin{smallmatrix}1&0\\[0.2em]0&1\end{smallmatrix}\bigr), & R_1=\bigl(\begin{smallmatrix}0&-1\\[0.2em]1&0\end{smallmatrix}\bigr), & R_2=\bigl(\begin{smallmatrix}-1&0\\[0.2em]0&-1\end{smallmatrix}\bigr), & R_3=\bigl(\begin{smallmatrix}0&1\\[0.2em]-1&0\end{smallmatrix}\bigr), \\[1em] S_0=\bigl(\begin{smallmatrix}1&0\\[0.2em]0&-1\end{smallmatrix}\bigr), & S_1=\bigl(\begin{smallmatrix}0&1\\[0.2em]1&0\end{smallmatrix}\bigr), & S_2=\bigl(\begin{smallmatrix}-1&0\\[0.2em]0&1\end{smallmatrix}\bigr), & S_3=\bigl(\begin{smallmatrix}0&-1\\[0.2em]-1&0\end{smallmatrix}\bigr). \end{matrix} }[/math]
В общем случае, матрицы для элементов [math]\displaystyle{ \mathrm{D}_n }[/math] имеют следующий вид:
- [math]\displaystyle{ \begin{align} R_k & = \begin{pmatrix} \cos \frac{2\pi k}{n} & -\sin \frac{2\pi k}{n} \\ \sin \frac{2\pi k}{n} & \cos \frac{2\pi k}{n} \end{pmatrix} \ \ \text{и} \\ S_k & = \begin{pmatrix} \cos \frac{2\pi k}{n} & \sin \frac{2\pi k}{n} \\ \sin \frac{2\pi k}{n} & -\cos \frac{2\pi k}{n} \end{pmatrix}. \end{align} }[/math]
Здесь [math]\displaystyle{ \mathrm{R}_k }[/math] — это матрица поворота против часовой стрелки на угол [math]\displaystyle{ \frac{2\pi k}{n} }[/math], а [math]\displaystyle{ \mathrm{S}_k }[/math] — отражение относительно оси, образующей угол [math]\displaystyle{ \frac{\pi k}{n} }[/math] с осью абсцисс.
Маленькие диэдральные группы
Для [math]\displaystyle{ n=1 }[/math] получим [math]\displaystyle{ \mathrm{Dih}_1 }[/math]. Это обозначение используется редко, разве что для обозначении в последовательности других групп, поскольку группа эквивалентна [math]\displaystyle{ Z_2 }[/math].
Для [math]\displaystyle{ n=2 }[/math] получим [math]\displaystyle{ \mathrm{Dih}_2 }[/math] — четверную группу Клейна.
Оба случая являются исключениями в серии:
- Они абелевы, в то время как для всех остальных [math]\displaystyle{ n }[/math] группа [math]\displaystyle{ \mathrm{Dih}_n }[/math] не абелева.
- Они не являются подгруппами симметрической группы [math]\displaystyle{ \mathrm{S}_n }[/math], поскольку [math]\displaystyle{ 2n\gt n! }[/math] для этих [math]\displaystyle{ n }[/math].
Граф циклов диэдральных групп состоит из одного цикла длины [math]\displaystyle{ n }[/math] и [math]\displaystyle{ n }[/math] циклов длины [math]\displaystyle{ 2 }[/math]. Темные вершины графа циклов ниже показывают тождественное преобразование, белые — остальные элементы группы. Цикл состоит из последовательных степеней остальных элементов.
|
 |
 |
Диэдральная группа как группа симметрии в 2D и группа вращений в 3D
Примером абстрактной группы Dihn и общепринятого пути графического представления является группа Dn изометрий плоскости, не двигающих начало координат. Эти группы формируют одну из двух серий дискретных групп точек на плоскости. Dn состоит из n вращений на угол, кратный 360°/n, вокруг начала координат, и отражений относительно n осей, проходящих через центр координат и углом к остальным осям, кратным 180°/n. Эти точки представляют группу симметрии правильного многоугольника с n сторонами (для n ≥ 3).
Диэдральная группа Dn is порождается вращением r порядка n и отражением s порядка 2, такими что
- [math]\displaystyle{ srs = r^{-1} }[/math]
В терминах геометрии: зеркальное отражение вращения выглядит как обратное вращение.
В терминах комплексных чисел: умножением на [math]\displaystyle{ e^{2\pi i \over n} }[/math] и сопряжением.
В терминах матриц: задав
- [math]\displaystyle{ r_1 = \begin{bmatrix}\cos{2\pi \over n} & -\sin{2\pi \over n} \\[8pt] \sin{2\pi \over n} & \cos{2\pi \over n}\end{bmatrix} \qquad s_0 = \begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix} }[/math]
и определив [math]\displaystyle{ r_j = r_1^j }[/math] и [math]\displaystyle{ s_j = r_j \, s_0 }[/math] для [math]\displaystyle{ j \in \{1,\ldots,n-1\} }[/math] мы можем записать правила образования Dn как
- [math]\displaystyle{ r_j \, r_k = r_{(j+k) \text{ mod }n} }[/math]
- [math]\displaystyle{ r_j \, s_k = s_{(j+k) \text{ mod }n} }[/math]
- [math]\displaystyle{ s_j \, r_k =s_{(j-k) \text{ mod }n} }[/math]
- [math]\displaystyle{ s_j \, s_k = r_{(j-k) \text{ mod }n}. }[/math]
(Сравните Матрица поворота.)
Диэдральная группа D2 порождается вращением r на 180 градусов, и симметрией s относительно оси X. Элементы D2 можно представить как {e, r, s, rs}, где e — тождественное преобразование и rs — симметрия относительно оси 'Y.

D2 изоморфна четверной группе Клейна.
Для n>2 операции вращения и отражения относительно прямой не коммутативны и Dn не является абелевой. Например, в D4, вращение 90 градусов, а затем отражение дает совсем другой результат, нежели отражение, а затем вращение.

Таким образом, наряду с очевидным приложением к проблемам симметрии на плоскости, эти группы служат простейшими примерами неабелевых групп, и часто используются как контрпримеры для теорем, ограниченных абелевыми группами.
2n элементов Dn можно записать как e, r, r2, …, rn−1, s, r s, r2 s, …, rn−1 s. Первые n перечисленных элементов являются вращениями, остальные n — отражения относительно осей (все они имеют порядок 2). Результатом двух вращений или двух отражений будет вращение Результат вращения и отражения будет отражением.
Таким образом, мы установили, что Dn является подгруппой O(2).
Однако, обозначение Dn используется для подгрупп SO(3), которые тоже являются группами типа Dihn: группа симметрии многоугольника, вложенного в трехмерное пространство (если n ≥ 3). Такие фигуры можно понимать как вырожденные тела (отсюда и название диэдрон (dihedron').
Примеры симметрии двумерных диэдралов
-
D5 – Красная звезда.
-
D8 – Руб аль-хизб.
-
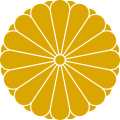
D16 – Императорская печать Японии.
-
D24 – Ашока Чакра - символ на флаге Индии.
Эквивалентные определения
Следующие определения [math]\displaystyle{ \mathrm{Dih}_n }[/math] эквивалентны:
- Группа автоморфизмов графа состоящего только из цикла с [math]\displaystyle{ n }[/math] вершинами (если [math]\displaystyle{ n\geqslant 3 }[/math]).
- Группа с представлением
- [math]\displaystyle{ D_{n}=\langle r, s \mid r^n = 1, s^2 = 1, srs = r^{-1} \rangle }[/math]
- или
- [math]\displaystyle{ D_n=\langle x, y \mid x^n = y^2 = (xy)^2 = 1 \rangle. }[/math]
- Из второго представления следует, что [math]\displaystyle{ \mathrm{Dih}_n }[/math] принадлежит к классу групп Коксетера.
Свойства
Свойства диэдральных групп [math]\displaystyle{ \mathrm{Dih}_n }[/math] с [math]\displaystyle{ n\geqslant 3 }[/math] зависят от чётности [math]\displaystyle{ n }[/math]. Например, центр группы [math]\displaystyle{ \mathrm{Dih}_n }[/math] состоит только из тождества при нечётном [math]\displaystyle{ n }[/math] и из двух элементов при чётном, а именно, из тождества и [math]\displaystyle{ r^{n/2} }[/math]. Для нечётных [math]\displaystyle{ n }[/math] абстрактная группа [math]\displaystyle{ \mathrm{Dih}_{2n} }[/math] изоморфна прямому произведению [math]\displaystyle{ \mathrm{Dih}_n }[/math] и [math]\displaystyle{ \mathrm{Z}_2 }[/math].
Если [math]\displaystyle{ m }[/math] делит [math]\displaystyle{ n }[/math], то [math]\displaystyle{ \mathrm{Dih}_n }[/math] имеет [math]\displaystyle{ n/m }[/math] подгрупп вида [math]\displaystyle{ \mathrm{Dih}_m }[/math] и одну подгруппу [math]\displaystyle{ \mathrm{Z}_m }[/math]. Таким образом, полное число подгрупп группы [math]\displaystyle{ \mathrm{Dih}_n }[/math] ([math]\displaystyle{ n\geqslant 1 }[/math]), равно [math]\displaystyle{ \mathrm{d}(n)+\mathrm{\sigma}(n) }[/math], где [math]\displaystyle{ \mathrm{d}(n) }[/math] — число натуральных делителей [math]\displaystyle{ n }[/math] и [math]\displaystyle{ \mathrm{\sigma}(n) }[/math] — сумма натуральных делителей [math]\displaystyle{ n }[/math].
Сопряжённость классов отражений
Все отражения попарно сопряжены в случае нечётного [math]\displaystyle{ n }[/math], но распадаются на два класса сопряжённости при чётном [math]\displaystyle{ n }[/math]. В терминах изоморфизма правильных [math]\displaystyle{ n }[/math]-угольников: для нечётных [math]\displaystyle{ n }[/math] любое отражение получается из любого другого применением поворота, в то время как для чётных [math]\displaystyle{ n }[/math] только половина отражений может быть получена из некоторого отражения поворотами. С геометрической точки зрения, в нечётноугольнике каждая ось симметрии проходит через одну из вершин и середину противоположной стороны, а в чётноугольнике имеется два набора осей, каждый набор соответствует своему классу сопряжённости — оси, проходящие через вершины и оси, проходящие через середины сторон.
Алгебраически это представители сопряжённых элементов из теоремы Силова: для нечётных [math]\displaystyle{ n }[/math] любое отражение вместе с тождественным элементом образует подгруппу порядка [math]\displaystyle{ 2 }[/math], являющуюся силовской 2-подгруппой ([math]\displaystyle{ 2=2^1 }[/math] — максимальная степень двойки, делящая [math]\displaystyle{ 2n=2(2k+1) }[/math]), в то время как для чётных [math]\displaystyle{ n }[/math], эти подгруппы [math]\displaystyle{ 2 }[/math]-го порядка не являются силовскими, поскольку [math]\displaystyle{ 4 }[/math] (наибольшая степень двойки) делит порядок группы.
Для чётного [math]\displaystyle{ n }[/math] вместо этого имеется внешний автоморфизм, переставляющий два типа отражений.
Группы автоморфизмов
Автоморфизм группы Dihn изоморфен аффинной группе Aff(Z/nZ) [math]\displaystyle{ =\{ax + b \mid (a,n) = 1\} }[/math] и имеет порядок [math]\displaystyle{ n\phi(n), }[/math], где [math]\displaystyle{ \phi }[/math] — функция Эйлера, равная количеству натуральных чисел, меньших n и взаимно простых с ним.
Это можно понять в терминах генератора отражений и элементарных вращений (вращений на [math]\displaystyle{ k(2\pi/n) }[/math], для k взаимно-простого с n). Какой автоморфизм будет внутренним, а какой внешним, зависит от чётности n.
- Для нечётного n диэдральная группа не имеет центра, так что любой элемент определяет нетривиальный внутренний автоморфизм. Для чётного n вращение на 180° (отражение относительно центра координат) является нетривиальным элементом центра.
- Таким образом, для нечётного n, внутренняя группа автоморфизма имеет порядок 2n, а для чётного — порядок n.
- Для нечётного n, все отражения являются сопряжёнными, для чётного, они распадаются на два класса (те, которые проходят через две вершины, и те, которые проходят через середины сторон), и эти два класса связаны с внешним автоморфизмом, который можно представить как вращение на [math]\displaystyle{ \pi/n }[/math] (половину угла минимального вращения).
- Вращения дают нормальную подгруппу. Сопряжение отражения меняет знак (направление) вращения, но в остальном их не меняют. Автоморфизм, умножающий углы на k (взамнопростое с n) является внешним, если только не [math]\displaystyle{ k=\pm 1. }[/math]
Примеры автоморфизма групп
Dih9 имеет 18 внутренних автоморфизмов. Как группа изометрий двумерного пространства, D9 имеет отражения с интервалом 20°. 18 внутренних автоморфизмов обеспечивают вращения отражений на число, кратное 20°, и отражения. Как группы изометрии они все являются аутоморфизмами. Имеется ещё, вдобавок, 36 внешних автоморфизмов, например, умножая угол вращения на 2.
Обобщения
Имеется несколько важных обобщений диэдральных групп:
- Бесконечная диэдральная группа — это бесконечная группа с алгебраической структурой, похожей на структуру конечных диэдральных групп. Её можно рассматривать как группу симметрий целых чисел.
- Ортогональная группа O(2), то есть группа симметрии круга, имеет свойства, похожие на свойства конечных диэдральных групп
- Семейство обобщенных диэдральных групп включает вышеприведенные расширения, как и многие другие.
- Квазиэдральные группы — это семейство конечных групп со свойствами, похожими на свойства конечных диэдральных групп.
См. также
Примечания
- ↑ Dummit, David S.; Foote, Richard M. Abstract Algebra (неопр.). — 3rd. — John Wiley & Sons, 2004. — ISBN 0-471-43334-9.
Ссылки
- Dihedral Group n of Order 2n by Shawn Dudzik, Wolfram Demonstrations Project.
- Dihedral group at Groupprops
- Miller W., Symmetry Groups and Their Applications. Academic Press, 1972.
- Узоры симметрии = Patterns of Symmetry / Под ред. М. Сенешаль, Дж. Флека. — М.: Мир, 1980. — 271 с.
- Аминов Л. К. Теория симметрии (конспекты лекций и задачи). — М.: Мн-т компьютерных исследований, 2002. — 192 с.
- Вейль Г. Симметрия = Symmetry. — М.: Наука, 1968. — 152 с.
- Вигнер Е. Этюды о симметрии = Symmetries and Reflections: Scientific Essays. — М.: Мир, 1971. — 320 с.
- Голод П. И., Климык А. У. Математические основ теории симметрий = Математичні основи теорії симетрій. — Ижевск: РХД, 2001. — 528 с.
- Поклонский Н. А. Точечные группы симметрии: Учеб. Пособие — Мн.: БГУ, 2003. — ISBN 985-445-965-9
- Смирнов Е. Ю. Группы отражений и правильные многогранники. — М.: МЦНМО, 2009. — 48 с. — ISBN 978-5-94057-525-2
- Фларри Р. Группы симметрии: Теория и химические приложения = Symmetry Groups: Theory and Chemical Applications. — М.: Мир, 1983. — 400 с.
Для улучшения этой статьи по математике желательно: |