Хроматический многочлен

Все неизоморфные графы с 3 вершинами и их хроматические многочлены, по часовой стрелке сверху.
Независимое 3-множество: [math]\displaystyle{ k^3 }[/math].
Ребро и одна вершина: [math]\displaystyle{ k^2(k-1) }[/math].
3-путь: [math]\displaystyle{ k(k-1)^2 }[/math].
3-клика: [math]\displaystyle{ k(k-1)(k-2) }[/math].

Хроматический многочлен — многочлен, изучаемый в алгебраической теории графов, представляющий число раскрасок графа как функцию от числа цветов. Первоначально определён Джорджем Биркгофов для попытки решения на проблемы четырёх красок. Обобщен и систематически изучен Хасслером Уитни, Татт обобщил хроматический многочлен до многочлена Татта, связав его с моделью Поттса статистической физики.

История

Джордж Биркгоф ввёл хроматический многочлен в 1912 году, определяя его только для планарных графов в попытке доказать теорему о четырёх красках. Если [math]\displaystyle{ P(G, k) }[/math] обозначает число правильных раскрасок графа G k цветами, то можно было бы доказать теорему о четырёх красках, показав, что [math]\displaystyle{ P(G, 4)\gt 0 }[/math] для всех планарных графов G. Таким образом он надеялся использовать мощь математического анализа и алгебры для изучения корней многочленов для изучения комбинаторной задачи раскраски.

Хасслер Уитни обобщил многочлен Биркгофа с планарного случая на графы общего вида в 1932. В 1968 году Рид поднял вопрос: какие многочлены являются хроматическими многочленами для некоторых графов (задача остаётся открытой), и ввёл понятие хроматически эквивалентных графов. В настоящее время хроматические многочлены являются центральными объектами алгебраической теории графов.

Определение

Все правильные раскраски графов с 3 вершинами при использовании kцветов ([math]\displaystyle{ k=0,1,2,3 }[/math]). Хроматический многочлен каждого графа интерполирует число правильных раскрасок.

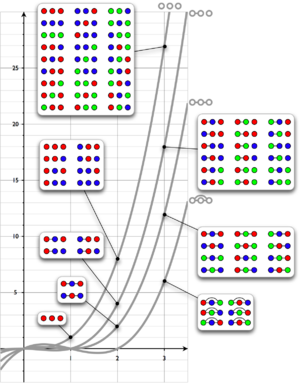
Хроматический многочлен графа G считает число правильных раскрасок вершин. Обычно многочлен обозначается как [math]\displaystyle{ P_G(k) }[/math], [math]\displaystyle{ \chi_G(k) }[/math], [math]\displaystyle{ \pi_G(k) }[/math] или [math]\displaystyle{ P(G, k) }[/math]. Последнее обозначение будем использовать в остальной части статьи.

Например, путь [math]\displaystyle{ P_3 }[/math] с 3 вершинами не может быть раскрашен в 0 цветов или 1 цветом. Используя 2 цвета граф можно раскрасить двумя способами. Используя 3 цвета граф можно раскрасить 12 способами.

Доступно цветов [math]\displaystyle{ k }[/math]	0	1	2	3
Число раскрасок [math]\displaystyle{ P(P_3, k) }[/math]	0	0	2	12

Для графа G с n вершинами хроматический многочлен определяется как уникальный интерполирующий многочлен степени, не превосходящей n, проходящий через точки

[math]\displaystyle{ \left \{ (0, P(G, 0)), (1, P(G, 1)), \cdots, (n, P(G, n)) \right \}. }[/math]

Если граф G не содержит вершин с петлями, то хроматический многочлен является приведённым многочленом степени в точности n. Фактически, для приведённого выше примера мы имеем

[math]\displaystyle{ P(P_3, t)= t(t-1)^2, \qquad P(P_3, 3)=12. }[/math]

Хроматический многочлен включает по меньшей мере столько информации о раскрашиваемости графа G, сколько содержится в хроматическом числе. Более того, хроматическое число является наименьшим положительным целым, при котором хроматический многочлен не обращается в нуль,

[math]\displaystyle{ \chi (G)=\min\{ k : P(G, k) \gt 0 \}. }[/math]

Примеры

Хроматические многочлены для некоторых графов

Треугольник [math]\displaystyle{ K_3 }[/math]	[math]\displaystyle{ t(t-1)(t-2) }[/math]
Полный граф [math]\displaystyle{ K_n }[/math]	[math]\displaystyle{ t(t-1)(t-2)\cdots(t-(n-1)) }[/math]
Путь [math]\displaystyle{ P_n }[/math]	[math]\displaystyle{ t(t-1)^{n-1} }[/math]
Любое дерево с n вершинами	[math]\displaystyle{ t(t-1)^{n-1} }[/math]
Цикл [math]\displaystyle{ C_n }[/math]	[math]\displaystyle{ (t-1)^n+(-1)^n(t-1) }[/math]
Граф Петерсена	[math]\displaystyle{ t(t-1)(t-2) \left (t^7-12t^6+67t^5-230t^4+529t^3-814t^2+775t-352 \right) }[/math]

Свойства

Для фиксированного графа G с n вершинами хроматический многочлен [math]\displaystyle{ P(G, t) }[/math] является, фактически, многочленом степени n. По определению, вычисление значения многочлена [math]\displaystyle{ P(G, k) }[/math] даёт число k-раскрасок графа G для [math]\displaystyle{ k=0, 1,\cdots, n }[/math]. То же самое верно для k > n.

Выражение

[math]\displaystyle{ (-1)^{|V(G)|} P(G,-1) }[/math]

даёт число ациклических ориентаций графа G.

Значение производной от многочлена в точке 1, [math]\displaystyle{ P'(G, 1) }[/math] равно с точностью до знака хроматическому инварианту [math]\displaystyle{ \theta(G) }[/math].

Если граф G имеет n вершин, m рёбер и c компонент [math]\displaystyle{ G_1, \cdots, G_c }[/math], то

• Коэффициенты при [math]\displaystyle{ t^0, \cdots, t^{c-1} }[/math] равны нулю.
• Коэффициенты при [math]\displaystyle{ t^c, \cdots, t^n }[/math] все ненулевые.
• Коэффициент при [math]\displaystyle{ t^n }[/math] в [math]\displaystyle{ P(G, t) }[/math] равен 1.
• Коэффициент при [math]\displaystyle{ t^{n-1} }[/math] в [math]\displaystyle{ P(G, t) }[/math] равен [math]\displaystyle{ -m }[/math].
• Коэффициенты любого хроматического многочлена знакопеременны.
• Абсолютные значения коэффициентов любого хроматического многочлена образует логарифмически вогнутую последовательность.
• [math]\displaystyle{ P(G, t) = P(G_1, t)P(G_2,t) \cdots P(G_c,t) }[/math]

Граф G с n вершинами является деревом тогда и только тогда, когда

[math]\displaystyle{ P(G, t) = t(t-1)^{n-1}. }[/math]

Хроматическая эквивалентность

Три графа с хроматическим многочленом, равным [math]\displaystyle{ (x-2)(x-1)^3x }[/math].

Говорят, что два графа хроматически эквивалентны, если они имеют одинаковые хроматические многочлены. Изоморфные графы имеют одинаковые хроматические многочлены, но неизоморфные графы могут быть хроматически эквивалентными. Например, все деревья с n вершинами имеют одинаковые хроматические многочлены:

[math]\displaystyle{ (x-1)^{n-1}x, }[/math]

В частности,

[math]\displaystyle{ (x-1)^3x }[/math]

является хроматическим многочленом как для клешни, так и для пути с 4 вершинами.

Хроматическая единственность

Граф является хроматически уникальным, если он определяется хроматическим многочленом с точностью до изоморфизма. Другими словами, если граф G хроматически уникален, то из [math]\displaystyle{ P(G, t) = P(H, t) }[/math] следует, что G и H изоморфны.

Все циклы хроматически уникальны.

Хроматические корни

Корень (или нуль) хроматического многочлена (называется «хроматическим корнем») — это значение x, для которого [math]\displaystyle{ P(G, x)=0 }[/math]. Хроматические корни хорошо изучены. Фактически, исходным побуждением Биркгофа для введения хроматического многочлена было показать, что для планарных графов [math]\displaystyle{ P(G, x)\gt 0 }[/math] для x ≥ 4. Это доказало бы теорему о четырёх красках.

Никакой граф нельзя раскрасить в 0 цветов, так что 0 всегда является хроматическим корнем. Только графы без рёбер могут быть раскрашены в один цвет, так что 1 является хроматическим корнем любого графа, имеющего по меньшей мере одно ребро. С другой стороны, за исключением этих двух случаев, никакой граф не может иметь в качестве хроматического корня вещественное число, меньшее либо равное 32/27. Результат Татта связывает золотое сечение [math]\displaystyle{ \phi }[/math] с изучением хроматических корней, показывая, что хроматические корни существуют очень близко к [math]\displaystyle{ \phi^2 }[/math] — если [math]\displaystyle{ G_n }[/math] является планарной триангуляцией сферы, то

[math]\displaystyle{ P(G_n,\phi^2) \leq \phi^{5-n}. }[/math]

В то время как вещественная прямая, таким образом, имеет большие куски, которые не содержат хроматических корней ни для какого графа, любая точка на комплексной плоскости произвольно близка к хроматическому корню в том смысле, что существует бесконечное семейство графов, хроматические корни которых плотны на комплексной плоскости.

Категоризация

Хроматический многочлен категоризирован с помощью теории гомологий, близко связанной с гомологией Хованова.

Алгоритмы

Хроматический многочлен
Вход	Граф G с n вершинами.
Выход	Коэффициенты [math]\displaystyle{ P(G, t) }[/math]
Время работы	[math]\displaystyle{ O(2^nn^r) }[/math] для некоторой константы [math]\displaystyle{ r }[/math]
Сложность	#P-трудна
Сводится из	#3SAT

#k-раскраски
Вход	Граф G с n вершинами.
Выход	[math]\displaystyle{ P(G, k) }[/math]
Время работы	Принадлежит P для [math]\displaystyle{ k=0,1,2 }[/math]. [math]\displaystyle{ O(1{,}6262^n) }[/math] для [math]\displaystyle{ k=3 }[/math]. В противном случае [math]\displaystyle{ O(2^nn^r) }[/math] для некоторой константы [math]\displaystyle{ r }[/math]
Сложность	#P-трудна пока [math]\displaystyle{ k=0,1,2 }[/math]
Approximability	No FPRAS for [math]\displaystyle{ k\gt 2 }[/math]

Вычислительные задачи, связанные с хроматическими многочленами

• нахождение хроматического многочлена [math]\displaystyle{ P(G, t) }[/math] для данного графа G;
• вычисление [math]\displaystyle{ P(G, k) }[/math] в фиксированной точке k для данного графа G.

Первая задача более общая, поскольку, зная коэффициенты [math]\displaystyle{ P(G, t) }[/math], мы можем вычислить значение многочлена в любой точке за полиномиальное время. Вычислительная сложность второй задачи сильно зависит от величины k. Когда k является натуральным числом, задачу можно рассматривать как вычисление количества k-раскрасок данного графа. Например, задача включает подсчёт 3-раскрасок в качестве канонической задачи для изучения сложности подсчёта. Эта задача является полной в классе #P.

Эффективные алгоритмы

Для некоторых базовых классов графов известны явные формулы хроматических многочленов. Например, это верно для деревьев и клик, что показано в таблице выше.

Известны алгоритмы полиномиального времени для вычисления хроматического многочлена для широкого класса графов, в который входят хордальные графы и графы с ограниченной кликовой шириной. Второй из этих классов, в свою очередь, включает кографы и графы с ограниченной древесной шириной, такие как внешнепланарные графы.

В интернете присутствуют лица, пытающиеся решить задачу коллективно, и им помогают активные автономные помощники, особенно для хроматических многочленов высокой степени.

Удаление — стягивание

Рекурсивный способ вычисления хроматического многочлена базируется на стягивании ребра — для пары вершин [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] граф [math]\displaystyle{ G/uv }[/math] получается путём слияния двух вершин и удаления ребра между ними. Хроматический многочлен удовлетворяет рекурсивному соотношению

[math]\displaystyle{ P(G,k)=P(G-uv, k)- P(G/uv,k) }[/math],

где [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] являются смежными вершинами и [math]\displaystyle{ G-uv }[/math] является графом с удалённым ребром [math]\displaystyle{ uv }[/math]. Эквивалентно,

[math]\displaystyle{ P(G,k)= P(G+uv, k) + P(G/uv,k) }[/math]

если [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] не смежны и [math]\displaystyle{ G+uv }[/math] является графом с добавленным ребром [math]\displaystyle{ uv }[/math]. В первой форме рекурсия прекращается на наборе пустых графов. Эти рекуррентные отношения называются также фундаментальной теоремой редукции. Вопрос Татта о том, какие другие свойства графа удовлетворяют тем же рекуррентным соотношениям, привёл к открытию обобщения хроматического многочлена на две переменные — многочлену Татта.

Выражения дают рекурсивную процедуру, называемую алгоритмом удаления — стягивания, которая является базисом многих алгоритмов раскраски графов. Функция ChromaticPolynomial в системе компьютерной алгебры Mathematica использует вторую рекуррентную формулу если граф плотный, и первую, если граф разреженный. Худшее время работы для обоих формул удовлетворяет рекуррентному соотношению для чисел Фибоначчи, так что в худшем случае алгоритм работает за время (с точностью до некоторого полиномиального коэффициента)

[math]\displaystyle{ \phi^{n+m}=\left (\frac{1+\sqrt{5}}{2} \right)^{n+m}\in O\left(1{,}62^{n+m}\right) }[/math]

на графе с n вершинами и m рёбрами. Анализ времени работы можно улучшить до полиномиального множителя числа [math]\displaystyle{ t(G) }[/math] остовных деревьев входного графа. На практике используется стратегия ветвей и границ вместе с отбрасыванием изоморфных графов, чтобы исключить рекурсивные вызовы, и время зависит от эвристики, используемой при выборе пары вершин (для исключения-стягивания).

Метод куба

Существует естественный геометрический подход к раскраске графов, если заметить, что при назначении натуральных чисел каждой вершине раскраска графов является вектором целочисленной решётки. Поскольку присвоение двум вершинам [math]\displaystyle{ i }[/math] и [math]\displaystyle{ j }[/math] одного цвета эквивалентно равенству координат [math]\displaystyle{ i }[/math] и [math]\displaystyle{ j }[/math] в векторе раскраски, каждое ребро можно ассоциировать с гиперплоскостью вида [math]\displaystyle{ \{x\in R^d:x_i=x_j\} }[/math]. Набор таких гиперплоскостей для данного графа называется его графической конфигурацией гиперплоскостей. Правильная раскраска графа — это раскраска, вектор которой не оказывается на запрещённой плоскости. Ограниченные множеством цветов [math]\displaystyle{ k }[/math], точки решётки попадают в куб [math]\displaystyle{ [0,k]^n }[/math]. В этом контексте хроматический многочлен подсчитывает точки решётки в [math]\displaystyle{ [0,k] }[/math]-кубе, которые не попадают на графическую конфигурацию.

Вычислительная сложность

Задача вычисления числа 3-раскрасок данного графа является каноническим примером #P-полной задачи, так что задача вычисления коэффициентов хроматического многочлена #P-трудна. Аналогично, вычисление [math]\displaystyle{ P(G, 3) }[/math] для данного графа G #P-полна. С другой стороны, для [math]\displaystyle{ k=0,1,2 }[/math] легко вычислить [math]\displaystyle{ P(G, k) }[/math], так что соответствующие задачи имеют полиномиальную по времени трудность. Для целых чисел [math]\displaystyle{ k\gt 3 }[/math] задача #P-трудна, что устанавливается подобно случаю [math]\displaystyle{ k=3 }[/math]. Фактически, известно, что [math]\displaystyle{ P(G, x) }[/math] #P-трудна для всех x (включая отрицательные целые числа и даже все комплексные числа), за исключением трёх «простых точек». Таким образом, сложность вычисления хроматического многочлена полностью понятна.

В многочлене

[math]\displaystyle{ P(G, t)= a_1 t + a_2t^2+\dots +a_nt^n, }[/math]

коэффициент [math]\displaystyle{ a_n }[/math] всегда равен 1, а также известны некоторые другие свойства коэффициентов. Это поднимает вопрос, нельзя ли вычислить некоторые коэффициенты попроще. Однако задача вычисления a_r для фиксированного r и данного графа G является #P-трудной.

Не известно никакого аппроксимационного алгоритма вычисления [math]\displaystyle{ P(G, x) }[/math] для любого x, за исключением трёх простых точек. В целых точках [math]\displaystyle{ k=3,4,\dots }[/math] соответствующая задача разрешимости определения, может ли данный граф быть раскрашен в k цветов, NP-трудна. Такие задачи не могут быть аппроскимированы с любым коэффициентом с помощью полиномиального вероятностного алгоритма с ограниченной ошибкой, разве только NP = RP, поскольку любая мультипликативная аппроксимация различала бы значения 0 и 1, что было бы эффективным решением задачи с помощью полиномиального вероятностного алгоритма с ограниченной ошибкой в форме задачи разрешимости. В частности, при некоторых предположениях, это исключает возможность полностью полиномиальной рандомизированной аппроксимационной схемы (FPRAS). Для других точек нужны более сложные рассуждения и вопрос находится в фокусе активных поисков. На 2008 известно, что не существует FPRAS-схемы для вычиcления [math]\displaystyle{ P(G, x) }[/math] для любого x > 2, разве только NP = RP.

Литература

• А. Ю. Эвнин. Хроматический многочлен графа в задачах (рус.) // Математическое образование. — 2014. — № 4(72). — С. 9—15.
• Biggs N. Algebraic Graph Theory. — Cambridge University Press, 1993. — ISBN 0-521-45897-8.
• Hirokazu Shirado, Nicholas A. Christakis. Locally noisy autonomous agents improve global human coordination in network experiments // Nature. — 2017. — Т. 545, вып. 7654. — С. 370–374. — doi:10.1038/nature22332.
• Chao C.-Y., Whitehead E. G. On chromatic equivalence of graphs // Theory and Applications of Graphs. — Springer, 1978. — Т. 642. — С. 121–131. — (Lecture Notes in Mathematics). — ISBN 978-3-540-08666-6.
• Dong F. M., Koh K. M., Teo K. L. Chromatic polynomials and chromaticity of graphs. — World Scientific Publishing Company, 2005. — ISBN 981-256-317-2.
• Giménez O., Hliněný P., Noy M. Computing the Tutte polynomial on graphs of bounded clique-width // Proc. 31st Int. Worksh. Graph-Theoretic Concepts in Computer Science (WG 2005). — Springer-Verlag, 2005. — Т. 3787. — С. 59–68. — doi:10.1007/11604686_6.
• Goldberg L.A., Jerrum M. Inapproximability of the Tutte polynomial // Information and Computation. — 2008. — Т. 206, вып. 7. — С. 908. — doi:10.1016/j.ic.2008.04.003.
• Laure Helme-Guizon, Yongwu Rong. A categorification of the chromatic polynomial // Algebraic & Geometric Topology. — 2005. — Т. 5, вып. 4. — С. 1365–1388. — doi:10.2140/agt.2005.5.1365.
• Huh J. Milnor numbers of projective hypersurfaces and the chromatic polynomial of graphs. — arXiv:1008.4749v3, 2012.
• Jackson B. A Zero-Free Interval for Chromatic Polynomials of Graphs // Combinatorics, Probability and Computing. — 1993. — Т. 2. — С. 325–336. — doi:10.1017/S0963548300000705.
• Jaeger F., Vertigan D. L., Welsh D. J. A. On the computational complexity of the Jones and Tutte polynomials // Mathematical Proceedings of the Cambridge Philosophical Society. — 1990. — Т. 108. — С. 35–53. — doi:10.1017/S0305004100068936.
• Linial N. Hard enumeration problems in geometry and combinatorics // SIAM J. Algebraic Discrete Methods. — 1986. — Т. 7, вып. 2. — С. 331–335. — doi:10.1137/0607036.
• Makowsky J. A., Rotics U., Averbouch I., Godlin B. Computing graph polynomials on graphs of bounded clique-width // Proc. 32nd Int. Worksh. Graph-Theoretic Concepts in Computer Science (WG 2006). — Springer-Verlag, 2006. — Т. 4271. — С. 191–204. — (Lecture Notes in Computer Science). — doi:10.1007/11917496_18.
• Naor J., Naor M., Schaffer A. Fast parallel algorithms for chordal graphs // Proc. 19th ACM Symp. Theory of Computing (STOC '87). — 1987. — С. 355–364. — doi:10.1145/28395.28433.
• Oxley J. G., Welsh D. J. A. Chromatic, flow and reliability polynomials: The complexity of their coefficients. // Combinatorics, Probability and Computing. — 2002. — Т. 11, вып. 4. — С. 403–426.
• Pemmaraju S., Skiena S. section 7.4.2 // Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. — Cambridge University Press, 2003. — ISBN 0-521-80686-0.
• Sekine K., Imai H., Tani S. Computing the Tutte polynomial of a graph of moderate size // Algorithms and Computation, 6th International Symposium, Lecture Notes in Computer Science 1004. — Cairns, Australia, December 4–6, 1995: Springer, 1995. — С. 224–233.
• Sokal A. D. Chromatic Roots are Dense in the Whole Complex Plane // Combinatorics, Probability and Computing. — 2004. — Т. 13, вып. 2. — С. 221–261. — doi:10.1017/S0963548303006023.
• Stanley R. P. Acyclic orientations of graphs // Disc. Math.. — 1973. — Т. 5, вып. 2. — С. 171–178. — doi:10.1016/0012-365X(73)90108-8.
• Vitaly I. Voloshin. Coloring Mixed Hypergraphs: Theory, Algorithms and Applications.. — American Mathematical Society, 2002. — ISBN 0-8218-2812-6.
• Wilf H. S. Algorithms and Complexity. — Prentice–Hall, 1986. — ISBN 0-13-021973-8.

Ссылки

• Weisstein, Eric W. Chromatic polynomial (англ.) на сайте Wolfram MathWorld.
• PlanetMath Chromatic polynomial
• Code for computing Tutte, Chromatic and Flow Polynomials by Gary Haggard, David J. Pearce and Gordon Royle: [1] (недоступная ссылка)