Раскраска графов

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
Корректная раскраска вершин графа наименьшим набором цветов — тремя.

Раскраска графа — теоретико-графовая конструкция, частный случай разметки графа. При раскраске элементам графа ставятся в соответствие метки с учётом определённых ограничений; эти метки традиционно называются «цветами». В простейшем случае такой способ окраски вершин графа, при котором любым двум смежным вершинам соответствуют разные цвета, называется раскраской вершин. Аналогично раскраска рёбер присваивает цвет каждому ребру так, чтобы любые два смежных ребра имели разные цвета[1]. Наконец, раскраска областей планарного графа назначает цвет каждой области, так, что каждые две области, имеющие общую границу, не могут иметь одинаковый цвет.

Раскраска вершин — главная задача раскраски графов, все остальные задачи в этой области могут быть сведены к ней. Например, раскраска рёбер графа — это раскраска вершин его рёберного графа, а раскраска областей планарного графа — это раскраска вершин его двойственного графа[1]. Тем не менее, другие проблемы раскраски графов часто ставятся и решаются в изначальной постановке. Причина этого частично заключается в том, что это даёт лучшее представление о происходящем и более показательно, а частично из-за того, что некоторые задачи таким образом решать удобнее (например, раскраска рёбер).

Раскраска графов находит применение и во многих практических областях, а не только в теоретических задачах. Помимо классических типов проблем, различные ограничения могут также быть наложены на граф, на способ присвоения цветов или на сами цвета. Этот метод, например, используется в популярной головоломке Судоку. В этой области всё ещё ведутся активные исследования.

История

Первые результаты были получены для плоских графов в задаче раскрашивания карт. Пытаясь раскрасить карту округов Англии, Францис Гутри[англ.] сформулировал проблему четырёх красок, отметив, что четырёх цветов достаточно, чтобы раскрасить карту так, чтобы любые два смежных региона имели разные цвета. Его брат передал вопрос своему учителю по математике, Огастесу де Моргану, который упомянул о нём в своем письме Уильяму Гамильтону в 1852 году. Артур Кэли поднял эту проблему на встрече Лондонского математического сообщества в 1878 году. В том же году Тэйтом было предложено первое решение этой задачи. Раскраску вершин первоначального графа он свел к раскраске рёбер двойственного графа и предположил, что эта задача всегда имеет решение[2]. В 1880 году Альфред Кемпе[англ.] опубликовал статью, в которой утверждалось, что ему удалось установить результат, и на десятилетие проблема четырёх цветов считалась решённой. За это достижение Кемпе был избран членом Лондонского Королевского общества и позже — президентом Лондонского математического сообщества[3].

В 1890 году Хивуд нашёл ошибку в доказательстве Кемпе. В этой же статье он доказал теорему пяти красок[англ.], показав, что любая плоская карта может быть раскрашена не более, чем пятью цветами. При этом он опирался на идеи Кемпе. В следующем столетии было разработано большое количество теорий в попытках уменьшить минимальное число цветов. Теорема четырёх красок была окончательно доказана в 1977 году учеными Кеннетом Аппелем[англ.] и Вольфгангом Хакеном с использованием компьютерного перебора. Идея доказательства во многом опиралась на идеи Хивуда и Кемпе и игнорировала большинство промежуточных исследований[4]. Доказательство теоремы четырёх красок является одним из первых доказательств, в которых был использован компьютер.

В 1912 году Джордж Дэвид Биркхоф предложил использовать для изучения задач раскраски хроматический многочлен, являющийся важной частью в алгебраической теории графов. Хроматический многочлен впоследствии был обобщён Уильямом Таттом (многочлен Татта). Кемпе в 1879 году уже обращал внимание на общий случай, когда граф не являлся плоским[5]. Много результатов обобщений раскраски плоских графов на поверхности более высоких порядков появилось в начале XX века.

В 1960 году Клод Бердж[англ.] сформулировал гипотезу о совершенных графах, мотивированное понятием из теории информации, а именно нулевой ошибкой ёмкости графа[6], представленным Шенноном. Утверждение оставалось неподтвержденным на протяжении 40 лет, пока не было доказано как знаменитая строгая теорема о совершенных графах математиками Чудновской[англ.], Робертсоном[англ.], Сеймуром и Томасом в 2002 году.

Раскраска графов как алгоритмическая проблема начала изучаться с 1970-х годов: определение хроматического числа — входит в число 21 NP-полных задач Карпа (1972). И примерно в то же время были разработаны разнообразные алгоритмы на базе поиска с возвратом и рекурсивного удаления и стягивания Зыкова[7]. С 1981 года раскраска графа применяется для распределения регистров в компиляторах[8].

Определение и терминология

Раскраска вершин

Этот граф может быть раскрашен 3 цветами 12 способами.

Когда говорят о раскраске графов, почти всегда подразумевают под этим раскраску их вершин, то есть присвоение цветовых меток вершинам графа так, чтобы любые две вершины, имеющие общее ребро, имели разные цвета. Так как графы, в которых есть петли, не могут быть раскрашены таким образом, они не являются предметом обсуждения.

Терминология, в которой метки называются цветами, происходит от раскраски политических карт. Такие метки как красный или синий используются, только когда число цветов мало, обычно же подразумевается, что метки являются целыми числами [math]\displaystyle{ \{1,2,3,...\} }[/math].

Раскраска с использованием [math]\displaystyle{ k }[/math] цветов называется [math]\displaystyle{ k }[/math]-раскраской. Наименьшее число цветов, необходимое для раскраски графа [math]\displaystyle{ G }[/math], называется его хроматическим числом и часто записывается как [math]\displaystyle{ \chi(G) }[/math]. Иногда используется [math]\displaystyle{ \gamma(G) }[/math], с тех пор как [math]\displaystyle{ \chi(G) }[/math] обозначает Эйлерову характеристику. Подмножество вершин, выделенных одним цветом, называется цветовым классом, каждый такой класс формирует независимый набор. Таким образом, [math]\displaystyle{ k }[/math]-раскраска — это то же самое, что и разделение вершин на [math]\displaystyle{ k }[/math] независимых наборов[1].

Хроматическое число в терминах расстояния Громова-Хаусдорфа

Пусть [math]\displaystyle{ G }[/math] — произвольный граф с множеством вершин [math]\displaystyle{ V }[/math]. Фиксируем два положительных вещественных числа [math]\displaystyle{ a\lt b\le 2a }[/math], и будем рассматривать [math]\displaystyle{ V }[/math] как метрическое пространство, в котором расстояния между смежными вершинами равны [math]\displaystyle{ b }[/math], в все остальные ненулевые расстояния равны [math]\displaystyle{ a }[/math]. Обозначим через [math]\displaystyle{ a\Delta_m }[/math] метрическое пространство, состоящее из [math]\displaystyle{ m }[/math] точек, удаленных друг от друга на расстояние [math]\displaystyle{ a }[/math]. Наконец, для любых двух метрических пространств [math]\displaystyle{ X }[/math] и [math]\displaystyle{ Y }[/math], через [math]\displaystyle{ d_{GH}(X,Y) }[/math] обозначим расстояние Громова-Хаусдорфа между [math]\displaystyle{ X }[/math] и [math]\displaystyle{ Y }[/math]. Тогда имеет место следующий результат.

Теорема (А.О.Иванов, А.А.Тужилин)[9]: Пусть [math]\displaystyle{ m }[/math] — наибольшее натуральное число, для которого [math]\displaystyle{ d_{GH}(V,a\Delta_m)=b }[/math] (если таких натуральных чисел не существует, то положим [math]\displaystyle{ m=0 }[/math]). Тогда [math]\displaystyle{ \chi(G)=m+1 }[/math].

Замечание.

  • Хроматическое число [math]\displaystyle{ \chi(G) }[/math] равно [math]\displaystyle{ 1 }[/math], если и только если граф [math]\displaystyle{ G }[/math] не содержит ни одного ребра. В этом случае равенство [math]\displaystyle{ d_{GH}(V,a\Delta_m)=b }[/math] не выполняется ни для какого [math]\displaystyle{ m }[/math], поэтому, в силу сделанного соглашения, [math]\displaystyle{ m=0 }[/math], что приводит к верному равенству [math]\displaystyle{ \chi(G)=0+1=1 }[/math].
  • По определению, [math]\displaystyle{ \chi(G) }[/math] не превосходит количества [math]\displaystyle{ n }[/math] элементов множества [math]\displaystyle{ V }[/math]. С другой стороны, несложно показать, что [math]\displaystyle{ d_{GH}(V,a\Delta_p)\le\max\{a,\,b-a\}\lt b }[/math] при каждом [math]\displaystyle{ p\ge n }[/math], поэтому [math]\displaystyle{ m\lt n }[/math] и, значит, [math]\displaystyle{ \chi(G)=m+1\le n }[/math].

Хроматический многочлен

Основная статья: Хроматическое число § Хроматический многочлен

Хроматический многочлен — это функция [math]\displaystyle{ P(G,t) }[/math], которая считает число t-раскрасок графа [math]\displaystyle{ G }[/math]. Из названия следует, что для заданных [math]\displaystyle{ G }[/math] эта функция является многочленом, зависящим от t.

Этот факт был обнаружен Биркгофом и Льюисом при попытке доказать гипотезу четырёх красок[10].

Все не изоморфные графы из 3 вершин и их хроматические многочлены. Пустой граф E3 (красный) допускает раскраску одним цветом, остальные — нет. Зелёный граф может быть раскрашен 3 цветами 12 способами.

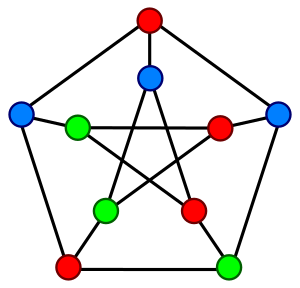
Например, граф на изображении справа может быть раскрашен 12 способами с использованием 3 цветов. Двумя цветами он не может быть окрашен в принципе. Используя 4 цвета, мы получаем 24+4*12 = 72 вариантов раскраски: при использовании всех 4 цветов, есть 4! = 24 корректных способа (каждое присвоение 4 цветов для любого графа из 4 вершин является корректным); и для каждых 3 цветов из этих 4 есть 12 способов раскраски. Тогда для графа в примере таблица чисел корректных раскрасок будет начинаться так:

Доступное число цветов 1 2 3 4 …
Количество способов раскраски 0 0 12 72 …

Для графа в примере [math]\displaystyle{ P(G,t) = t(t-1)^2(t-2) }[/math] и, конечно, [math]\displaystyle{ P(G,4) = 72 }[/math].

Хроматический многочлен содержит по меньшей мере столько же информации о раскрашиваемости [math]\displaystyle{ G }[/math], сколько и хроматическое число. В самом деле, [math]\displaystyle{ \chi }[/math] — наименьшее целое положительное число, не являющееся корнем хроматического многочлена.

[math]\displaystyle{ \chi (G)=\min\{ t\,\colon\,P(G,t) \gt 0 \}. }[/math]
Хроматические многочлены для некоторых графов
Треугольный [math]\displaystyle{ K_3 }[/math] [math]\displaystyle{ t(t-1)(t-2) }[/math]
Полный граф [math]\displaystyle{ K_n }[/math] [math]\displaystyle{ t(t-1)(t-2) \cdots (t-(n-1)) }[/math]
Дерево с [math]\displaystyle{ n }[/math] ребрами [math]\displaystyle{ t(t-1)^{n} }[/math]
Цикл [math]\displaystyle{ C_n }[/math] [math]\displaystyle{ (t-1)^n+(-1)^n(t-1) }[/math]
Граф Петерсена [math]\displaystyle{ t(t-1)(t-2)(t^7-12t^6+67t^5-230t^4+529t^3-814t^2+775t-352) }[/math]

Рёберная раскраска

Основная статья: Рёберная раскраска

Рёберная раскраска графа подразумевает под собой назначение цветов ребрам так, что никакие два ребра одного цвета не принадлежат одной вершине. Эта задача эквивалентна разделению множества граней на множества независимых граней. Наименьшее число цветов, необходимое для рёберной раскраски графа [math]\displaystyle{ G }[/math] — это его хроматический индекс, или рёберное хроматическое число, [math]\displaystyle{ \chi'(G) }[/math].

Тотальная раскраска

Основная статья: Тотальная раскраска

Тотальная раскраска — это один из видов раскраски вершин и рёбер графа. Под ней подразумевают такое присвоение цветов, что ни соседние вершины, ни смежные ребра, ни вершины и ребра, которые их соединяют, не имеют одинакового цвета. Полное хроматическое число [math]\displaystyle{ \chi''(G) }[/math] графа [math]\displaystyle{ G }[/math] — это наименьшее число цветов, необходимое для любой полной раскраски.

Свойства

Свойства хроматического многочлена

[math]\displaystyle{ P(G,t) = 1 }[/math]
  • Если граф [math]\displaystyle{ G }[/math] — объединение непересекающихся подграфов [math]\displaystyle{ H }[/math] и [math]\displaystyle{ K }[/math][11],
[math]\displaystyle{ P(G,t) = P(H,t)P(K,t) }[/math]
  • Если в [math]\displaystyle{ G }[/math] есть петля[11],
[math]\displaystyle{ P(G,t) = 0 }[/math]

Ограничения на хроматическое число

  • Назначение всем вершинам разных цветов всегда дает правильную раскраску, так что
[math]\displaystyle{ 1 \le \chi(G) \le n. }[/math]
  • Единственный вид графов, которые могут быть раскрашены одним цветом — это нулевые графы.
  • Полный граф [math]\displaystyle{ K_n }[/math], состоящий из [math]\displaystyle{ n }[/math] вершин требует [math]\displaystyle{ \chi(K_n)=n }[/math] цветов.
  • При оптимальной раскраске должно быть по меньшей мере одно ребро из [math]\displaystyle{ m }[/math] рёбер графа между каждыми двумя цветовыми классами, так что[12]
[math]\displaystyle{ \chi(G)(\chi(G)-1) \le 2m. }[/math]
  • Если [math]\displaystyle{ G }[/math] является объединением непересекающихся подграфов [math]\displaystyle{ H }[/math] и [math]\displaystyle{ K }[/math], то
[math]\displaystyle{ \chi(G) = max\{\chi(H),\chi(K)\} }[/math]
  • Если [math]\displaystyle{ G }[/math] содержит клики размера k, тогда необходимо минимум k цветов для раскраски этой клики, другими словами хроматическое число больше, либо равно кликовому числу:
[math]\displaystyle{ \chi(G) \ge \omega(G). }[/math]
Для интервальных графов это ограничение точно.
  • По теореме о четырёх красках, любой плоский граф может быть раскрашен четырьмя цветами.
  • 2-раскрашиваемые графы — это двудольные графы, в том числе и деревья.
Граф [math]\displaystyle{ G }[/math] является двудольным в том и только в том случае, если он не содержит циклов нечетной длины[11].
[math]\displaystyle{ \chi(G) \le \Delta(G) + 1. }[/math]
  • Полные графы имеют [math]\displaystyle{ \chi(G)=n }[/math] и [math]\displaystyle{ \Delta(G)=n-1 }[/math], графы-циклы имеют [math]\displaystyle{ \chi(G)=3 }[/math] и [math]\displaystyle{ \Delta(G)=2 }[/math], так что для них это ограничение является наилучшим, во всех других случаях, ограничение может быть улучшено: теорема Брукса[13] утверждает, что
[math]\displaystyle{ \chi (G) \le \Delta (G) }[/math] для связанного, простого графа [math]\displaystyle{ G }[/math], если [math]\displaystyle{ G }[/math] не является ни полным графом, ни графов-циклом.

Графы с большим хроматическим числом

  • Графы с большими кликами имеют большое хроматическое число, но обратное утверждение не всегда верно. Граф Грёча — это пример 4-раскрашиваемого графа без треугольников, и этот пример может быть обобщен на граф Мычельского.
Теорема Мычельского (Александр Зыков 1949, Ян Мычельский,1955): Существуют графы без треугольников со сколь угодно большими хроматическими числами.
  • Из теоремы Брукса, графы с большим хроматическим числом должны иметь высокую максимальную степень вершины. Другое локальное условие, из-за которого хроматическое число может быть большим — это наличие большой клики. Но раскрашиваемость графа зависит не только от локальных условий: граф с большим обхватом локально выглядит как дерево, так все циклы длинные, но его хроматическое число не равно 2:
Теорема Эрдёша: Существуют графы со сколь угодно большим обхватом и хроматическим числом[12].

Ограничения на хроматический индекс

[math]\displaystyle{ \chi'(G)=\chi(L(G)). }[/math]
  • Более того[14],
Теорема Кёнига: [math]\displaystyle{ \chi'(G) = \Delta(G) }[/math], если [math]\displaystyle{ G }[/math] — двудольный.
  • В общем случае, связь намного сильнее, чем дает теорема Брукса для раскраски вершин[14]:
Теорема Визинга: Граф с максимальной степенью вершины [math]\displaystyle{ \Delta }[/math] имеет рёберное хроматическое число [math]\displaystyle{ \Delta }[/math] или [math]\displaystyle{ \Delta+1 }[/math].

Другие свойства

  1. Если все конечные подграфы бесконечного графа [math]\displaystyle{ G }[/math] k-хроматические, то и [math]\displaystyle{ G }[/math] тоже является k-хроматическим (доказывается при предположении аксиомы выбора). Это — формулировка теоремы де Брёйна — Эрдёша[16].
  2. Если граф допускает полную n-раскраску для любого [math]\displaystyle{ n \geqslant n_0 }[/math], то он допускает бесконечную полную раскраску[17].

Открытые вопросы

Хроматическое число плоскости, в которой две точки являются смежными, если между ними единичное расстояние, неизвестно. Оно может быть равным 5, 6, или 7. Другие открытые вопросы о хроматическом числе графов включают в себя гипотезу Хадвигера, утверждающую, что любой граф с хроматическим числом k имеет полный граф из k вершин, как его минор, гипотезу Эрдёша-Фабера-Ловаса, которая ограничивает хроматическое число полных графов, которые имеют ровно одну общую вершину для каждой пары графов, и гипотезу Альбертсона о том, что среди k-хроматических графов полными являются те, которые имеют наименьшее число пересечений.

Когда Бирков и Льюис представили хроматический многочлен в их попытке решить теорему четырёх цветов, они утверждали, что для плоских графов [math]\displaystyle{ G }[/math] многочлен [math]\displaystyle{ P(G,t) }[/math] не имеет нулей в области [math]\displaystyle{ [4,\infty) }[/math]. Хотя известно, что такой хроматический многочлен не имеет нулей в области [math]\displaystyle{ [5,\infty) }[/math], и что [math]\displaystyle{ P(G,4) \neq 0 }[/math], их утверждение остается недоказанным. Так же остается открытым вопрос, как отличать графы с одинаковым хроматическим многочленом, и как определять, что многочлен является хроматическим.

Алгоритмы раскраски

Полиномиальные алгоритмы

Для двудольного графа задача раскраски вычисляется за линейное время с помощью поиска в ширину. В случае совершенных графов, хроматическое число и соответствующая ему раскраска может быть найдена за полиномиальное время при использовании полуопределённого программирования. Точные формулы для нахождения хроматического числа известны для многих классов графов (леса, циклы, колеса, хордальные графы) и так же могут быть вычислены за полиномиальное время.

Точные алгоритмы

Алгоритм полного перебора для случая k-раскраски рассматривает все [math]\displaystyle{ k^n }[/math] комбинаций расстановки цветов в графе с n вершинами и проверяет их на корректность. Чтобы вычислить хроматическое число и хроматический полином, данный алгоритм рассматривает каждое k от 1 до n. Такой алгоритм на практике может быть применим только для небольших графов.

Используя динамическое программирование и оценку размера наибольшего независимого множества, в графе возможность k-раскраски может быть разрешена за время [math]\displaystyle{ O(2,445^n) }[/math][18]. Известны более быстрые алгоритмы для 3- и 4-раскрасок, работающие за время [math]\displaystyle{ O(1,3289^n) }[/math][19] и [math]\displaystyle{ O(1,7272^n) }[/math][20] соответственно.

Стягивание

Стягивание вершин — это операция, которая из графа [math]\displaystyle{ G }[/math] делает граф [math]\displaystyle{ G/uv }[/math], отождествляя вершины [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math], удаляя соединяющие их рёбра и заменяя на одну вершину [math]\displaystyle{ w }[/math], куда перенаправляются ребра, инцидентные вершинам [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math]. Эта операция играет важную роль в анализе раскраски графов.

Хроматическое число удовлетворяет рекуррентному соотношению

[math]\displaystyle{ \chi(G) = min\{\chi(G+uv),\chi(G/uv)\} }[/math],

где [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] — несмежные вершины, [math]\displaystyle{ G + uv }[/math] — граф с добавленным ребром [math]\displaystyle{ uv }[/math]. Некоторые алгоритмы основаны на данном соотношении, выдавая как результат дерево, иногда называемое деревом Зыкова. Время выполнения зависит от метода выбора вершин [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math].

Хроматический полином удовлетворяет рекуррентному соотношению

[math]\displaystyle{ P(G - uv,t) = P(G/uv,t) + P(G,t) }[/math],

где [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] — смежные вершины, [math]\displaystyle{ G - uv }[/math] — граф с удалением ребра [math]\displaystyle{ uv }[/math]. [math]\displaystyle{ P(G - uv,t) }[/math] представляет собой число возможных правильных раскрасок графа, когда вершины [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] могут иметь одинаковые или различные цвета. Если [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] имеют разные цвета, тогда мы можем рассмотреть граф, где [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] смежные. Если [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] имеют одинаковые цвета, мы можем рассмотреть граф, где [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] объединены.

Выражения, данные выше, приводят к рекурсивной процедуре, названной алгоритм удаления и стягивания, сформировавшей основу для многих алгоритмов раскраски графов. Время работы удовлетворяет такому же рекуррентному соотношению, как и числа Фибоначчи, поэтому в наихудшем случае алгоритм будет работать за время [math]\displaystyle{ ((1 + \sqrt5)/2)^{n+m} = O(1,6180^{n+m}) }[/math] для n вершин и m рёбер[21]. На практике метод ветвей и границ и отбрасывание изоморфных графов позволяет избежать некоторых рекурсивных вызовов, время работы зависит от метода подбора пары вершин.

Жадная раскраска

Основная статья: Жадная раскраска
Два результата работы жадного алгоритма при выборе разных порядков вершин.

Жадный алгоритм упорядочивает вершины [math]\displaystyle{ v_1 }[/math],…,[math]\displaystyle{ v_n }[/math] и последовательно присваивает вершине [math]\displaystyle{ v_i }[/math] наименьший доступный цвет, не использовавшийся для окраски соседей [math]\displaystyle{ v_i }[/math] среди [math]\displaystyle{ v_1 }[/math],…,[math]\displaystyle{ v_{i-1} }[/math], либо добавляет новый. Качество полученной раскраски зависит от выбранного порядка. Всегда существует такой порядок, который приводит жадный алгоритм к оптимальному числу [math]\displaystyle{ \chi(G) }[/math] красок. С другой стороны, жадный алгоритм может быть сколь угодно плохим; например, корона с n вершинами может быть раскрашена 2 цветами, но существует порядок вершин, который приводит к жадной раскраске из [math]\displaystyle{ n/2 }[/math] цветов.

Для хордального графа и для его особых случаев (например, интервальный граф) алгоритм жадной раскраски может быть использован для нахождения оптимальной раскраски за полиномиальное время, выбирая порядок вершин обратным к совершенному порядку исключения. Этот алгоритм может быть применен и к более широкому классу графов (вполне упорядочиваемые графы), однако найти такой порядок для таких графов — NP-сложная задача.

Если вершины упорядочены в соответствии с их степенями, алгоритм жадной раскраски использует не более чем [math]\displaystyle{ max_imin\{d(v_i)+1,i\} }[/math] цветов, что максимум на 1 больше, чем [math]\displaystyle{ \Delta }[/math] (здесь [math]\displaystyle{ d(v_i) }[/math] — степень вершины [math]\displaystyle{ v_i }[/math]). Этот эвристический алгоритм иногда называют алгоритмом Уэлша-Пауэлла[22]. Другой алгоритм устанавливает порядок динамично, выбирая следующую вершину той, которая имеет наибольшее число смежных вершин разных цветов. Многие другие алгоритмы раскраски графов основаны на жадной раскраске и используют статические или динамические стратегии выбора порядка вершин.

Параллельные и распределённые алгоритмы

В области распределённых алгоритмов встречается аналогичная задача. Допустим, вершины графа — это компьютеры, которые могут общаться между собой, если они соединены ребром. Задача состоит в том, чтобы каждый компьютер выбрал для себя «цвет», так, чтобы соседние компьютеры выбрали разные цвета. Эта задача тесно связана с проблемой нарушения симметрии[англ.]. Наиболее развитые вероятностные алгоритмы работают быстрее, чем детерминированные алгоритмы для графов с достаточно большой максимальной степени вершин [math]\displaystyle{ \Delta }[/math]. Наиболее быстрые вероятностные алгоритмы используют технику множественных попыток[англ.][23].

В симметричных графах детерминированные распределённые алгоритмы не могут найти оптимальную раскраску вершин. Нужна дополнительная информация, чтобы избежать симметрии. Делается стандартное предположение, что первоначально каждая вершина имеет уникальный идентификатор, например, из множества [math]\displaystyle{ \{1, 2, ..., N\} }[/math]. Иными словами, предполагается, что нам дана n-раскраска. Задача состоит в том, чтобы уменьшить количество цветов от n до, например, [math]\displaystyle{ (\Delta + 1) }[/math]. Чем больше цветов используются (например, [math]\displaystyle{ O(\Delta) }[/math] вместо [math]\displaystyle{ (\Delta + 1) }[/math]), тем меньше обменов сообщений потребуется[23].

Простая версия распределённого жадного алгоритма для [math]\displaystyle{ (\Delta + 1) }[/math] -раскраски требует [math]\displaystyle{ \Theta(n) }[/math] раундов связи в худшем случае — информации, возможно, придется проходить с одного конца стороны сети до другого.

Наиболее простым интересным случаем является n-цикл. Ричард Коул и Узи Вишкин[24] показали, что существует распределённый алгоритм, который уменьшает количество цветов от n до [math]\displaystyle{ O(log(n)) }[/math], используя лишь один раз обмен сообщениями между соседями. Повторяя ту же процедуру, можно получить 3-раскраску n-цикла за [math]\displaystyle{ O(log^*(n)) }[/math] раундов связи (при условии, что даны уникальные идентификаторы узлов).

Функция [math]\displaystyle{ log^* }[/math], итерированный логарифм, является чрезвычайно медленно растущей функцией, «почти константа». Следовательно, результаты Коула и Вишкина поднимают вопрос о том, есть ли распределённый алгоритм 3-раскраски n-цикла, который выполняется за константное время. Натан Линиал показал, что это невозможно: любой детерминированный распределённый алгоритм требует [math]\displaystyle{ \Omega(log^*(n)) }[/math] раундов связи для уменьшения N-раскраски до 3-раскраски в n-цикле[25].

Техника Коула и Вишкина также может быть применена для произвольного графа с ограниченной степенью вершин, в этом случае время работы составляет [math]\displaystyle{ P(\Delta) + O(log^*(n)) }[/math][26]. Этот метод был обобщен для графа единичных кругов Шнайдером и др[27].

Проблема раскраски рёбер также изучалась в распределённой модели. Пансонецци и Рицци достигли [math]\displaystyle{ (2\Delta - 1) }[/math]-раскраски за [math]\displaystyle{ O(\Delta + log^*(n)) }[/math] в этой модели[28]. Нижняя граница для распределённой раскраски вершин, достигнутая Линиалом, также применима для задачи распределённой раскраски рёбер[25].

Децентрализованные алгоритмы

Децентрализованными называются алгоритмы, в которых не разрешена внутренняя передача сообщений (в отличие от распределённых алгоритмов, где процессы обмениваются между собой данными). Существуют эффективные децентрализованные алгоритмы, успешно справляющиеся с задачей раскраски графов. Эти алгоритмы работают в предположении, что вершина способна «чувствовать», что какая-либо из её соседних вершин раскрашена в тот же цвет, что и она. Другими словами, есть возможность определить локальный конфликт. Такое условие довольно часто выполняется в реальных прикладных задачах — например, при передаче данных по беспроводному каналу передающая станция, как правило, имеет возможность детектировать, что другая станция пытается передавать одновременно в тот же канал. Способности к получению подобной информации достаточно для того, чтобы алгоритмы, основанные на обучающихся автоматах[англ.], с вероятностью единица правильно решат задачу раскраски графа[29][30].

Сложность вычислений

Раскраска графа является вычислительно сложной задачей. Узнать, допускает ли граф k-раскраску для заданного k — это NP-полная задача, кроме случаев k = 1 и k = 2. В частности, задача вычисления хроматического числа NP-сложна[31]. Задача о 3-раскраске NP-полная даже для случая планарного графа степени 4[32].

Также NP-сложной задачей является раскраска 3-раскрашиваемого графа 4 цветами[33] и k-раскрашиваемого графа [math]\displaystyle{ k^{log(k)/25} }[/math] при достаточно больших значениях k[34].

Вычисление коэффициентов хроматического полинома #P-сложная задача. Доказано, что не существует ни одного FPRAS-алгоритма для вычисления хроматического полинома ни для какого рационального числа k ≥ 1,5, кроме k = 2, если только не выполнится, что NP = RP[35].

Применение

Основная статья: Практическое применение раскраски графов

Планирование

Раскраска вершин моделирует многие проблемы планирования[36]. В своей простейшей постановке заданный набор работ должен быть распределен по временным отрезкам, каждая такая работа занимает один отрезок. Они могут быть выполнены в любом порядке, но две работы могут конфликтовать в том смысле, что не могут быть выполнены одновременно, так как, например, используют общие ресурсы. Соответствующий граф содержит вершину для каждой из работ и ребро для каждой конфликтующей пары. Хроматическое число построенного графа — это минимальное время выполнения всех работ без конфликтов.

Детали проблемы планирования определяют структуру графа. Например, когда идет распределение самолётов по рейсам, результирующий граф конфликтов является интервальным графом, так что проблема раскраски может быть решена эффективно. При распределении радиочастот получается граф единичных кругов конфликтов, и для такой задачи существует 3-аппроксимационный алгоритм.

Распределение регистров

Основная статья: Распределение регистров

Компилятор — это компьютерная программа, которая переводит один компьютерный язык в другой. Для улучшения времени выполнения результирующего кода одной из техник компиляторной оптимизации, является распределение регистров, в которой наиболее часто используемые переменные компилируемой программы хранятся в быстродействующих регистрах процессора. В идеальном случае переменные хранятся в регистрах так, что они все находятся в регистрах во время их использования.

Стандартный подход к этой задаче состоит в сведении её к задаче раскраски графов[8]. Компилятор строит интерференционный граф, где вершины соответствуют переменным, а грань соединяет две из них, если они нужны в один и тот же момент времени. Если этот граф k-хроматический, то переменные могут храниться в k регистрах.

Цифровые водяные знаки

Технология цифровых водяных знаков (англ. digital watermarking) позволяет вместе с данными (будь то медиафайлы, исполняемые файлы и прочие) передать некое скрытое сообщение («водяной знак», Watermark). Такое скрытое сообщение может быть применено в защите авторских прав для идентификации владельца данных.

Это важно, например, для установления источника их распространения нелегальным образом. Или же для подтверждения прав на данные, например — программное обеспечение систем на кристалле (system-on-chip).

Сообщение можно закодировать в том числе и в способе распределения регистров. Одну из таких техник предложили Qu и Potkonjak[37] (поэтому её иногда называют QP-алгоритмом).

Состоит она вот в чём: пусть [math]\displaystyle{ G }[/math] — граф несовместимости (интерференционный граф) распределения регистров процессора, о котором говорилось выше. Его раскраска используется в программе — причём, используется так, что допустимо поменять содержимое графа с небольшим увеличением его хроматического числа. Оказывается возможно закодировать послание в программном продукте с помощью раскраски графа [math]\displaystyle{ G }[/math], то есть распределения регистров.

Извлечь это сообщение можно путём сравнением распределения регистров с исходной раскраской;[38] существуют и способы удостовериться в том, было ли некое сообщение закодировано в программе без использования исходного.

В дальнейшем разные авторы развивали и уточняли идеи Qu и Potkonjak[39].[38][40]

Другие применения

Задача раскраски графов была поставлена во многих других областях применения, включая сопоставление с образцом.

Решение головоломки судоку можно рассматривать как завершение раскраски 9 цветами заданного графа из 81 вершины.

Примечания

  1. ↑ 1,0 1,1 1,2 (Molloy & Reed 2002, The Basic Definitions)
  2. ↑ (Донец & Шор 1982, Историческая справка)
  3. ↑ (Kubale 2004, History of graph coloring)
  4. ↑ (van Lint & Wilson 2001, Chap. 33)
  5. ↑ (Jensen & Toft 1995, С. 2)
  6. ↑ C.E. Shannon, "The zero-error capacity of a noisy channel, " IEEE Trans. Information Theory, pp. 8-19, 1956.
  7. ↑ (Зыков 1949)
  8. ↑ 8,0 8,1 (Chaitin 1982)
  9. ↑ A.O.Ivanov, A.A.Tuzhilin (2019), The Gromov-Hausdorff Distance between Simplexes and Two-Distance Spaces, <https://arxiv.org/pdf/1907.09942.pdf>  Архивная копия от 29 июля 2019 на Wayback Machine
  10. ↑ (Birkhoff & Lewis 1946)
  11. ↑ 11,0 11,1 11,2 11,3 (Tutte 1984, Chromatic polynomial)
  12. ↑ 12,0 12,1 12,2 (Diestel 2005, Colouring vertices)
  13. ↑ (Brooks & Tutte 1941)
  14. ↑ 14,0 14,1 (Diestel 2005, Colouring edges)
  15. ↑ (Nešetřil & Ossona de Mendez 2012)
  16. ↑ (de Bruijn, Erdős 1951)
  17. ↑ (Fawcett 1978)
  18. ↑ (Lawler 1976)
  19. ↑ (Beigel & Eppstein 2005)
  20. ↑ (Fomin, Gaspers & Saurabh 2007)
  21. ↑ (Sekine, Imai & Tani 1995)
  22. ↑ (Welsh & Powell 1967)
  23. ↑ 23,0 23,1 (Schneider 2010)
  24. ↑ (Cole & Vishkin 1986), см. также (Cormen, Leiserson & Rivest 1990, Section 30.5)
  25. ↑ 25,0 25,1 (Linial 1992)
  26. ↑ (Goldberg, Plotkin & Shannon 1988)
  27. ↑ (Schneider 2008)
  28. ↑ (Panconesi & Rizzi 2001)
  29. ↑ (Leith & Clifford 2006)
  30. ↑ (Duffy, O'Connell & Sapozhnikov 2008)
  31. ↑ (Garey, Johnson & Stockmeyer 1974); (Garey & Johnson 1979).
  32. ↑ (Dailey 1980)
  33. ↑ (Guruswami & Khanna 2000)
  34. ↑ (Khot 2001)
  35. ↑ (Goldberg & Jerrum 2008)
  36. ↑ (Marx 2004)
  37. ↑ (Qu & Potkonjak 1998)
  38. ↑ 38,0 38,1 (Zhu & Thomborson 2006)
  39. ↑ (Collberg, Thomborson & Townsend 2004)
  40. ↑ (Myles & Collberg 2003)

Литература

Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Раскраска_графов&oldid=12495790