Функтор (математика)

Функтор — особый тип отображений между категориями. Его можно понимать как отображение, сохраняющее структуру. Функторы между малыми категориями являются морфизмами в категории малых категорий. Совокупность всех категорий не является категорией в обычном смысле, так как совокупность её объектов не является классом. Один из способов преодолеть подобные теоретико-множественные трудности — добавление в ZFC независимой от неё аксиомы о существовании недостижимых кардиналов.

Впервые функторы начали рассматривать в алгебраической топологии, в которой топологическим пространствам сопоставляются алгебраические объекты (например, фундаментальная группа), а непрерывным отображениям — гомоморфизмы между этими объектами. Впоследствии функторы получили распространение во многих областях математики и используются для того, чтобы связывать между собой различные категории.

Термин «функтор» был позаимствован математиками из работ философа Рудольфа Карнапа, при этом у Карнапа слово «функтор» относилось к лингвистическому понятию.

Определение

Функтор [math]\displaystyle{ F }[/math] должен сохранять композицию морфизмов [math]\displaystyle{ \tau }[/math] и [math]\displaystyle{ \sigma }[/math]

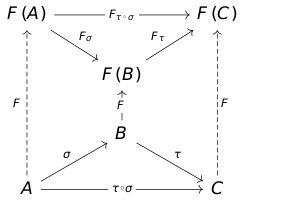
(Ковариантный) функтор [math]\displaystyle{ \mathcal{F}\colon\mathcal{C}\to \mathcal{D} }[/math] из категории [math]\displaystyle{ \mathcal{C} }[/math] в категорию [math]\displaystyle{ \mathcal{D} }[/math] — это отображение, которое:

• сопоставляет каждому объекту [math]\displaystyle{ X\in\mathcal{C} }[/math] объект [math]\displaystyle{ \mathcal{F}(X)\in\mathcal{D}, }[/math]
• сопоставляет каждому морфизму [math]\displaystyle{ f:X\to Y }[/math] в категории [math]\displaystyle{ \mathcal{C} }[/math] морфизм [math]\displaystyle{ \mathcal{F}(f): \mathcal{F}(X) \to \mathcal{F}(Y) }[/math] в категории [math]\displaystyle{ \mathcal{D} }[/math]. Это сопоставление должно обладать следующими свойствами:
  • [math]\displaystyle{ \mathcal{F}(\mathrm{id}_A) = \mathrm{id}_{\mathcal{F}(A)} }[/math],
  • [math]\displaystyle{ \mathcal{F}(g\circ f) = \mathcal{F}(g)\circ \mathcal{F}(f) }[/math].

Таким образом, функтор должен сохранять тождественные морфизмы и структуру композиции морфизмов.

Аналогичным образом, контравариантный функтор — это отображение, обращающее стрелки (то есть сопоставляющее морфизму [math]\displaystyle{ f:X\to Y }[/math] морфизм [math]\displaystyle{ \mathcal{F}(f): \mathcal{F}(Y) \to \mathcal{F}(X) }[/math]), сохраняющее тождественные морфизмы и удовлетворяющее равенству:

[math]\displaystyle{ \mathcal{F}(g\circ f) = \mathcal{F}(f)\circ \mathcal{F}(g) }[/math].

Также контравариантный функтор можно определить как ковариантный функтор из двойственной категории [math]\displaystyle{ \mathcal{C}^\mathrm{op} }[/math]. Некоторые авторы предпочитают записывать все выражения ковариантно, и вместо слов «контравариантный функтор из [math]\displaystyle{ \mathcal{C} }[/math] в [math]\displaystyle{ \mathcal{D} }[/math]» говорят «функтор из [math]\displaystyle{ \mathcal{C}^\mathrm{op} }[/math] в [math]\displaystyle{ \mathcal{D} }[/math]» (или, иногда, «функтор из [math]\displaystyle{ \mathcal{C} }[/math] в [math]\displaystyle{ \mathcal{D}^\mathrm{op} }[/math]»).

Бифункторы и мультифункторы

Бифунктор — это функтор от двух аргументов. Естественный пример — функтор Hom, он ковариантен по одному аргументу и контравариантен по другому.

Формально бифункторы определяются как функторы из категории произведения. Например, функтор [math]\displaystyle{ \mathrm{Hom} }[/math] имеет вид [math]\displaystyle{ \mathcal C^\mathrm{op} \times \mathcal C \to \mathbf{Set} }[/math].

Мультифунктор — это обобщение понятия бифунктора на [math]\displaystyle{ n }[/math] переменных.

Примеры

Для задания функтора нужно определить действие его не только на объектах категории, но и (что более важно) на морфизмах: существуют различные функторы, действующие одинаково на объектах, например, тождественный функтор и антитождественный функтор, обращающий стрелки.

• Пусть [math]\displaystyle{ \mathcal{C} }[/math] — подкатегория в категории [math]\displaystyle{ \mathcal{D} }[/math]. В таком случае определён функтор вложения [math]\displaystyle{ I: \mathcal{C} \hookrightarrow \mathcal{D} }[/math], действующий на объектах и морфизмах как соответствующие вложения классов.
• Постоянный функтор: функтор, отображающий каждый объект категории [math]\displaystyle{ \mathcal{C} }[/math] в фиксированный объект категории [math]\displaystyle{ \mathcal{D} }[/math], а каждый морфизм [math]\displaystyle{ \mathcal{C} }[/math] — в тождественный морфизм этого объекта.
• Эндофункторами называют любые функторы из категории в себя.
• Двойственное векторное пространство: отображение, сопоставляющее каждому векторному пространству двойственное к нему, а каждому линейному отображению — двойственное (или транспонированное) отображение, является контравариантным эндофунктором на категории векторных пространств.
• Пусть [math]\displaystyle{ \mathcal{C} }[/math] — конкретная категория, то есть категория, снабженная унивалентным функтором в категорию множеств (частный случай забывающего функтора). С помощью этого функтора объектам категории сопосталяются множества, и можно думать о морфизмах, как о функциях на этих множествах, сохраняющих дополнительную структуру (пример: категории групп, категория колец, категория множеств). Левый сопряжённый (если он существует) к забывающему функтору есть функтор свободного объекта (пример: свободный модуль).
• Предпучки: пусть [math]\displaystyle{ X }[/math] — топологическое пространство, тогда открытые подмножества [math]\displaystyle{ X }[/math] образуют частично упорядоченное множество по отношению включения, обозначаемое [math]\displaystyle{ O(X) }[/math]. Как и любому частично упорядоченному множеству, [math]\displaystyle{ O(X) }[/math] можно сопоставить категорию, добавляя единственный морфизм [math]\displaystyle{ U \to V }[/math] тогда и только тогда, когда [math]\displaystyle{ U\subseteq V }[/math]. Контравариантные функторы из [math]\displaystyle{ O(X) }[/math] называются предпучками. Например, существует функтор в категорию действительных алгебр, сопоставляющий открытому множеству алгебру вещественнозначных непрерывных функций на нём.
• Фундаментальная группа: каждому топологическому пространству [math]\displaystyle{ X }[/math] с отмеченной точкой [math]\displaystyle{ x_0 }[/math] можно сопоставить фундаментальную группу [math]\displaystyle{ \pi_1(X, x_0) }[/math], элементы которой — классы эквивалентности петель с точностью до гомотопии. Если [math]\displaystyle{ f: X \to (Y) }[/math] — морфизм пространств с отмеченной точкой (непрерывное отображение, переводящее отмеченную точку первого пространства в отмеченную точку второго), каждой петле из точки [math]\displaystyle{ x_0 }[/math] можно сопоставить её образ, являющийся петлёй из точки [math]\displaystyle{ y_0 }[/math]. Это сопоставление согласуется с классами эквивалентности и с операцией композиции, следовательно, является гомоморфизмом из [math]\displaystyle{ \pi(X, x_0) }[/math] в [math]\displaystyle{ \pi(Y, y_0) }[/math]. Нетрудно проверить, что выполняются и все остальные свойства ковариантного функтора из категории топологических пространств с отмеченной точкой в категорию групп.
• Касательное и кокасательное расслоение: отображение, сопоставляющее гладкому многообразию его касательное расслоение, а диффеоморфизму многообразий — его дифференциал, является ковариантным функтором из категории гладких многообразий и диффеоморфизмов в категорию векторных расслоений. Аналогично, кокасательное расслоение и кодифференциал диффеоморфизма задают контравариантный функтор.

  Рассмотрение касательного пространства в фиксированной точке задаёт ковариантный функтор из категории гладких многообразий с отмеченной точкой и гладких отображений в категорию векторных пространств.

• Тензорное произведение: если [math]\displaystyle{ \mathcal{C} }[/math] — категория векторных пространств над фиксированным полем, тензорное произведение двух пространств задаёт функтор [math]\displaystyle{ \mathcal{C} \times \mathcal{C} \to \mathcal{C} }[/math], ковариантный по обоим аргументам.
• Симплициальные объекты — произвольные контравариантные функторы из симплициальной категории в различные категории (в категорию множеств — симплициальное множество, в категорию групп — симплициальная группа и другие); конструкции, обобщающие понятие симплициального комплекса, играют важную роль в алгебраической топологии.
• Функтор [math]\displaystyle{ \operatorname{Gal}: \mathbf{Fld}^\mathrm{op} \to \mathbf{Grp} }[/math] сопоставляет полю [math]\displaystyle{ F }[/math] его абсолютную группу Галуа [math]\displaystyle{ \operatorname{Gal}(\bar F / F) }[/math], а гомоморфизму полей — соответствующий^{[прояснить]} гомоморфизм групп Галуа.

Свойства

• Функтор переводит коммутативные диаграммы в коммутативные диаграммы.
• Функтор переводит изоморфизмы в изоморфизмы.
• Композиция двух функторов тоже является функтором. Композиция функторов является ассоциативной операцией (там, где она определена), поэтому функторы между малыми категориями удовлетворяют всем свойствам морфизмов в категории.

Категория из одного объекта — то же самое, что моноид: морфизмы в ней соответствуют элементам моноида, а операция композиции морфизмов — операции, определённой в моноиде. Функторы между категориями с одним объектом взаимно однозначно соответствуют гомоморфизмам моноидов; следовательно, в некотором смысле функтор является обобщением понятия гомоморфизма моноидов на «моноиды, в которых операция композиции определена не всюду».

Связь с другими категорными понятиями

Пусть [math]\displaystyle{ \mathcal{C} }[/math] и [math]\displaystyle{ \mathcal{D} }[/math] — категории. Множество всех морфизмов [math]\displaystyle{ \mathcal{F}\colon\mathcal{C}\to \mathcal{D} }[/math] можно считать множеством объектов другой категории: категории функторов. Морфизмы в этой категории — естественные преобразования функторов.

Функторы довольно часто задают при помощи универсальных свойств, примеры включают в себя тензорные произведения, произведения групп, множеств или векторных пространств, прямые и обратные пределы. Также универсальные конструкции часто задают пару сопряжённых функторов.

Литература

• Букур И., Деляну А. . Введение в теорию категорий и функторов. — М.: Мир, 1972. — 259 с.
• Маклейн С. . Глава 2. Конструкции в категориях // Категории для работающего математика. — М.: Физматлит, 2004. — 352 с. — ISBN 5-9221-0400-4. — С. 43—67.
• Цаленко М. С., Шульгейфер Е. Г. . Основы теории категорий. — М.: Наука, 1974. — 256 с.

Ссылки

• Marquis, Jean-Pierre. Category Theory (англ.). Stanford Encyclopedia of Philosophy. — Включает в себя очень полный список литературы. Дата обращения: 30 июля 2013. Архивировано 13 августа 2013 года.