Поверхность

Пример простой поверхности

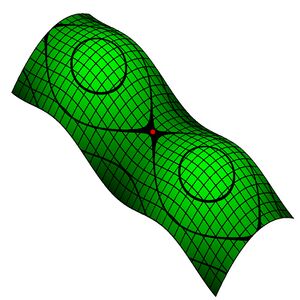
Пове́рхность в геометрии и топологии — двумерное топологическое многообразие. Наиболее известными примерами поверхностей являются границы геометрических тел в обычном трёхмерном евклидовом пространстве. С другой стороны, существуют поверхности (например, бутылка Клейна), которые нельзя вложить в трёхмерное евклидово пространство без привлечения сингулярности или самопересечения.

«Двумерность» поверхности подразумевает возможность реализовать на ней метод координат, хотя и необязательно для всех точек. Так, поверхность Земли (в идеале) представляет собой двумерную сферу, широта и долгота каждой точки которой являются её координатами (за исключением полюсов и 180-го меридиана).

Концепция поверхности применяется в физике, инженерном деле, компьютерной графике и прочих областях при изучении физических объектов. Например, анализ аэродинамических качеств самолёта базируется на обтекании потоком воздуха его поверхности.

Способы задания

Поверхность определяется как множество точек, координаты которых удовлетворяют определённому виду уравнений:

[math]\displaystyle{ F(x,\,y,\,z)=0\qquad (1) }[/math]

Если функция [math]\displaystyle{ F(x,\,y,\,z) }[/math] непрерывна в некоторой точке и имеет в ней непрерывные частные производные, по крайней мере одна из которых не обращается в нуль, то в окрестности этой точки поверхность, заданная уравнением (1), будет правильной поверхностью.

Помимо указанного выше неявного способа задания, поверхность может быть определена явно, если одну из переменных, например, z, можно выразить через остальные:

[math]\displaystyle{ z=f(x,y)\qquad (1') }[/math]

Также существует параметрический способ задания. В этом случае поверхность определяется системой уравнений:

[math]\displaystyle{ \left\{ \begin{array}{ccc} x &=& x(u,v) \\ y &=& y(u,v) \\ z &=& z(u,v) \end{array}\right.\qquad (1'') }[/math]

Понятие о простой поверхности

Основная статья: Простая поверхность

Интуитивно простую поверхность можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям).

Более строго, простой поверхностью называется образ гомеоморфного отображения (то есть взаимно однозначного и взаимно непрерывного отображения) внутренности единичного квадрата. Этому определению можно дать аналитическое выражение.

Пусть на плоскости с прямоугольной системой координат u и v задан квадрат, координаты внутренних точек которого удовлетворяют неравенствам 0 < u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u', v') были различными соответствующие точки (x, у, z) и (x', у', z').

Примером простой поверхности является полусфера. Вся же сфера не является простой поверхностью. Это вызывает необходимость дальнейшего обобщения понятия поверхности.

Подмножество пространства, у каждой точки которого есть окрестность, являющаяся простой поверхностью, называется правильной поверхностью.

Поверхность в дифференциальной геометрии

Основная статья: Дифференциальная геометрия поверхностей

В дифференциальной геометрии исследуемые поверхности обычно подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Как правило, это — условия гладкости поверхности, то есть существования в каждой точке поверхности определённой касательной плоскости, кривизны и т. д. Эти требования сводятся к тому, что функции, задающие поверхность, предполагаются однократно, дважды, трижды, а в некоторых вопросах — неограниченное число раз дифференцируемыми или даже аналитическими функциями. При этом дополнительно накладывается условие регулярности.

Случай неявного задания. Поверхность, заданная уравнением [math]\displaystyle{ F(x,\,y,\,z)=0,\; F:\Omega\to\mathbb{R}^3 }[/math], является гладкой регулярной поверхностью, если [math]\displaystyle{ \exist P_0(x_0,\,y_0,\,z_0):\;F(x_0,\,y_0,\,z_0)=0 }[/math], функция [math]\displaystyle{ F }[/math] непрерывно дифференцируема в своей области определения [math]\displaystyle{ \Omega }[/math], а её частные производные одновременно не обращаются в нуль (условие правильности) на всём множестве [math]\displaystyle{ \Omega }[/math]:

[math]\displaystyle{ \left( \frac{\partial F}{\partial x}\right)^2+\left( \frac{\partial F}{\partial y}\right)^2+\left( \frac{\partial F}{\partial z}\right)^2\gt 0 }[/math]

Случай параметрического задания. Зададим поверхность векторным уравнением [math]\displaystyle{ \mathbf{r} = \mathbf{r}(u,\ v) }[/math], или, что то же самое, тремя уравнениями в координатах:

[math]\displaystyle{ \left\{ \begin{array}{ccc} x &=& x(u,v) \\ y &=& y(u,v) \\ z &=& z(u,v) \end{array}\right.\quad (u,\,v)\in\Omega }[/math]

Эта система уравнений задаёт гладкую регулярную поверхность, если выполнены условия:

• система устанавливает взаимно однозначное соответствие между образом и прообразом [math]\displaystyle{ \Omega }[/math];
• функции [math]\displaystyle{ x(u,v),\,y(u,v),\,z(u,v) }[/math] непрерывно дифференцируемы в [math]\displaystyle{ \Omega }[/math];
• выполнено условие невырожденности:

[math]\displaystyle{ \begin{vmatrix}x'_u & x'_v \\ y'_u & y'_v \end{vmatrix}^2+\begin{vmatrix}y'_u & y'_v \\ z'_u & z'_v \end{vmatrix}^2+\begin{vmatrix}z'_u & z'_v \\ x'_u & x'_v \end{vmatrix}^2\gt 0 }[/math]

Геометрически последнее условие означает, что векторы [math]\displaystyle{ \frac{\partial\mathbf{r}} {\partial u}, \frac{\partial\mathbf{r}} {\partial v} }[/math] нигде не параллельны.

Координатная сетка на сфере

Параметры u, v можно рассматривать как внутренние координаты точек поверхности. Фиксируя одну из координат, мы получаем два семейства координатных кривых, покрывающих поверхность координатной сеткой.

Случай явного задания. Поверхность [math]\displaystyle{ S }[/math] может быть определена как график функции [math]\displaystyle{ z=f(x,y) }[/math]; тогда [math]\displaystyle{ S }[/math] является гладкой регулярной поверхностью, если функция [math]\displaystyle{ f }[/math] дифференцируема. Этот вариант можно рассматривать как частный случай параметрического задания: [math]\displaystyle{ x=u;\ y=v;\ z=f(u,v) }[/math].

Касательная плоскость

Касательная плоскость в точке поверхности.

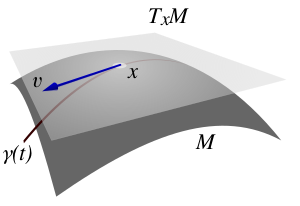
Касательная плоскость в точке гладкой поверхности — это плоскость, имеющая максимальный порядок соприкосновения с поверхностью в этой точке. Эквивалентный вариант определения: касательная плоскость есть плоскость, содержащая касательные ко всем гладким кривым, проходящим через эту точку.

Пусть гладкая кривая на параметрически заданной поверхности [math]\displaystyle{ \mathbf{r} = \mathbf{r}(u,\ v) }[/math] задана в виде:

[math]\displaystyle{ u = u(t);\ v = v(t) }[/math].

Направление [math]\displaystyle{ \mathbf{v} }[/math] касательной к такой кривой даёт вектор:

[math]\displaystyle{ \mathbf{v} = \frac{d\mathbf{r}}{dt}=\frac{\partial\mathbf{r}}{\partial u} \frac{du}{dt} + \frac{\partial\mathbf{r}}{\partial v} \frac{dv}{dt} }[/math]

Отсюда видно, что все касательные ко всем кривым в данной точке лежат в одной плоскости, содержащей векторы [math]\displaystyle{ \frac{\partial\mathbf{r}} {\partial u}, \frac{\partial\mathbf{r}} {\partial v} }[/math], которые мы выше предположили независимыми.

Уравнение касательной плоскости в точке [math]\displaystyle{ \mathbf{r_0}=(x_0, y_0, z_0) }[/math] имеет вид:

[math]\displaystyle{ \left(\mathbf{r} - \mathbf{r_0}, \frac{\partial\mathbf{r}} {\partial u}, \frac{\partial\mathbf{r}} {\partial v}\right) = 0\quad }[/math] (смешанное произведение векторов).

В координатах уравнения касательной плоскости для разных способов задания поверхности приведены в таблице:

	касательная плоскость к поверхности в точке [math]\displaystyle{ (x_0,y_0,z_0) }[/math]
неявное задание	[math]\displaystyle{ \frac{\partial F}{\partial x}(x-x_0)+\frac{\partial F}{\partial y}(y-y_0)+\frac{\partial F}{\partial z}(z-z_0)=0 }[/math]
явное задание	[math]\displaystyle{ \frac{\partial f}{\partial x}(x-x_0)+\frac{\partial f}{\partial y}(y-y_0)=(z-z_0) }[/math]
параметрическое задание	[math]\displaystyle{ \begin{vmatrix} x-x_0 & y-y_0 & z-z_0 \\ x_u' & y_u' & z_u' \\ x_v' & y_v' & z_v' \end{vmatrix} = 0 }[/math]

Все производные берутся в точке [math]\displaystyle{ (x_0,y_0,z_0) }[/math].

Метрика и внутренняя геометрия

Вновь рассмотрим гладкую кривую:

[math]\displaystyle{ u = u(t);\ v = v(t) }[/math].

Элемент её длины определяется из соотношения:

[math]\displaystyle{ ds^2 = |d\mathbf{r}|^2 = \left(\frac{\partial\mathbf{r}}{\partial u} du + \frac{\partial\mathbf{r}}{\partial v} dv\right)^2 = E\,du^2 + 2 F\,du\,dv + G\,dv^2 }[/math],

где [math]\displaystyle{ E=\mathbf{r'_u}\mathbf{r'_u};\ F=\mathbf{r'_u}\mathbf{r'_v};\ G=\mathbf{r'_v}\mathbf{r'_v} }[/math].

Эта квадратичная форма называется первой квадратичной формой и представляет собой двумерный вариант метрики поверхности. Для регулярной поверхности её дискриминант [math]\displaystyle{ EG-F^2\gt 0 }[/math] во всех точках. Коэффициент [math]\displaystyle{ F=0 }[/math] в точке поверхности тогда и только тогда, когда в этой точке координатные кривые ортогональны. В частности, на плоскости с декартовыми координатами [math]\displaystyle{ u,\ v }[/math] получается метрика [math]\displaystyle{ ds^2 = du^2 + dv^2 }[/math] (теорема Пифагора).

Геликоид

Катеноид

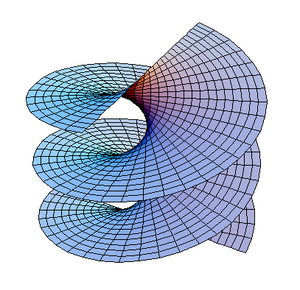
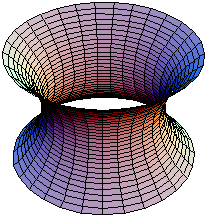
Метрика не определяет однозначно форму поверхности. Например, метрики геликоида и катеноида, параметризованных соответствующим образом, совпадают, то есть между их областями существует соответствие, сохраняющее все длины (изометрия). Свойства, сохраняющиеся при изометрических преобразованиях, называются внутренней геометрией поверхности. Внутренняя геометрия не зависит от положения поверхности в пространстве и не меняется при её изгибании без растяжения и сжатия (например, при изгибании цилиндра в конус).

Метрические коэффициенты [math]\displaystyle{ E,\ F,\ G }[/math] определяют не только длины всех кривых, но и вообще результаты всех измерений внутри поверхности (углы, площади, кривизна и др.). Поэтому всё, что зависит только от метрики, относится к внутренней геометрии.

Нормаль и нормальное сечение

Векторы нормали в точках поверхности

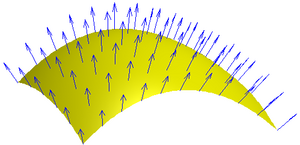
Одной из основных характеристик поверхности является её нормаль — единичный вектор, перпендикулярный касательной плоскости в заданной точке:

[math]\displaystyle{ \mathbf{m} = \frac{[\mathbf{r'_u}, \mathbf{r'_v}]} {|[\mathbf{r'_u}, \mathbf{r'_v}]|} }[/math].

Знак нормали зависит от выбора координат.

Сечение поверхности плоскостью, содержащей нормаль поверхности в заданной точке, образует некоторую кривую, которая называется нормальным сечением поверхности. Главная нормаль для нормального сечения совпадает с нормалью к поверхности (с точностью до знака).

Если же кривая на поверхности не является нормальным сечением, то её главная нормаль образует с нормалью поверхности некоторый угол [math]\displaystyle{ \theta }[/math]. Тогда кривизна [math]\displaystyle{ k }[/math] кривой связана с кривизной [math]\displaystyle{ k_n }[/math] нормального сечения (с той же касательной) формулой Мёнье:

[math]\displaystyle{ k_n = \pm k\,\cos\,\theta }[/math]

Координаты орта нормали для разных способов задания поверхности приведены в таблице:

	Координаты нормали в точке поверхности
неявное задание	[math]\displaystyle{ \frac{\left(\frac{\partial F}{\partial x};\,\frac{\partial F}{\partial y};\,\frac{\partial F}{\partial z}\right)}{\sqrt{\left(\frac{\partial F}{\partial x}\right)^2+\left( \frac{\partial F}{\partial y}\right)^2+\left( \frac{\partial F}{\partial z}\right)^2}} }[/math]
явное задание	[math]\displaystyle{ \frac{\left(-\frac{\partial f}{\partial x};\,-\frac{\partial f}{\partial y};\,1\right)}{\sqrt{\left(\frac{\partial f}{\partial x}\right)^2+\left( \frac{\partial f}{\partial y}\right)^2+1}} }[/math]
параметрическое задание	[math]\displaystyle{ \frac{\left(\frac{D(y,z)}{D(u,v)};\,\frac{D(z,x)}{D(u,v)};\,\frac{D(x,y)}{D(u,v)}\right)}{\sqrt{\left(\frac{D(y,z)}{D(u,v)}\right)^2+\left(\frac{D(z,x)}{D(u,v)}\right)^2+\left(\frac{D(x,y)}{D(u,v)}\right)^2}} }[/math]

Здесь [math]\displaystyle{ \frac{D(y,z)}{D(u,v)}=\begin{vmatrix}y'_u & y'_v \\ z'_u & z'_v \end{vmatrix},\quad\frac{D(z,x)}{D(u,v)}=\begin{vmatrix} z'_u & z'_v\\ x'_u & x'_v \end{vmatrix},\quad\frac{D(x,y)}{D(u,v)}=\begin{vmatrix}x'_u & x'_v \\ y'_u & y'_v \end{vmatrix} }[/math].

Все производные берутся в точке [math]\displaystyle{ (x_0,y_0,z_0) }[/math].

Кривизна

Для разных направлений в заданной точке поверхности получается разная кривизна нормального сечения, которая называется нормальной кривизной; ей приписывается знак плюс, если главная нормаль кривой идёт в том же направлении, что и нормаль к поверхности, или минус, если направления нормалей противоположны.

Вообще говоря, в каждой точке поверхности существуют два перпендикулярных направления [math]\displaystyle{ e_1 }[/math] и [math]\displaystyle{ e_2 }[/math], в которых нормальная кривизна принимает минимальное и максимальное значения; эти направления называются главными. Исключение составляет случай, когда нормальная кривизна по всем направлениям одинакова (например, у сферы или на торце эллипсоида вращения), тогда все направления в точке — главные.

Поверхности с отрицательной (слева), нулевой (в центре) и положительной (справа) кривизной.

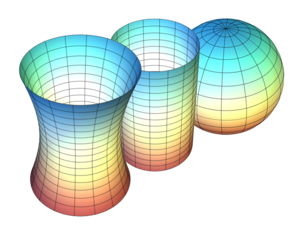
Нормальные кривизны в главных направлениях называются главными кривизнами; обозначим их [math]\displaystyle{ \kappa_1 }[/math] и [math]\displaystyle{ \kappa_2 }[/math]. Величина:

[math]\displaystyle{ K=\kappa_1\kappa_2 }[/math]

называется гауссовой кривизной, полной кривизной или просто кривизной поверхности. Встречается также термин скаляр кривизны, который подразумевает результат свёртки тензора кривизны; при этом скаляр кривизны вдвое больше, чем гауссова кривизна.

Гауссова кривизна может быть вычислена через метрику, и поэтому она является объектом внутренней геометрии поверхностей (отметим, что главные кривизны к внутренней геометрии не относятся). По знаку кривизны можно классифицировать точки поверхности (см. рисунок). Кривизна плоскости равна нулю. Кривизна сферы радиуса R всюду равна [math]\displaystyle{ \frac{1}{R^2} }[/math]. Существует и поверхность постоянной отрицательной кривизны — псевдосфера.

Геодезические линии, геодезическая кривизна

Основная статья: Геодезическая

Кривая на поверхности называется геодезической линией, или просто геодезической, если во всех её точках главная нормаль к кривой совпадает с нормалью к поверхности. Пример: на плоскости геодезическими будут прямые и отрезки прямых, на сфере — большие круги и их отрезки.

Эквивалентное определение: у геодезической линии проекция её главной нормали на касательную плоскость есть нулевой вектор. Если кривая не является геодезической, то указанная проекция ненулевая; её длина называется геодезической кривизной [math]\displaystyle{ k_g }[/math] кривой на поверхности. Имеет место соотношение:

[math]\displaystyle{ k^2 = k_g^2 + k_n^2 }[/math],

где [math]\displaystyle{ k }[/math] — кривизна данной кривой, [math]\displaystyle{ k_n }[/math] — кривизна нормального сечения поверхности с той же касательной.

Геодезические линии относятся к внутренней геометрии. Перечислим их главные свойства.

• Через данную точку поверхности в заданном направлении проходит одна и только одна геодезическая.
• На достаточно малом участке поверхности две точки всегда можно соединить геодезической, и притом только одной. Пояснение: на сфере противоположные полюса соединяет бесконечное количество меридианов, а две близкие точки можно соединить не только отрезком большого круга, но и его дополнением до полной окружности, так что однозначность соблюдается только в малом.
• Геодезическая является кратчайшей. Более строго: на малом куске поверхности кратчайший путь между заданными точками лежит по геодезической.

Площадь

Ещё один важный атрибут поверхности — её площадь, которая вычисляется по формуле:

[math]\displaystyle{ S=\iint\,|[\mathbf{r}'_u\times\mathbf{r}'_v]|\;\mathrm{d}\,u\,\mathrm{d}\,v }[/math]

Здесь [math]\displaystyle{ \mathbf{r}'_u=\left\{\frac{\partial x}{\partial u},\,\frac{\partial y}{\partial u},\,\frac{\partial z}{\partial u}\right\},\ \mathbf{r}'_v=\left\{\frac{\partial x}{\partial v},\,\frac{\partial y}{\partial v},\,\frac{\partial z}{\partial v}\right\} }[/math].

В координатах получаем:

	явное задание	параметрическое задание
выражение для площади	[math]\displaystyle{ \iint\,\sqrt{\left(\frac{\partial f}{\partial x}\right)^2+\left( \frac{\partial f}{\partial y}\right)^2+1}\;\mathrm{d}\,x\,\mathrm{d}\,y }[/math]	[math]\displaystyle{ \iint\,\sqrt{\left(\frac{D(x,y)}{D(u,v)}\right)^2+\left(\frac{D(y,z)}{D(u,v)}\right)^2+\left(\frac{D(z,x)}{D(u,v)}\right)^2}\;\mathrm{d}\,u\,\mathrm{d}\,v }[/math]

Поверхность в топологии

Ориентация

Лента Мёбиуса.

Также важной характеристикой поверхности является её ориентация.

Поверхность называется двусторонней, если на всей её протяжённости она обладает непрерывным вектором нормали. В противном случае поверхность называют односторонней.

Ориентированной называется двусторонняя поверхность с выбранным направлением нормали.

Примерами односторонних и, следовательно, неориентируемых поверхностей являются бутылка Клейна или лист Мёбиуса.

Типы поверхностей

• Замкнутая поверхность — компактная поверхность без границы.
• Открытая поверхность — полная некомпактная поверхность без границы; в случае вложенной поверхности дополнительно предполагается, что она образует замкнутое множество в объемлющем пространстве.
• ориентируемые и неориентируемые поверхности

Примеры

Поверхность вращения, полученная путём вращения кривой [math]\displaystyle{ x = 2 + \cos z }[/math] вокруг оси z.

Поверхности вращения

Подробнее см. Поверхность вращения

Поверхность вращения может быть получена вращением кривой в плоскости xz вокруг оси z в предположении, что кривая не пересекает ось z. Предположим, что кривая задана выражением

[math]\displaystyle{ x= \varphi(t),\,\, z=\psi(t) }[/math]

с t лежащим в (a, b), и параметризованная длиной дуги, так что

[math]\displaystyle{ \dot{\varphi}^2 + \dot{\psi}^2 = 1. }[/math]

Тогда поверхность вращения является множеством точек

[math]\displaystyle{ M=\{(\varphi(t)\cos \theta, \varphi(t)\sin \theta,\psi(t))\colon t\in (a,b), \theta\in [0,2\pi)\}. }[/math]

Гауссова кривизна и средняя кривизна задаются выражениями

[math]\displaystyle{ K = -{\ddot{\varphi}\over \varphi},\,\, K_m = {-\dot{\psi} +\varphi(\dot{\psi}\ddot{\varphi} -\ddot{\psi}\dot{\varphi})\over 2 \varphi}. }[/math]

Эллипсоид, поверхность второго порядка

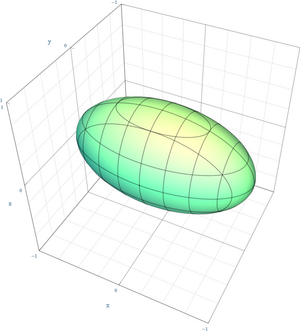
Геодезические на поверхности вращение определяются отношением Клеро.

Поверхность второго порядка

Подробнее см. Поверхность второго порядка

Рассмотрим поверхность второго порядка, заданную выражением

[math]\displaystyle{ {x^2\over a} + {y^2\over b} +{z^2\over c}=1. }[/math]

Эта поверхность позволяет параметризацию

[math]\displaystyle{ x=\sqrt{a(a-u)(a-v)\over (a-b)(a-c)},\,\, y=\sqrt{b(b-u)(b-v)\over (b-a) (b-c)}, \,\, z=\sqrt{c(c-u)(c-v)\over (c-b)(c-a)}. }[/math]

Гауссова кривизна и средняя кривизна задаются выражением

[math]\displaystyle{ K={abc\over u^2 v^2} ,\,\,K_m=-(u+v)\sqrt{abc\over u^3v^3}. }[/math]

Однолистный гиперболоид, являющийся линейчатой поверхностью в двух различных направлениях.

Линейчатые поверхности

Подробнее см. Линейчатая поверхность

Линейчатая поверхность является поверхностью, которая может быть получена движением прямой линии в [math]\displaystyle{ \mathbb{E}^3 }[/math]. Выбрав директрису на поверхности, то есть гладкую кривую единичной скорости c(t), ортогональную прямым, а затем выбрав [math]\displaystyle{ u(t) }[/math] как единичные вектора вдоль кривой в направлении прямых, для вектора скорости [math]\displaystyle{ v = c_t }[/math] и u выполняется

[math]\displaystyle{ u\cdot v=0, \,\,\|u\|=1,\,\,\|v\|=1. }[/math]

Поверхность состоит из точек

[math]\displaystyle{ c(t) + s\cdot u(t) }[/math]

при изменении s и t.

Тогда, если

[math]\displaystyle{ a=\|u_t\|, \,\, b=u_t\cdot v, \,\, \alpha=-\frac{b}{a^2}, \,\, \beta=\frac{\sqrt{a^2-b^2}}{a^2}, }[/math]

гауссова и средняя кривизна задаются выражениями

[math]\displaystyle{ K=-{\beta^2\over ((s-\alpha)^2 +\beta^2)^2} ,\,\, K_m=-{r[(s-\alpha)^2 +\beta^2)] +\beta_t(s-\alpha) + \beta\alpha_t\over [(s-\alpha)^2 +\beta^2]^{\frac32}}. }[/math]

Гауссова кривизна линейчатой поверхности обращается в нуль тогда и только тогда, когда [math]\displaystyle{ u_t }[/math] и v пропорциональны. Это условие эквивалентно тому, что поверхность является огибающей плоскостей вдоль кривой, содержащей касательный вектор v и ортогональный вектор u, то есть поверхность является развёртывающейся вдоль кривой. Более обще поверхность в [math]\displaystyle{ \mathbb{E}^3 }[/math] имеет нулевую гауссову кривизну близ точки тогда и только тогда, когда она развёртывается вблизи этой точки (Эквивалентное условие даётся ниже в терминах метрики.)

Минимальные поверхности

Подробнее см. Минимальная поверхность

В 1760 году Лагранж распространил результаты Эйлера вариационного исчисление с интегралами от одной переменной на интегралы от двух переменных. Он обдумывал следующую задачу:

Если дана замкнутая кривая в [math]\displaystyle{ \mathbb{E}^3 }[/math], находим поверхность минимальной площади, имеющая кривую в качестве границы.

Такая поверхность называется минимальной поверхностью.

В 1776 году Жан Батист Мёнье показал, что дифференциальное уравнение, полученное Лагранжем, эквивалентно обращению в нуль средней кривизны поверхности:

Поверхность минимальна тогда и только тогда, когда средняя кривизна обращается в нуль.

Минимальные поверхности имеют простую интерпретацию в реальной жизни — они имеют форму мыльной плёнки, если проволочную рамку окунуть в мыльный раствор и осторожно вынуть. Вопрос, существует ли минимальная поверхность с заданной границей, называется задачей Плато по имени бельгийского физика Жозефа Плато, который проводил эксперименты с мыльными плёнками в середине девятнадцатого века. В 1930 году Джесси Дуглас и Тибор Радо дали положительный ответ на задачу Плато (Дуглас получил одну из первых филдсовских премий за эту работу в 1936 году).

Известно много примеров минимальных поверхностей, такие как катеноид, геликоид, поверхность Шерка и поверхность Эннепера. В этой области проводились интенсивные исследования, итог которых подведён в книге Оссермана. В частности, результат Оссермана показывает, что если минимальная поверхность не планарна, то её образ при отображении Гаусса плотен в [math]\displaystyle{ S^2 }[/math].

Поверхности с постоянной отрицательной, нулевой и положительной кривизной Гаусса

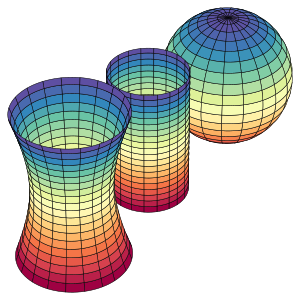
Поверхности постоянной гауссовой кривизны

Эудженио Бельтрами (1835—1899)

Если поверхность имеет постоянную гауссову кривизну, она называется поверхностью постоянной кривизны.

• Единичная сфера в [math]\displaystyle{ \mathbb{E}^3 }[/math] имеет постоянную гауссову кривизну +1.
• Евклидова плоскость и цилиндр имеют постоянную гауссову кривизну 0.
• Поверхность вращения с [math]\displaystyle{ \varphi_{tt} = \varphi }[/math] имеет постоянную гауссову кривизну −1. Частный случай получается путём принятия [math]\displaystyle{ \varphi(t) = C \mathrm{ch}\,t }[/math], [math]\displaystyle{ C \mathrm{sh}\,t }[/math] и [math]\displaystyle{ C e^t }[/math]. Последний случай является классической псевдосферой, образованной вращением трактрисы вокруг центральной оси. В 1868 году Эудженио Бельтрами показал, что геометрия псеводосферы была напрямую связана с геометрией гиперболической плоскости, открытой независимо Лобачевским (1830) и Бойяи (1832). Уже в 1840 году Ф. Майндинг, студент Гаусса, получил тригонометрические формулы для псевдосферы, идентичные формулам для гиперболической плоскости. Эта поверхность постоянной кривизны ныне лучше понимается в терминах метрики Пуанкаре на верхней полуплоскости или единичном круге и может быть описана другими моделями, такими как модель Кляйна или гиперболоидная модель, полученная рассмотрением двулистного гиперболоида [math]\displaystyle{ q(x, y, z) = -1 }[/math] в трёхмерном пространстве Минковского, где [math]\displaystyle{ q(x, y, z) = x^2 + y^2 - z^2 }[/math].

Каждая из этих поверхностей постоянной кривизны имеет транзитивную группу Ли симметрий. Этот теоретико-групповой факт имеет далеко идущие следствия, которые особенно замечательны ввиду центральной роли, которую играют эти специальные поверхности в геометрии поверхностей согласно теореме об униформизации Пуанкаре (см. ниже).

Другие примеры поверхностей с гауссовой кривизной 0 включают конусы, развёртывающиеся поверхности касательных и, более обще, любая развёртывающаяся поверхность.

Обобщение

О многомерных аналогах теории см.:

• Гиперповерхность
• Многообразие
• Подмногообразие
• Тензорный анализ

Литература

• Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
• Кудрявцев Л. Д. Курс математического анализа. — М.: Дрофа. — 570 с.
• Погорелов А. И. Дифференциальная геометрия. — 6-е издание. — М.: Наука, 1974.
• Рашевский П. К. Курс дифференциальной геометрии. — 3-е издание. — М.: ГИТТЛ, 1950.
• Поверхность // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Ссылки

• Образование поверхностей перемещением кривых, видео Архивная копия от 23 сентября 2016 на Wayback Machine