Период полураспада
Пери́од полураспа́да квантовомеханической системы (частицы, ядра, атома, энергетического уровня и т. д.) — время [math]\displaystyle{ T_{1/2} }[/math], в течение которого система распадается с вероятностью 1/2[1]. В течение одного периода полураспада в среднем вдвое уменьшается количество выживших частиц[1][2][3][4][5][6], а также интенсивность реакции распада[2][5][6].
Период полураспада наглядно характеризует скорость распада радиоактивных ядер, наряду со средним временем жизни и вероятностью распада в единицу времени (постоянной распада), эти величины связаны друг с другом простым однозначным соотношением[2][3][4][5][6].
Период полураспада является константой для данного радиоактивного ядра (изотопа). Для различных изотопов эта величина может изменяться от десятков йоктосекунд (10−24 с) у водорода-7 до более чем 1024 лет у теллура-128, что многократно превышает возраст Вселенной[4][5]. На основании постоянства периода полураспада строится метод радиоизотопного датирования[5].
Определение и основные соотношения
Понятие периода полураспада применяется как к испытывающим распад элементарным частицам, так и к радиоактивным ядрам[4]. Поскольку событие распада имеет квантовую вероятностную природу, то если рассматривать одну структурную единицу материи (частицу, атом радиоактивного изотопа), можно говорить о периоде полураспада как промежутке времени, по истечении которого средняя вероятность распада рассматриваемой частицы будет равна 1/2[1].
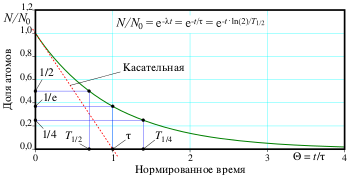
Если же рассматривать экспоненциально распадающиеся системы частиц, то периодом полураспада [math]\displaystyle{ T_{1/2} }[/math] будет называться время, в течение которого распадается в среднем половина радиоактивных ядер[1][2][3][4][5][6]. Согласно закону радиоактивного распада, число нераспавшихся атомов в момент времени [math]\displaystyle{ t }[/math] связано с начальным (в момент [math]\displaystyle{ t = 0 }[/math]) числом атомов [math]\displaystyle{ N_0 }[/math] соотношением
- [math]\displaystyle{ \frac{N(t)}{N_0} = e^{-\lambda t}, }[/math]
- где [math]\displaystyle{ \lambda }[/math] — постоянная распада[7].
По определению, [math]\displaystyle{ \frac{N(T_{1/2})}{N_0} = \frac{1}{2}, }[/math] следовательно, [math]\displaystyle{ e^{-\lambda T_{1/2}} = \frac{1}{2}, }[/math] откуда
- [math]\displaystyle{ T_{1/2} = \frac{\ln 2}{\lambda}\approx\frac{0,693}{\lambda}. }[/math]
Далее, поскольку среднее время жизни [math]\displaystyle{ \tau = \frac{1}{\lambda} }[/math], то[2][3][4][5][6]
- [math]\displaystyle{ T_{1/2} = \tau\ln 2 \approx 0,693\tau, }[/math]
то есть период полураспада примерно на 30,7 % короче, чем среднее время жизни. Например, для свободного нейтрона [math]\displaystyle{ T_{1/2} }[/math] = 10,3 минуты, а [math]\displaystyle{ \tau }[/math] = 14,9 минуты[5].
Не следует считать, что за два периода полураспада распадутся все частицы, взятые в начальный момент. Поскольку каждый период полураспада уменьшает число выживших частиц вдвое, за время [math]\displaystyle{ 2T_{1/2} }[/math] останется четверть от начального числа частиц, за [math]\displaystyle{ 3T_{1/2} }[/math] — одна восьмая и т. д.[1][5]. При этом для каждой конкретной отдельной частицы по прошествии времени [math]\displaystyle{ T_{1/2} }[/math] ожидаемая средняя продолжительность жизни (соответственно, и вероятность распада, и период полураспада) не изменится — этот контринтуитивный факт является следствием квантовой природы явления распада[1].
Парциальный период полураспада
Если система с периодом полураспада [math]\displaystyle{ T_{1/2} }[/math] может распадаться по нескольким каналам, для каждого из них можно определить парциальный период полураспада. Пусть вероятность распада по i-му каналу (коэффициент ветвления) равна [math]\displaystyle{ p_i }[/math]. Тогда парциальный период полураспада по i-му каналу равен
- [math]\displaystyle{ T_{1/2}^{(i)} = \frac{T_{1/2}}{p_i}. }[/math]
Парциальный [math]\displaystyle{ T_{1/2}^{(i)} }[/math] имеет смысл периода полураспада, который был бы у данной системы, если «выключить» все каналы распада, кроме i-го. Так как по определению [math]\displaystyle{ p_i \le 1 }[/math], то [math]\displaystyle{ T_{1/2}^{(i)} \ge T_{1/2} }[/math] для любого канала распада.
Значения для различных изотопов
Период полураспада конкретного изотопа является постоянной величиной, не зависящей от способа его получения, агрегатного состояния вещества, температуры, давления, химического состава соединения, куда оно входит, и практически любых других внешних факторов, за исключением акта прямого ядерного взаимодействия в результате, например, соударения с высокоэнергетической частицей в ускорителе[5][6].
На практике период полураспада определяют, измеряя активность исследуемого препарата через определённые промежутки времени. Учитывая, что активность препарата пропорциональна количеству атомов распадающегося вещества, и воспользовавшись законом радиоактивного распада, можно вычислить период полураспада данного вещества[8].
Значения периода полураспада для различных радиоактивных изотопов:
| Химический элемент | Обозначение | Порядковый номер (Z) | Массовое число (A) | Период полураспада |
|---|---|---|---|---|
| Актиний | Ac | 89 | 227 | 22 года[9][10] |
| Америций | Am | 95 | 243 | 7,3⋅103 лет[10][11] |
| Астат | At | 85 | 210 | 8,3 часа[9] |
| Бериллий | Be | 4 | 8 | 8,2⋅10-17 секунды[11] |
| Висмут | Bi | 83 | 208 | 3,68⋅105 лет[11][12] |
| 209 | 2⋅1019 лет[10][13] | |||
| 210 | 3,04⋅106 лет[12][13] | |||
| Берклий | Bk | 97 | 247 | 1,38⋅103 лет[10][11] |
| Углерод | C | 6 | 14 | 5730 лет[1][13] |
| Кадмий | Cd | 48 | 113 | 9⋅1015 лет[14] |
| Хлор | Cl | 17 | 36 | 3⋅105 лет[13] |
| 38 | 38 минут[13] | |||
| Кюрий | Cm | 96 | 247 | 4⋅107 лет[9] |
| Кобальт | Co | 27 | 60 | 5,27 года[13][15] |
| Цезий | Cs | 55 | 137 | 30,1 года[1][15] |
| Эйнштейний | Es | 99 | 254 | 1,3 года[9][10] |
| Фтор | F | 9 | 18 | 110 минут[11][15] |
| Железо | Fe | 26 | 59 | 45 дней[1][13] |
| Франций | Fr | 87 | 223 | 22 минуты[9][10] |
| Галлий | Ga | 31 | 68 | 68 минут[11] |
| Водород | H | 1 | 3 | 12,3 года[13][15] |
| Йод | I | 53 | 131 | 8 дней[13][15] |
| Иридий | Ir | 77 | 192 | 74 дня[13] |
| Калий | K | 19 | 40 | 1,25⋅109 лет[1][11] |
| Молибден | Mo | 42 | 99 | 66 часов[5][11] |
| Азот | N | 7 | 13 | 10 минут[13] |
| Натрий | Na | 11 | 22 | 2,6 года[13][15] |
| 24 | 15 часов[1][13][15] | |||
| Нептуний | Np | 93 | 237 | 2,1⋅106 лет[10][11] |
| Кислород | O | 8 | 15 | 124 секунды[13] |
| Фосфор | P | 15 | 32 | 14,3 дня[1][13] |
| Протактиний | Pa | 91 | 231 | 3,3⋅104 лет[11][13] |
| Полоний | Po | 84 | 210 | 138,4 дня[9][13] |
| 214 | 0,16 секунды[11] | |||
| Плутоний | Pu | 94 | 238 | 87,7 года[11] |
| 239 | 2,44⋅104 лет[1][13] | |||
| 242 | 3,3⋅105 лет[9] | |||
| Радий | Ra | 88 | 226 | 1,6⋅103 лет[9][11][10] |
| Рубидий | Rb | 37 | 82 | 76 секунд[11] |
| 87 | 49,7⋅109 лет[11] | |||
| Радон | Rn | 86 | 222 | 3,83 дня[9][13] |
| Сера | S | 16 | 35 | 87 дней[13] |
| Самарий | Sm | 62 | 147 | 1,07⋅1011 лет[11][12] |
| 148 | 6,3⋅1015 лет[11] | |||
| 149 | > 2⋅1015 лет[11][12] | |||
| Стронций | Sr | 38 | 89 | 50,5 дня[13] |
| 90 | 28,8 года[11] | |||
| Технеций | Tc | 43 | 99 | 2,1⋅105 лет[9][10] |
| Теллур | Te | 52 | 128 | 2⋅1024 лет[11] |
| Торий | Th | 90 | 232 | 1,4⋅1010 лет[9][10] |
| Уран | U | 92 | 233 | 1,⋅105 лет[13] |
| 234 | 2,5⋅105 лет[13] | |||
| 235 | 7,1⋅108 лет[1][13] | |||
| 238 | 4,5⋅109 лет[1][9][10][13] | |||
| Ксенон | Xe | 54 | 133 | 5,3 дня[13][15] |
| Иттрий | Y | 39 | 90 | 64 часа[13] |
Примеры расчётов
Пример 1
Если рассматривать достаточно близкие моменты времени [math]\displaystyle{ t_1 }[/math] и [math]\displaystyle{ t_2 }[/math], то число ядер, распавшихся за этот промежуток времени [math]\displaystyle{ t_2-t_1\ll\lambda }[/math], можно приближённо записать как [math]\displaystyle{ \Delta N\approx\lambda N_0(t_2-t_1) }[/math].
С её помощью легко оценить число атомов урана-238, имеющего период полураспада [math]\displaystyle{ T_{1/2}=4,498\cdot 10^{9} }[/math] лет, испытывающих превращение в данном количестве урана, например, в одном килограмме в течение одной секунды. Имея в виду, что количество любого элемента в граммах, численно равное атомному весу, содержит, как известно, 6,02⋅1023 атомов, а в году [math]\displaystyle{ 365\cdot 24\cdot 60\cdot 60 }[/math] секунд, можно получить, что
- [math]\displaystyle{ \Delta N\approx\frac{0,693}{4,498\cdot10^{9}\cdot365\cdot24\cdot60\cdot60} \frac{6,02\cdot10^{23}}{238} \cdot 1000 = 12\cdot10^6. }[/math]
Вычисления приводят к тому, что в одном килограмме урана в течение одной секунды распадается двенадцать миллионов атомов. Несмотря на такое огромное число, всё же скорость превращения ничтожно мала. Действительно, в секунду из наличного количества урана распадается его доля, равная
- [math]\displaystyle{ \frac{12 \cdot 10^6 \cdot 238}{6,02\cdot10^{23}\cdot1000} = 47\cdot10^{-19}. }[/math]
Пример 2
Образец содержит 10 г изотопа плутония Pu-239 с периодом полураспада 24 400 лет. Сколько атомов плутония распадается ежесекундно?
Поскольку рассматриваемое время (1 с) намного меньше периода полураспада, можно применить ту же, что и в предыдущем примере, приближённую формулу:
- [math]\displaystyle{ \Delta N \approx \Delta t \cdot N_0 \frac{\ln 2}{T_{1/2}} = \Delta t \cdot \frac{\frac{m}{\mu}N_A \ln 2}{T_{1/2}} }[/math]
Подстановка численных значений даёт [math]\displaystyle{ \Delta N \approx 1\cdot \frac{0,693 \cdot \frac{10}{239} \cdot 6\cdot 10^{23}}{24 400\cdot365\cdot24\cdot60\cdot60} = \frac{0,693 \cdot 2,5\cdot 10^{22}}{7,7\cdot 10^{11}} = 2,25\cdot 10^{10}. }[/math]
Когда рассматриваемый период времени сравним с периодом полураспада, следует пользоваться точной формулой
- [math]\displaystyle{ \Delta N = N_0 - N(t) = N_0 \left( 1-2^{-t/T_{1/2}} \right). }[/math]
Она пригодна в любом случае, однако для малых периодов времени требует вычислений с очень большой точностью. Так, для данной задачи:
- [math]\displaystyle{ \Delta N = N_0 \left( 1-2^{-t/T_{1/2}} \right) = 2.5\cdot 10^{22} \left( 1-2^{-1/7.7 \cdot 10^{11}} \right) = 2.5\cdot 10^{22} \left( 1-0.99999999999910 \right) = 2.25\cdot 10^{10}. }[/math]
Стабильность периода полураспада
Во всех наблюдавшихся случаях (кроме некоторых изотопов, распадающихся путём электронного захвата) период полураспада был постоянным (отдельные сообщения об изменении периода были вызваны недостаточной точностью эксперимента, в частности, неполной очисткой от высокоактивных изотопов). В связи с этим период полураспада считается неизменным. На этом основании строится определение абсолютного геологического возраста горных пород, а также радиоуглеродный метод определения возраста биологических останков: зная концентрацию радиоизотопа в настоящее время и в прошлом, можно рассчитать, сколько точно времени прошло с тех пор[5].
Предположение об изменяемости периода полураспада используется креационистами, а также представителями т. н. «альтернативной науки» для опровержения научной датировки горных пород, остатков живых существ и исторических находок, с целью дальнейшего опровержения научных теорий, построенных с использованием такой датировки. (См., например, статьи Креационизм, Научный креационизм, Критика эволюционизма, Туринская плащаница).
Вариабельность постоянной распада для электронного захвата наблюдалась в эксперименте, но она лежит в пределах процента во всём доступном в лаборатории диапазоне давлений и температур. Период полураспада в этом случае изменяется в связи с некоторой (довольно слабой) зависимостью плотности волновой функции орбитальных электронов в окрестности ядра от давления и температуры. Существенные изменения постоянной распада наблюдались также для сильно ионизованных атомов (так, в предельном случае полностью ионизованного ядра электронный захват может происходить только при взаимодействии ядра со свободными электронами плазмы; кроме того, распад, разрешённый для нейтральных атомов, в некоторых случаях для сильно ионизованных атомов может быть запрещён кинематически). Все эти варианты изменения постоянных распада, очевидно, не могут быть привлечены для «опровержения» радиохронологических датировок, поскольку погрешность самого радиохронометрического метода для большинства изотопов-хронометров составляет более процента, а высокоионизованные атомы в природных объектах на Земле не могут существовать сколько-нибудь длительное время.
Поиск возможных вариаций периодов полураспада радиоактивных изотопов, как в настоящее время, так и в течение миллиардов лет, интересен в связи с гипотезой о вариациях значений фундаментальных констант в физике (постоянной тонкой структуры, константы Ферми и т. д.). Однако тщательные измерения пока не принесли результата — в пределах погрешности эксперимента изменения периодов полураспада не были найдены. Так, было показано, что за 4,6 млрд лет константа α-распада самария-147 изменилась не более чем на 0,75 %, а для β-распада рения-187 изменение за это же время не превышает 0,5 %[16]; в обоих случаях результаты совместимы с отсутствием таких изменений вообще.
См. также
Примечания
- ↑ Перейти обратно: 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 Richard A. Muller. Physics and Technology for Future Presidents : An Introduction to the Essential Physics Every World Leader Needs to Know : [англ.]. — Princeton, New Jercey : Princeton University Press, 2010. — С. 128—129. — 526 с. — ISBN 978-0-691-13504-5.
- ↑ Перейти обратно: 2,0 2,1 2,2 2,3 2,4 Климов А. Н. Глава 3. Ядерные превращения // Ядерная физика и ядерные реакторы. — М.: Энергоатомиздат, 1985. — С. 74—75. — 352 с.
- ↑ Перейти обратно: 3,0 3,1 3,2 3,3 Период полураспада. Энциклопедия физики и техники. Дата обращения: 18 ноября 2019. Архивировано 4 декабря 2019 года.
- ↑ Перейти обратно: 4,0 4,1 4,2 4,3 4,4 4,5 Б.С. Ишханов, И.М. Капитонов, Э.И. Кэбин. Период полураспада. Частицы и атомные ядра. Основные понятия. Кафедра общей ядерной физики физического факультета МГУ. Дата обращения: 18 ноября 2019. Архивировано 6 ноября 2019 года.
- ↑ Перейти обратно: 5,00 5,01 5,02 5,03 5,04 5,05 5,06 5,07 5,08 5,09 5,10 5,11 Carl R. (Rod) Nave. Radioactive Half-Life. HyperPhysics. Georgia State University (2016). Дата обращения: 22 ноября 2019. Архивировано 27 сентября 2017 года.
- ↑ Перейти обратно: 6,0 6,1 6,2 6,3 6,4 6,5 Б.С. Ишханов, И.М. Капитонов, Н.П. Юдин. Радиоактивность // Частицы и атомные ядра. — 2-е. — М. : Издательство ЛКИ. — Гл. 1. Элементарные частицы. — С. 18—21. — 584 с. — (Классический университетский учебник). — ISBN 978-5-382-00060-2.
- ↑ Такой же вид имеет зависимость от времени интенсивности (скорости) распада, то есть активности образца, и аналогичным образом через неё определяется период полураспада как промежуток времени, по истечении которого интенсивность распада снизится вдвое
- ↑ Фиалков Ю. Я. Применение изотопов в химии и химической промышленности. — К.: Техніка, 1975. — С. 52. — 240 с. — 2000 экз.
- ↑ Перейти обратно: 9,00 9,01 9,02 9,03 9,04 9,05 9,06 9,07 9,08 9,09 9,10 9,11 Период полураспада радиоактивных элементов и их излучение (Таблица). infotables.ru - Справочные таблицы. Дата обращения: 6 ноября 2019. Архивировано 6 ноября 2019 года.
- ↑ Перейти обратно: 10,00 10,01 10,02 10,03 10,04 10,05 10,06 10,07 10,08 10,09 10,10 Half Life for all the elements in the Periodic Table. periodictable.com. Дата обращения: 11 ноября 2019. Архивировано 24 марта 2019 года.
- ↑ Перейти обратно: 11,00 11,01 11,02 11,03 11,04 11,05 11,06 11,07 11,08 11,09 11,10 11,11 11,12 11,13 11,14 11,15 11,16 11,17 11,18 11,19 Kondev F. G., Wang M., Huang W. J., Naimi S., Audi G. The Nubase2020 evaluation of nuclear properties (англ.) // Chinese Physics C. — 2021. — Vol. 45, iss. 3. — P. 030001-1—030001-180. — doi:10.1088/1674-1137/abddae.
- ↑ Перейти обратно: 12,0 12,1 12,2 12,3 Radioactive isotope table. Caltech Astronomy Department. Дата обращения: 10 ноября 2019. Архивировано 31 октября 2019 года.
- ↑ Перейти обратно: 13,00 13,01 13,02 13,03 13,04 13,05 13,06 13,07 13,08 13,09 13,10 13,11 13,12 13,13 13,14 13,15 13,16 13,17 13,18 13,19 13,20 13,21 13,22 13,23 13,24 13,25 13,26 Период полураспада Т1/2 некоторых радиоактивных изотопов (выборочно), калькулятор онлайн, конвертер. Калькулятор – справочный портал. Дата обращения: 7 ноября 2019. Архивировано 7 ноября 2019 года.
- ↑ Рекорды в науке и технике. Элементы. МОО "Наука и техника". Дата обращения: 7 ноября 2019. Архивировано 7 ноября 2019 года.
- ↑ Перейти обратно: 15,0 15,1 15,2 15,3 15,4 15,5 15,6 15,7 M. P. Unterweger, D. D. Hoppes, F. J. Schima, and J. S. Coursey. Radionuclide Half-Life Measurements Data (англ.). NIST (6 сентября 2009). Дата обращения: 26 ноября 2019. Архивировано 3 февраля 2020 года.
- ↑ Jean-Philippe Uzan. The fundamental constants and their variation: observational status and theoretical motivations. Rev.Mod.Phys. 75(2003)403. arXiv: hep-ph/0205340 Архивная копия от 3 июня 2015 на Wayback Machine.
