Узел (математика)
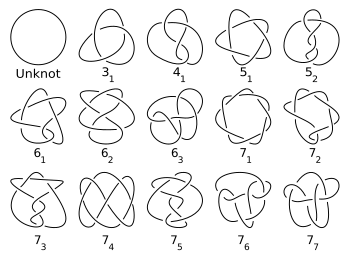



У́зел в математике — вложение окружности (одномерной сферы) в трёхмерное евклидово пространство, рассматриваемое с точностью до изотопии. Основной предмет изучения теории узлов. Два узла топологически эквивалентны, если один из них можно продеформировать в другой, причём в процессе деформации не должно возникать самопересечений.
Частным случаем является вопрос о распознавании тривиальности того или иного узла, то есть о том, является ли заданный узел изотопным тривиальному узлу (можно ли его развязать).
Для определения того, является ли конкретный узел тривиальным, можно использовать различные инварианты узлов, например многочлен Александера или фундаментальную группу дополнения. Обычно их можно посчитать исходя из узловой диаграммы.
В топологии рассматриваются узлы только на замкнутых линиях потому, что не замкнутые можно развязать[1].
Определение
Узел - гладкое подмногообразие трехмерной сферы [math]\displaystyle{ S^{3}, }[/math] гомеоморфное [math]\displaystyle{ S^{1}. }[/math] Под [math]\displaystyle{ S^{3} }[/math] понимается ориентированная трехмерная сфера, а ориентация окружности [math]\displaystyle{ S^{1} }[/math] обычно несущественна.
Узел [math]\displaystyle{ Y }[/math] называется срезанным, если существует двухмерный диск [math]\displaystyle{ D\subset B^{4}, }[/math] что [math]\displaystyle{ Y=\partial D }[/math] (см. Граница (топология) и Расслоение на окружности).
Узлы [math]\displaystyle{ Y_{1},Y_{2} }[/math] являются кобордантными, если существует гладко вложенное в [math]\displaystyle{ S^{3}\times I }[/math] кольцо, которое пересекает [math]\displaystyle{ S\times\{t\} }[/math] по [math]\displaystyle{ Y_{t} }[/math] ([math]\displaystyle{ t=0,1 }[/math]) (см. Семейство (математика)). Группа кобордизмов узлов [math]\displaystyle{ K^{3}_{1} }[/math] - кобордантные ориентированные узлы с операцией связного суммирования. Рассмотрим [math]\displaystyle{ K^{n+2}_{n} }[/math] сферы в сфере [math]\displaystyle{ S^{n+2}. }[/math] Если [math]\displaystyle{ n }[/math] четно, то [math]\displaystyle{ K^{n+2}_{n}=0. }[/math]
Связка
Понятия косы и узла обобщаются понятием связки. Связка с [math]\displaystyle{ k }[/math] входами и [math]\displaystyle{ l }[/math] выходами (то есть, [math]\displaystyle{ (k,l) }[/math]-связка) - система непересекающихся дуг и окружностей, гладко вложенных в полосу [math]\displaystyle{ \mathbb{R}^{2}\times[0,1], }[/math] такая, что концы дуг есть точками [math]\displaystyle{ (1,0,0),\,(2,0,0),\,...,(k,0,0) }[/math] и [math]\displaystyle{ (1,0,1),\,(2,0,1),\,...,(l,0,1); }[/math] окружности лежат в [math]\displaystyle{ \mathbb{R}^{2}\times (0,1). }[/math] Эти дуги и окружности в [math]\displaystyle{ \mathbb{R}^{2}\times[0,1] }[/math] называются компонентами связки[2].
Классификация
Трилистник, узел [math]\displaystyle{ 3_1 }[/math] является первым нетривиальным узлом и единственным узлом с числом пересечений три. Он является простым и перечислен с под номером 31 в нотации Александера-Бриггса. Нотация Даукера[англ.] для трилистника — 4 6 2, а нотация Конвея трилистника — [3].
Трилистник нетривиален, что означает, что невозможно «развязать» трилистник в трёхмерном пространстве без разрезания. С математической точки зрения это означает, что трилистник не изотопен тривиальному узлу. В частности, не существует последовательности движений Рейдемейстера, с помощью которых узел развязывается.
Восьмёрка, четырёхкратный узел или узел Листинга, узел [math]\displaystyle{ 4_1 }[/math] ― один из простейших нетривиальных узлов. Восьмёрка обозначается символом [math]\displaystyle{ 4_1 }[/math]. Впервые рассмотрен Листингом, учеником Гаусса, в 1847 году.
Трилистник хирален в том смысле, что трилистник отличается от своего собственного зеркального отражения. Два варианта трилистника известны как левосторонний и правосторонний. Невозможно путём деформации левосторонний вариант непрерывным образом перевести в правосторонний или наоборот. (То есть, эти два трилистника не изотопны.)
Также, можно показать, что трилистник (как правый, так и левый) неизотопен восьмёрке.
Пятилистник, известный также как узел [math]\displaystyle{ 5_1 }[/math] в обозначениях Александера и Бриггса, узел «Лапчатка» и печать Соломона, — это узел, для которого число пересечений (минимальное возможное число самопересечений на диаграмме — плоском рисунке — узла) равно пяти.
Для многокомпонентных узлов в верхнем индексе указывается количество компонентов: например, зацепление двух колец имеет символическую запись [math]\displaystyle{ 2^2_1 }[/math].
Это были примеры полиномиальных[3] узлов. Неполиномиальным узлом является дикий узел[4]

Ди́кий у́зел — узел [math]\displaystyle{ L }[/math] в евклидовом пространстве [math]\displaystyle{ E^3 }[/math] такой, что не существует гомеоморфизма [math]\displaystyle{ E^3 }[/math] на себя, при котором [math]\displaystyle{ L }[/math] переходит в замкнутую ломаную, состоящую из конечного числа отрезков.
Узлы и зацепления
Вложение (чаще — его образ) несвязной суммы [math]\displaystyle{ \mu }[/math] экземпляров окружности в [math]\displaystyle{ \mathbb{R}^3 }[/math] или [math]\displaystyle{ S^3 }[/math] называется зацеплением кратности [math]\displaystyle{ \mu }[/math].
Зацепление кратности [math]\displaystyle{ \mu=1 }[/math] называется узлом.
Узлы, составляющие данное зацепление, называются его компонентами.
Инварианты узлов
В теории узлов число пересечений узла — это наименьшее число пересечений на любой диаграмме узла. Число пересечений является инвариантом узла.
Например, тривиальный узел имеет нулевое число пересечений, число пересечений трилистника равно трём, а число пересечений восьмёрки равно четырём.
Дополнение узла
Теорема Гордона — Люкке[англ.] утверждает, что дополнение узла (как топологического пространства) является «полным инвариантом» узла, в том смысле, что он отличает заданный узел от всех остальных с точностью до объемлющей изотопии и зеркального отражения. Среди инвариантов, связанных с дополнением узла, есть группа узла, которая является просто фундаментальной группой его дополнения.
Примечания
- ↑ Болтянский В.Г., Ефремович В.А. Наглядная топология. — М.: Наука, 1983. Серия Библиотечка «Квант», выпуск 21. — С.87
- ↑ Кассел К., Россо М., Тураев В. - Квантовые группы и инварианты узлов. - Москва: Институт компьютерных исследований, 2002, 140 стр.
- ↑ Armstrong (1983), p. 215.
- ↑ Livingstone (1996), Section 2.1 Wild Knots and Unknottings, pp. 11-14.
Литература
- Simon Jonathan. Mathematical Approaches to Biomolecular Structure and Dynamics / Jill P. Mesirov, Klaus Schulten, De Witt Sumners. — 1996. — Т. 82. — (The IMA Volumes in Mathematics and its Applications). — doi:10.1007/978-1-4612-4066-2_4.
- P.G. Tait. Scientific papers. — Cambridge University Press, 1898. — Т. 1.
- C. A. Adams. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. — American Mathematical Society, 2004. — ISBN 9780821836781.
- Кроуэлл Р., Фокс Р. Введение в теорию узлов / Пер. с англ. — Череповец: Меркурий-Пресс, 2000. — 348 с. — ISBN 5-1148-0112-0..
- Мантуров В. О. Теория узлов. — М.: РХД, 2005. — 512 с. — ISBN 5-93972-404-3..
- Мантуров В. О. Лекции по теории узлов и их инвариантов. — М.: Едиториал УРСС, 2001. — 204 с. — ISBN 5-8360-0287-8..
- Милнор Дж. Особые точки комплексных гиперповерхностей / Пер. с англ. — М.: Мир, 1971. — 127 с.
- Мандельбаум Р. Четырёхмерная топология / Пер. с англ. — М.: Мир, 1981. — 286 с.
- Hillman J. A. Alexander ideals of links B. — Hdlb. — N. Y., 1981.
- Джонс, Воган Ф. Р. Теория узлов и статистическая механика // Scientific American (издание на русском языке). — № 1. — 1991. — С. 44—50.
- Сосинский, А. Б. Узлы и косы. — М.: МЦНМО, 2001. — Т. 10. — 24 с. — (Библиотека «Математическое просвещение»). — ISBN 5-900916-76-6..
- Статьи «Теория узлов в конце XX века» // Математическое просвещение. — № 3. — 1999.
- Мантуров В. О. Экскурс в теорию узлов // Сетевой образовательный журнал. — 2004. — Т. 8, № 1. — С. 122—127.
- H. Gruber. Estimates for the minimal crossing number. — 2003. — arXiv:math/0303273.
- Yuanan Diao. The additivity of crossing numbers // Journal of Knot Theory and its Ramifications. — 2004. — Т. 13, вып. 7. — doi:10.1142/S0218216504003524.
- Marc Lackenby. The crossing number of composite knots // Journal of Topology. — 2009. — Т. 2, вып. 4. — doi:10.1112/jtopol/jtp028.
- Honda K. 3-dimensional methods in contact geometry. (англ.)
- Etnyre J. B. Legendrian and Transversal Knots. (англ.)
- Birman J.S. Braids, knots and contact structures. (англ.)
- Weisstein, Eric W. Knot Theory (англ.) на сайте Wolfram MathWorld.