Соотношение Бретшнайдера

Соотношение Бретшнайдера — соотношение в четырёхугольнике, аналог теоремы косинусов.

Формулировка

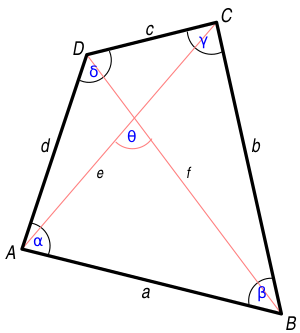
Между сторонами a, b, c, d, углами [math]\displaystyle{ \alpha, \gamma, }[/math] противоположными друг другу, и диагоналями e, f простого (несамопересекающегося) четырёхугольника выполняется соотношение:

[math]\displaystyle{ e^2f^2=a^2c^2+b^2d^2-2abcd\cos(\alpha + \gamma). }[/math]

Замечание

Эквивалентные формулировки:
[math]\displaystyle{ e^2f^2=(ac+bd)^2-4abcd\cos^2 \frac{\alpha + \gamma}{2}, }[/math]

[math]\displaystyle{ e^2f^2=(ac-bd)^2+4abcd\sin^2\frac{\alpha + \gamma}{2}. }[/math]

Доказательство

Вне четырёхугольника построим внешним образом [math]\displaystyle{ \triangle ABF }[/math] подобный [math]\displaystyle{ \triangle CAD }[/math] и [math]\displaystyle{ \triangle ADE }[/math] подобный [math]\displaystyle{ \triangle CAB }[/math], чтобы

[math]\displaystyle{ \angle CAD = \angle FBA }[/math],

[math]\displaystyle{ \angle ACD = \angle FAB }[/math],

[math]\displaystyle{ \angle BAC = \angle ADE }[/math],

[math]\displaystyle{ \angle BCA = \angle DAE }[/math].

Из свойства подобных треугольников имеем: [math]\displaystyle{ \frac{AF}{a} = \frac{c}{e} }[/math]; [math]\displaystyle{ \frac{BF}{a} = \frac{d}{e} }[/math]; [math]\displaystyle{ \frac{AE}{d} = \frac{b}{e} }[/math]; [math]\displaystyle{ \frac{DE}{d} = \frac{a}{e} }[/math]. Отсюда [math]\displaystyle{ AF = \frac{ac}{e} }[/math]; [math]\displaystyle{ AE = \frac{bd}{e} }[/math]; [math]\displaystyle{ BF = DE = \frac{ad}{e} }[/math]. Сумма углов [math]\displaystyle{ \angle B }[/math] и [math]\displaystyle{ \angle D }[/math] в четырёхугольнике [math]\displaystyle{ FBDE }[/math] равна сумме углов [math]\displaystyle{ \triangle BAD }[/math], то есть равна [math]\displaystyle{ 180^\circ }[/math]. Отсюда [math]\displaystyle{ FB \parallel DE }[/math]. Также [math]\displaystyle{ FB = DE }[/math], то есть [math]\displaystyle{ FBDE }[/math] — параллелограмм. Отсюда [math]\displaystyle{ f = BD = FE }[/math]. В [math]\displaystyle{ \triangle AEF }[/math] угол [math]\displaystyle{ \angle EAF = \angle A + \angle C }[/math] по построению. По теореме косинусов: [math]\displaystyle{ f^2 = \left(\frac{ac}{e}\right)^2 + \left(\frac{bd}{e}\right)^2 - \frac{2abcd}{e^2} \cos(\angle A + \angle C) }[/math]. Умножением на [math]\displaystyle{ e^2 }[/math] получаем требуемое:[math]\displaystyle{ (ef)^2 = (ac)^2 + (bd)^2 - 2abcd \cos(\angle A + \angle C) }[/math], ч. т. д.

Следствия

Если четырёхугольник вырождается в треугольник (одна вершина попадает на сторону), то получается теорема Стюарта.
Если четырёхугольник вырождается в треугольник и одна вершина попадает на середину стороны, то с учётом равенства основного угла и дополнительного также получается Теорема Аполлония.
Если четырёхугольник вписан в окружность, то [math]\displaystyle{ \frac{\alpha + \gamma}{2}=\frac{\pi}{2} }[/math]. Тогда из предпоследней формулы выше следует первая теорема Птолемея: [math]\displaystyle{ ef=ac+bd }[/math].
Если D — центр описанной окружности треугольника ABC, то DA = DB = DC. Используя теорему об углах вписанных в окружность, получим теорему косинусов для треугольника ABC.

См. также

Литература

Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 85—86. — ISBN 5-94057-170-0.