Теорема косинусов
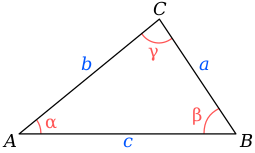
Теорема косинусов — теорема евклидовой геометрии, обобщающая теорему Пифагора на произвольные плоские треугольники.
Формулировка
Для плоского треугольника со сторонами [math]\displaystyle{ a, b, c }[/math] и углом [math]\displaystyle{ \alpha }[/math], противолежащим стороне [math]\displaystyle{ a }[/math], справедливо соотношение:
- [math]\displaystyle{ a^2 = b^2 + c^2 -2\cdot b \cdot c \cdot \cos \alpha }[/math].
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними[1]
Доказательства
Следствия
- Теорема косинусов может быть использована для нахождения косинуса угла треугольника
- [math]\displaystyle{ \cos{\alpha} = \frac{b^2 + c^2 - a^2}{2bc} }[/math]
- В частности,
- Если [math]\displaystyle{ b^2 + c^2 - a^2 \gt 0 }[/math], угол α — острый
- Если [math]\displaystyle{ b^2 + c^2 - a^2 = 0 }[/math], угол α — прямой (если угол α прямой, то теорема косинусов становится теоремой Пифагора)
- Если [math]\displaystyle{ b^2 + c^2 - a^2 \lt 0 }[/math], угол α — тупой
- Теорема косинусов может быть записана также в следующем виде[2]:
- [math]\displaystyle{ a^2 = (b + c)^2 - 4\cdot b \cdot c \cdot \cos^2 (\alpha/2) }[/math],
- [math]\displaystyle{ a^2 = (b - c)^2 + 4\cdot b \cdot c \cdot \sin^2 (\alpha/2) }[/math].
- Находя из двух последних формул в явном виде [math]\displaystyle{ \cos (\alpha/2) }[/math] и [math]\displaystyle{ \sin (\alpha/2) }[/math], получим известные формулы геометрии[2]:
- [math]\displaystyle{ \cos \frac{\alpha}{2}= \sqrt{\frac{p(p-a)}{bc}} }[/math], [math]\displaystyle{ \sin \frac{\alpha}{2}= \sqrt{\frac{(p-b)(p-c)}{bc}} }[/math], [math]\displaystyle{ \operatorname{tg} \frac{\alpha}{2} = \sqrt{\frac{(p-b)(p-c)}{p(p-a)}} }[/math], где p — полупериметр.
- Наконец, используя правые части формул для [math]\displaystyle{ \cos (\alpha/2) }[/math] и [math]\displaystyle{ \sin (\alpha/2) }[/math] и известную формулу площади треугольника: [math]\displaystyle{ S_{\triangle ABC}=\frac {1}{2} bc \sin \alpha }[/math], а также известную формулу синуса двойного угла [math]\displaystyle{ \sin \alpha = 2 \sin (\alpha/2) \cos (\alpha/2) }[/math] после небольших преобразований получим известную формулу Герона для площади треугольника: [math]\displaystyle{ S_{\triangle ABC}= \sqrt{p(p-a)(p-b)(p-c)} }[/math], где p — полупериметр.
Для других углов
Теорема косинусов для двух других углов имеет вид:
- [math]\displaystyle{ c^2\ = a^2 + b^2 - 2ab\cos\gamma }[/math]
- [math]\displaystyle{ b^2\ = a^2 + c^2 - 2ac\cos\beta }[/math]
Из этих и из основной формулы могут быть выражены углы:
- [math]\displaystyle{ \alpha=\arccos\left(\frac{b^2+c^2-a^2}{2bc}\right) }[/math]
- [math]\displaystyle{ \beta=\arccos\left(\frac{a^2+c^2-b^2}{2ac}\right) }[/math]
- [math]\displaystyle{ \gamma=\arccos\left(\frac{a^2+b^2-c^2}{2ab}\right) }[/math]
История
Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» Евклида.
Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях ал-Баттани.[3]:105 Теорему косинусов для сферического треугольника в привычном нам виде сформулировал Региомонтан, назвав её «теоремой Альбатегния» по имени ал-Баттани.
В Европе теорему косинусов популяризовал Франсуа Виет в XVI столетии. В начале XIX столетия её стали записывать в принятых по сей день алгебраических обозначениях.
Вариации и обобщения
- Теоремы косинусов (сферическая геометрия) или Теорема косинусов для трёхгранного угла.
- Теоремы косинусов (геометрия Лобачевского)
- Тождество параллелограмма. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон (см. также Теорема Птолемея):
- [math]\displaystyle{ AC^2+BD^2 = AB^2 + BC^2 + CD^2 + DA^2. }[/math]
Для евклидовых нормированных пространств
Пусть в евклидовом пространстве [math]\displaystyle{ E }[/math] задана норма, ассоциированная со скалярным произведением, то есть [math]\displaystyle{ \left\Vert \vec{a} \right\Vert = \sqrt{(\vec{a}, \vec{a})} }[/math]. Тогда теорема косинусов формулируется следующим образом:
|
Теорема. |
Для четырёхугольников
Возводя в квадрат тождество [math]\displaystyle{ \overline{AD}=\overline{AB}+\overline{BC}+\overline{CD} }[/math] можно получить утверждение, иногда называемое теоремой косинусов для четырёхугольников:
- [math]\displaystyle{ d^2=a^2+b^2+c^2-2ab\cos\angle B-2ac\cos\omega-2bc\cos\angle C }[/math], где [math]\displaystyle{ \omega }[/math] — угол между прямыми AB и CD.
Или иначе:
- [math]\displaystyle{ d^2=a^2+b^2+c^2-2ab\cos\angle B+2ac\cos(\angle A+\angle D)-2bc\cos\angle C }[/math]
- Формула справедлива и для тетраэдра, под [math]\displaystyle{ w }[/math] подразумевается угол между скрещивающимися ребрами.
- С помощью неё можно найти косинус угла между скрещивающимися ребрами [math]\displaystyle{ a }[/math] и [math]\displaystyle{ c }[/math] зная все ребра тетраэдра:
- [math]\displaystyle{ \cos w =(b^2+d^2-e^2-f^2)/2ac }[/math]
- Где [math]\displaystyle{ b }[/math] и [math]\displaystyle{ d }[/math], [math]\displaystyle{ e }[/math] и [math]\displaystyle{ f }[/math] пары скрещивающихся ребер тетраэдра.
Косвенный аналог для четырёхугольника
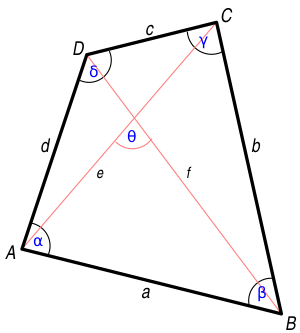
Соотношение Бретшнайдера — соотношение в четырёхугольнике, косвенный аналог теоремы косинусов:
|
- Если четырёхугольник вырождается в треугольник, и одна вершина попадает на сторону, то получается теорема Стюарта.
- Теорема косинусов для треугольника является частным случаем соотношения Бретшнайдера, если в качестве четвёртой вершины выбрать центр описанной окружности треугольника.
Симплексы
- [math]\displaystyle{ S_i S_j \cos\angle A = \frac{(-1)^{(n-1+i+j)}}{2^{n-1} ((n-1)!)^2} \begin{vmatrix} 0 & 1 & 1 & 1 & \dots & 1 \\ 1 & 0 & d_{12}^2 & d_{13}^2 & \dots & d_{1(n+1)}^2 \\ 1 & d_{21}^2 & 0 & d_{23}^2 & \dots & d_{2(n+1)}^2 \\ 1 & d_{31}^2 & d_{32}^2 & 0 & \dots & d_{3(n+1)}^2 \\ \vdots&\vdots&\vdots & \vdots & \ddots& \vdots \\ 1 & d_{(n+1)1}^2 & d_{(n+1)2}^2 & d_{(n+1)3}^2 & \dots & 0 \\ \end{vmatrix} }[/math]
при этом мы должны зачеркнуть строку и столбец, где находится [math]\displaystyle{ d_{ij} }[/math] или [math]\displaystyle{ d_{ji} }[/math].
A — угол между гранями [math]\displaystyle{ S_i }[/math] и [math]\displaystyle{ S_j }[/math], [math]\displaystyle{ S_i }[/math] -грань, находящаяся против вершины i,[math]\displaystyle{ d_{ij} }[/math]- расстояние между вершинами i и j.
См. также
- Решение треугольников
- Скалярное произведение
- Соотношение Бретшнайдера
- Теорема косинусов для трёхгранного угла
- Теорема о проекциях
- Теорема Пифагора
- Сферическая теорема косинусов
- Теорема котангенсов
- Теорема синусов
- Теорема тангенсов
- Тригонометрические тождества
- Тригонометрические функции
Примечания
- ↑ Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 7—9: учеб. для общеобразоват. учреждений — 15-е изд. — М.: Просвещение, 2005. — С. 257. — 384 с.: ил. — ISBN 5-09-014398-6
- ↑ Перейти обратно: 2,0 2,1 Корн Г. А., Корн Т. М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — С. 51. — 832 с.
- ↑ Florian Cajori. A History of Mathematics — 5th edition 1991
Литература
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 84—85. — ISBN 5-94057-170-0.
Для улучшения этой статьи по математике желательно: |
