Гиперболический треугольник
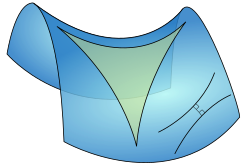
В гиперболической геометрии гиперболический треугольник является треугольником на гиперболической плоскости. Он состоит из трёх отрезков, называемых сторонами или рёбрами, и трёх точек, называемых углами или вершинами.
Как и в евклидовом случае, три точки гиперболического пространства произвольной размерности всегда лежат в той же плоскости. Следовательно, планарные гиперболические треугольники также описывают треугольники, возможные в любых гиперболических пространствах высокой размерности.
Определение
Гиперболический треугольник состоит из трёх неколлинеарных точек и трёх отрезков между ними[1].
Свойства
Гиперболические треугольники имеют некоторые свойства, которые аналогичны свойствам треугольников в евклидовой геометрии:
- Каждый гиперболический треугольник имеет вписанную окружность, но не любой гиперболический треугольник имеет описанную окружность (см. ниже)[2][3]. Его вершины могут лежать на орицикле или гиперцикле.
Гиперболические треугольники имеют некоторые свойства, аналогичные свойствам треугольников на сферической или эллиптической геометрии:
- Два треугольника с той же суммой углов равны по площади.
- Существует верхняя граница для площади треугольников.
- Существует верхняя граница для радиуса вписанной окружности.
- Два треугольника конгруэнтны тогда и только тогда, когда они переходят друг в друга в результате конечного числа отражений относительно прямой.
- Два треугольника с равными соответствующими углами конгруэнтны (то есть все подобные треугольники конгруэнтны).
Гиперболические треугольники имеют некоторые свойства, которые противоположны свойствам треугольников в сферической или эллиптической геометрии:
- Сумма углов треугольника меньше 180°.
- Площадь треугольника пропорциональна дефициту его суммы углов (до 180°).
Гиперболические треугольники имеют также некоторые свойства, которых нет в других геометриях:
- Некоторые гиперболические треугольники не имеют описанной окружности, что бывает в случае, когда по меньшей мере одна из вершин является идеальной точкой или когда все из вершин лежат на орицикле или на одностороннем гиперцикле.
- Гиперболические треугольники тонкие, существует максимальное расстояние δ от точки на стороне до других двух сторон. Этот принцип приводит к появлению δ-гиперболических пространств.
Треугольники с идеальными вершинами

Определение треугольника можно обобщить, если разрешить вершинам лежать на идеальной границе гиперплоскости, при этом стороны должны лежать внутри плоскости. Если пара сторон является асимптотически параллельными (то есть расстояние между ними стремится к нулю при стремлении к идеальной точке, но они не пересекаются), то они заканчиваются в идеальной вершине, представленной омега-точкой.
Говорят, что такая пара сторон образует нулевой угол.
Треугольник с нулевым углом невозможен в евклидовой геометрии для прямолинейных сторон, лежащих на разных прямых. Однако такие нулевые углы возможны для касающихся окружностей[англ.].
Треугольник с одной идеальной вершиной называется омега-треугольником.
Специальные виды треугольников с идеальными вершинами:
Треугольник параллельности
Треугольник, в котором одна вершина является идеальной точкой, один угол прямой — третий угол является углом параллельности для стороны между прямым углом и третьим углом.
Треугольник Швайкерта
Треугольник, в котором две вершины являются идеальными точками, а оставшийся угол является прямым. Это один из первых гиперболических треугольников (1818), который описал Фердинанд Карл Швайкерт.
Идеальный треугольник
Треугольник, в котором все вершины являются идеальными точками. Такой треугольник является самым большим из возможных треугольников в геометрии Лобачевского, поскольку имеет нулевую сумму углов.
Стандартизованная кривизна Гаусса
Связи между углами и сторонами аналогичны связям между такими же объектами в сферической тригонометрии. Масштаб длины для сферической геометрии и геометрии Лобачевского можно, например, определить как длину стороны равностороннего треугольника с фиксированными углами.
Масштаб длины наиболее удобен, если длины измеряются в терминах абсолютной длины (специальной единицы длины, аналогичной отношению между расстояниями в сферической геометрии). Выбор масштаба длины делает формулы проще[4].
В терминах модели Пуанкаре в верхней полуплоскости абсолютная длина соответствует инфинитезимальной метрике [math]\displaystyle{ ds=\frac{|dz|}{\operatorname{Im}(z)} }[/math], а в дисковой модели Пуанкаре соответствует [math]\displaystyle{ ds=\frac{2|dz|}{1-|z|^2} }[/math]
В терминах (постоянной отрицательной) кривизны Гаусса K гиперболической плоскости единица абсолютной длины соответствует длине
- [math]\displaystyle{ R=\frac{1}{\sqrt{-K}}. }[/math]
В гиперболическом треугольнике сумма углов A, B, C (соответствующих противоположным сторонам с тем же буквами) строго меньше развёрнутого угла. Разница между мерой развёрнутого угла и суммой мер углов треугольника называется дефектом треугольника. Площадь гиперболического треугольника равна его дефекту, умноженному на квадрат R:
- [math]\displaystyle{ (\pi-A-B-C) R^2{}{}.\! }[/math]
Эта теорема, впервые доказанная Иоганном Генрихом Ламбертом[5], связана с теоремой Жирара в сферической геометрии.
Тригонометрия
Во всех формулах ниже стороны a, b и c должны быть измерены по абсолютной длине, единице, такой, что кривизна Гаусса K поверхности равна −1. Другими словами, величина R в вышестоящем параграфе должна быть принята равной 1.
Тригонометрические формулы для гиперболических треугольников зависят от гиперболических функций sh, ch, and th.
Тригонометрия прямоугольных треугольников
Если C обозначает прямой угол, то:
- Синус угла A равен гиперболическому синусу противоположной углу стороны A, делённому на гиперболический синус гипотенузы c.
- [math]\displaystyle{ \sin A=\frac{\mathrm{sh}\,a}{\,\mathrm{sh}\,c\,}.\, }[/math]
- Косинус угла A равен гиперболическому тангенсу прилежащего катета b, делённому на гиперболический тангенс гипотенузы c.
- [math]\displaystyle{ \cos A=\frac{\mathrm{th}\,b}{\,\mathrm{th}\,c\,}.\, }[/math]
- Тангенс угла A равен гиперболическому тангенсу противоположного катета a, делённого на гиперболический синус прилежащего катета b.
- [math]\displaystyle{ \mathrm{tg}\,A = \frac{\mathrm{th}\,a}{\,\mathrm{sh}\,b\,}. }[/math]
- Гиперболический косинус прилежащего катета b угла A равен косинусу угла B, делённому на синус угла A.
- [math]\displaystyle{ \textrm{ch(b)}= \frac{\cos B}{\sin A}. }[/math]
- Гиперболический косинус гипотенузы c равен произведению гиперболических косинусов катетов a и b.
- [math]\displaystyle{ \textrm{ch(c)}= \textrm{ch(a)} \textrm{ch(b)}. }[/math]
- Гиперболический косинус гипотенузы H равен произведению косинусов углов, делённому на произведение их синусов[6].
- ch(H) [math]\displaystyle{ = \frac{\cos A \cos B}{\sin A\sin B} = \mathrm{ctg}\,A \mathrm{ctg}\,B }[/math]
Отношения между углами
Верны следующие равенства[7]:
- [math]\displaystyle{ \cos A = \mathrm{ch}\,a \sin B }[/math]
- [math]\displaystyle{ \sin A = \frac{\cos B}{\mathrm{ch}\,b} }[/math]
- [math]\displaystyle{ \mathrm{tg}\,A = \frac{\cot B}{\mathrm{ch}\,c} }[/math]
- [math]\displaystyle{ \cos B = \mathrm{ch}\,b \sin A }[/math]
- [math]\displaystyle{ \mathrm{ch}\,c = \mathrm{ctg}\, A \mathrm{ctg}\, B }[/math]
Площадь
Площадь прямоугольного треугольника равна:
- Площадь [math]\displaystyle{ = \frac{\pi}{2} - \angle A - \angle B }[/math]
а также
- [math]\displaystyle{ \textrm{Area}= 2 \arctan (\mathrm{th}\,(\frac{a}{2})\mathrm{th}\,(\frac{b}{2}) ) }[/math][8].
Угол параллельности
Экземпляр омега-треугольника с прямым углом даёт конфигурацию для проверки угла параллельности в треугольнике.
В случае, когда угол B = 0, a = c = [math]\displaystyle{ \infty }[/math] и [math]\displaystyle{ \textrm{th}(\infty )= 1 }[/math], получаем [math]\displaystyle{ \cos A= \textrm{th(b)}. }[/math] (b = прилежащий катет)
Равносторонний треугольник
Тригонометрические формулы для прямоугольных треугольников дают также отношения между сторонами s и углами A равностороннего треугольника (треугольника, у которого все стороны имеют одинаковую длину и все углы равны):
[math]\displaystyle{ \cos A= \frac{\textrm{th}\frac12 s }{\textrm{th} (s)} }[/math]
[math]\displaystyle{ \mathrm{ch}\,\frac12 s= \frac{\cos(\frac12 A)}{\sin( A)}= \frac{1}{2 \sin(\frac12 A)} }[/math]
Общая тригонометрия
Независимо от того, является C прямым углом или нет, выполняются следующие соотношения: Гиперболический закон косинусов[англ.]:
- [math]\displaystyle{ \mathrm{ch}\,c=\mathrm{ch}\,a\mathrm{ch}\,b-\mathrm{sh}\,a\mathrm{sh}\,b \cos C, }[/math]
- [math]\displaystyle{ \cos C= -\cos A\cos B+\sin A\sin B \mathrm{ch}\,c, }[/math]
Существует также закон синусов:
- [math]\displaystyle{ \frac{\sin A}{\mathrm{sh}\,a} = \frac{\sin B}{\mathrm{sh}\,b} = \frac{\sin C}{\mathrm{sh}\,c}, }[/math]
и четырёхчленная формула:
- [math]\displaystyle{ \cos C\mathrm{ch}\, a=\mathrm{sh}\, a\mathrm{ch}\, b-\sin C\mathrm{ctg}\, B. }[/math]
См. также
Для гиперболической тригонометрии:
Примечания
- ↑ Stothers, 2000.
- ↑ Атанасян Л. С. Окружность // Геометрия Лобачевского / под ред. М. С. Стригуновой. — М.: БИНОМ. Лаборатория знаний, 2014. — С. 125—126. — 467 с. — ISBN 978-5-9963-2364-7.
- ↑ Атанасян Л. С. Замечательные точки и прямые треугольника // Геометрия Лобачевского / под ред. М. С. Стригуновой. — М.: БИНОМ. Лаборатория знаний, 2014. — С. 166—167. — 467 с. — ISBN 978-5-9963-2364-7.
- ↑ Needham, 1998, с. 270.
- ↑ Ratcliffe, 2006, с. 99.
- ↑ Martin, 1998, с. 433.
- ↑ Smogorzhevski, 1982, с. 63.
- ↑ Mathematics stackexchange, 2015.
Литература
- Stothers Wilson. Hyperbolic geometry. — University of Glasgow, 2000., Интерактивный сайт
- Tristan Needham. Visual Complex Analysis. — Oxford University Press, 1998. — С. 270. — ISBN 9780198534464.
- John Ratcliffe. Foundations of Hyperbolic Manifolds. — Springer, 2006. — Т. 149. — С. 99. — (Graduate Texts in Mathematics). — ISBN 9780387331973. Цитата: «То. Что площадь гиперболического треугольника пропорциональна дефекту углов, впервые появились в монографии Ламберта Theorie der Parallellinien, опубликованной в 1786»
- George E. Martin. The foundations of geometry and the non-Euclidean plane. — Corrected 4. print.. — New York, NY: Springer, 1998. — С. 433. — ISBN 0-387-90694-0.
- Smogorzhevski A.S. Lobachevskian geometry. — Moscow: Mir Publishers, 1982. — С. 63.
- Area of a right angled hyperbolic triangle as function of side lengths // Mathematics stackexchange. — 2015.
Литература для дальнейшего чтения
- Svetlana Katok (1992) Fuchsian Groups, University of Chicago Press ISBN 0-226-42583-5
Для улучшения этой статьи желательно: |