Гравитация
Гравита́ция (притяже́ние, всеми́рное тяготе́ние, тяготе́ние) (от лат. gravitas — «тяжесть») — универсальное фундаментальное взаимодействие между материальными телами, обладающими массой. В приближении малых по сравнению со скоростью света скоростей и слабого гравитационного взаимодействия описывается теорией тяготения Ньютона, в общем случае описывается общей теорией относительности Эйнштейна. В квантовом пределе гравитационное взаимодействие предположительно описывается квантовой теорией гравитации, которая ещё не разработана.
Гравитация играет крайне важную роль в структуре и эволюции Вселенной (устанавливая связь между плотностью Вселенной и скоростью её расширения)[1], определяя ключевые условия равновесия и устойчивости астрономических систем[2]. Без гравитации во Вселенной не было бы планет, звёзд, галактик, чёрных дыр[3]. Гравитационное сжатие является основным источником энергии на поздних стадиях эволюции звёзд (белые карлики, нейтронные звезды, чёрные дыры).[4]
Согласно общей теории относительности, гравитационное взаимодействие является инвариантным относительно С-симметрии, P-симметрии и Т-симметрии[5]
Гравитационное притяжение
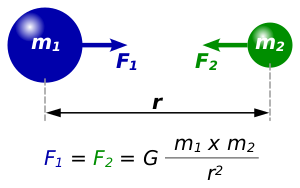
В рамках классической механики гравитационное притяжение описывается законом всемирного тяготения Ньютона, который гласит, что гравитационное притяжение между двумя материальными точками массы [math]\displaystyle{ m_1 }[/math] и [math]\displaystyle{ m_2 }[/math], разделёнными расстоянием [math]\displaystyle{ r }[/math], пропорционально обеим массам и обратно пропорционально квадрату расстояния:
- [math]\displaystyle{ F=G\frac{m_1 m_2}{r^2}. }[/math]
Здесь [math]\displaystyle{ G }[/math] — гравитационная постоянная, равная примерно 6,67⋅10−11 м³/(кг·с²)[6][7]. Этот закон выполняется в приближении при малых по сравнению со скоростью света [math]\displaystyle{ v \ll c }[/math] скоростей и слабого гравитационного взаимодействия (если для изучаемого объекта, расположенного на расстоянии [math]\displaystyle{ R }[/math] от тела массой [math]\displaystyle{ M }[/math], величина [math]\displaystyle{ \frac{GM}{c^{2}R} \ll 1 }[/math][8]). В общем случае гравитация описывается общей теорией относительности Эйнштейна.
Закон всемирного тяготения — одно из приложений закона обратных квадратов, встречающегося также и при изучении излучений (например, давление света) и являющегося прямым следствием квадратичного увеличения площади сферы при увеличении радиуса, что приводит к квадратичному же уменьшению вклада любой единичной площади в площадь всей сферы.
Гравитационное поле, так же как и поле силы тяжести, потенциально. Это значит, что работа силы притяжения не зависит от вида траектории, а только от начальной и конечной точек. Равносильно: можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не будет изменяться после перемещения тел по замкнутому контуру. Потенциальность гравитационного поля влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в гравитационном поле часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что, как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени.
Большие космические объекты — планеты, звёзды и галактики — имеют огромную массу и, следовательно, создают значительные гравитационные поля.
Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях и все массы положительны, это, тем не менее, очень важное воздействие во Вселенной. В частности, электромагнитное взаимодействие между телами в космических масштабах мало, поскольку полный электрический заряд этих тел равен нулю (вещество в целом электрически нейтрально).
Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.
Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, чёрные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.
Гравитация была первым взаимодействием, описанным математической теорией. Аристотель (IV век до н. э.) считал, что объекты с разной массой падают с разной скоростью. И только много позже (1589 год) Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687 год) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.
Небесная механика и некоторые её задачи
Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации, называется небесной механикой.
Наиболее простой задачей небесной механики является гравитационное взаимодействие двух точечных или сферических тел в пустом пространстве. Эта задача в рамках классической механики решается аналитически в замкнутой форме; результат её решения часто формулируют в виде трёх законов Кеплера.
При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе эта неустойчивость не позволяет предсказать точно движение планет на масштабах, превышающих сотню миллионов лет.
В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: Солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — сложная структура колец Сатурна.
Несмотря на попытки точно описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.
Сильные гравитационные поля
В сильных гравитационных полях (а также при движении в гравитационном поле с релятивистскими скоростями) начинают проявляться эффекты общей теории относительности (ОТО):
- изменение геометрии пространства-времени;
- как следствие, отклонение закона тяготения от ньютоновского
- и в экстремальных случаях — возникновение чёрных дыр;
- запаздывание потенциалов, связанное с конечной скоростью распространения гравитационных возмущений;
- как следствие, появление гравитационных волн;
- эффекты нелинейности: гравитационные поля имеют свойство «вмешиваться» в интенсивность друг друга, поэтому принцип суперпозиции в сильных полях уже не выполняется.
Гравитационное излучение
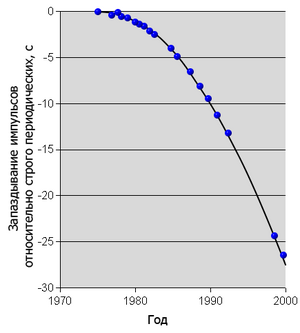
Одним из важных предсказаний ОТО является гравитационное излучение, наличие которого было подтверждено прямыми наблюдениями в 2015 году[9]. Однако и раньше были весомые косвенные свидетельства в пользу его существования, а именно: потери энергии в тесных двойных системах, содержащих компактные гравитирующие объекты (такие как нейтронные звезды или чёрные дыры), в частности, обнаруженные в 1979 году в знаменитой системе PSR B1913+16 (пульсаре Халса — Тейлора) — хорошо согласуются с моделью ОТО, в которой эта энергия уносится именно гравитационным излучением[10].
Гравитационное излучение могут генерировать только системы с переменным квадрупольным или более высокими мультипольными моментами, этот факт говорит о том, что гравитационное излучение большинства природных источников направленное, что существенно усложняет его обнаружение. Мощность гравитационного [math]\displaystyle{ n }[/math] -польного источника пропорциональна [math]\displaystyle{ (v/c)^{2n + 2} }[/math], если мультиполь имеет электрический тип, и [math]\displaystyle{ (v/c)^{2n + 4} }[/math] — если мультиполь магнитного типа[11], где [math]\displaystyle{ v }[/math] — характерная скорость движения источников в излучающей системе, а [math]\displaystyle{ c }[/math] — скорость света в вакууме. Таким образом, доминирующим моментом будет квадрупольный момент электрического типа, а мощность соответствующего излучения равна:
- [math]\displaystyle{ L = \frac{1}{5}\frac{G}{c^5}\left\langle \frac{d^3 Q_{ij}}{dt^3} \frac{d^3 Q^{ij}}{dt^3}\right\rangle, }[/math]
где [math]\displaystyle{ Q_{ij} }[/math] — тензор квадрупольного момента распределения масс излучающей системы. Константа [math]\displaystyle{ \frac{G}{c^5} = 2{,}76 \cdot 10^{-53} }[/math] (1/Вт) позволяет оценить порядок величины мощности излучения.
Начиная с 1969 года (эксперименты Вебера[англ.]), создаются детекторы гравитационного излучения. В США, Европе и Японии в настоящий момент существует несколько действующих наземных детекторов (LIGO, VIRGO, TAMA[англ.], GEO 600), а также проект космического гравитационного детектора LISA (Laser Interferometer Space Antenna — лазерно-интерферометрическая космическая антенна). Наземный детектор в России разрабатывается в Научном центре гравитационно-волновых исследований «Дулкын»[12] республики Татарстан.
Тонкие эффекты гравитации

Помимо классических эффектов гравитационного притяжения и замедления времени, общая теория относительности предсказывает существование других проявлений гравитации, которые в земных условиях весьма слабы и поэтому их обнаружение и экспериментальная проверка весьма затруднительны. До последнего времени преодоление этих трудностей представлялось за пределами возможностей экспериментаторов.
Среди них, в частности, можно назвать увлечение инерциальных систем отсчёта (или эффект Лензе — Тирринга) и гравитомагнитное поле. В 2005 году автоматический аппарат НАСА Gravity Probe B провёл беспрецедентный по точности эксперимент по измерению этих эффектов вблизи Земли. Обработка полученных данных велась до мая 2011 года и подтвердила существование и величину эффектов геодезической прецессии и увлечения инерциальных систем отсчёта, хотя и с точностью, несколько меньшей изначально предполагавшейся.
После интенсивной работы по анализу и извлечению помех измерений, окончательные итоги миссии были объявлены на пресс-конференции по NASA-TV 4 мая 2011 года и опубликованы в Physical Review Letters[13]. Измеренная величина геодезической прецессии составила −6601,8±18,3 миллисекунды дуги в год, а эффекта увлечения — −37,2±7,2 миллисекунды дуги в год (ср. с теоретическими значениями −6606,1 mas/год и −39,2 mas/год).
Классические теории гравитации
В связи с тем, что квантовые эффекты гравитации чрезвычайно малы даже в самых экстремальных и наблюдательных условиях, до сих пор не существует их надёжных наблюдений. Теоретические оценки показывают, что в подавляющем большинстве случаев можно ограничиться классическим описанием гравитационного взаимодействия.
Существует современная каноническая[14] классическая теория гравитации — общая теория относительности, и множество уточняющих её гипотез и теорий различной степени разработанности, конкурирующих между собой. Все эти теории дают очень похожие предсказания в рамках того приближения, в котором в настоящее время осуществляются экспериментальные тесты. Далее описаны несколько основных, наиболее хорошо разработанных или известных теорий гравитации.
Общая теория относительности
В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причём пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии. Гравитационное поле (обобщение ньютоновского гравитационного потенциала), иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем — метрикой четырёхмерного пространства-времени, а напряжённость гравитационного поля — с аффинной связностью пространства-времени, определяемой метрикой.
Стандартной задачей ОТО является определение компонент метрического тензора, в совокупности задающих геометрические свойства пространства-времени, по известному распределению источников энергии-импульса в рассматриваемой системе четырёхмерных координат. В свою очередь знание метрики позволяет рассчитывать движение пробных частиц, что эквивалентно знанию свойств поля тяготения в данной системе. В связи с тензорным характером уравнений ОТО, а также со стандартным фундаментальным обоснованием её формулировки, считается, что гравитация также носит тензорный характер. Одним из следствий является то, что гравитационное излучение должно быть не ниже квадрупольного порядка.
Известно, что в ОТО имеются затруднения в связи с неинвариантностью энергии гравитационного поля, поскольку данная энергия не описывается тензором и может быть теоретически определена разными способами. В классической ОТО также возникает проблема описания спин-орбитального взаимодействия (так как спин протяжённого объекта также не имеет однозначного определения). Считается, что существуют определённые проблемы с однозначностью результатов и обоснованием непротиворечивости (проблема гравитационных сингулярностей).
Однако экспериментально ОТО подтверждается до самого последнего времени (2012 год). Кроме того, многие альтернативные эйнштейновскому, но стандартные для современной физики подходы к формулировке теории гравитации приводят к результату, совпадающему с ОТО в низкоэнергетическом приближении, которое только и доступно сейчас экспериментальной проверке.
Теория Эйнштейна — Картана
Теория Эйнштейна — Картана (ЭК) была разработана как расширение ОТО, внутренне включающее в себя описание воздействия на пространство-время, кроме энергии-импульса, также и спина объектов[15]. В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана — Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса: один из них аналогичен ОТО, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением; второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения.
Получаемые поправки к ОТО, в условиях современной Вселенной, настолько малы, что пока не видно даже гипотетических путей для их измерения.
Теория Бранса — Дикке
В скалярно-тензорных теориях, самой известной из которых является теория Бранса — Дикке (или Йордана — Бранса — Дикке), гравитационное поле как эффективная метрика пространства-времени определяется воздействием не только тензора энергии-импульса материи, как в ОТО, но и дополнительного гравитационного скалярного поля. Источником скалярного поля считается свёрнутый тензор энергии-импульса материи. Следовательно, скалярно-тензорные теории, как ОТО и РТГ (Релятивистская теория гравитации), относятся к метрическим теориям, дающим объяснение гравитации, используя только геометрию пространства-времени и его метрические свойства. Наличие скалярного поля приводит к двум группам уравнений для компонент гравитационного поля: одна для метрики, вторая — для скалярного поля. Теория Бранса — Дикке вследствие наличия скалярного поля может рассматриваться также как действующая в пятимерном многообразии, состоящем из пространства-времени и скалярного поля[16].
Подобное распадение уравнений на два класса имеет место и в РТГ, где второе тензорное уравнение вводится для учёта связи между неевклидовым пространством и пространством Минковского[17]. Благодаря наличию безразмерного параметра в теории Йордана — Бранса — Дикке появляется возможность выбрать его так, чтобы результаты теории совпадали с результатами гравитационных экспериментов. При этом при стремлении параметра к бесконечности предсказания теории становятся всё более близкими к ОТО, так что опровергнуть теорию Йордана — Бранса — Дикке невозможно никаким экспериментом, подтверждающим общую теорию относительности.
Квантовая теория гравитации
Несмотря на более чем полувековую историю попыток, гравитация — единственное из фундаментальных взаимодействий, для которого пока ещё не построена общепризнанная непротиворечивая квантовая теория. При низких энергиях, в духе квантовой теории поля, гравитационное взаимодействие можно представить как обмен гравитонами — калибровочными бозонами со спином 2. Однако получающаяся теория неперенормируема, и поэтому считается неудовлетворительной.
В последние десятилетия разработаны несколько перспективных подходов к решению задачи квантования гравитации: теория струн, петлевая квантовая гравитация и прочие.
- Теория струн
В ней вместо частиц и фонового пространства-времени выступают струны и их многомерные аналоги — браны. Для многомерных задач браны являются многомерными частицами, но с точки зрения частиц, движущихся внутри этих бран, они являются пространственно-временными структурами. Вариантом теории струн является М-теория.
- Петлевая квантовая гравитация
В ней делается попытка сформулировать квантовую теорию поля без привязки к пространственно-временному фону, пространство и время по этой теории состоят из дискретных частей. Эти маленькие квантовые ячейки пространства определённым способом соединены друг с другом, так что на малых масштабах времени и длины они создают пёструю, дискретную структуру пространства, а на больших масштабах плавно переходят в непрерывное гладкое пространство-время. Хотя многие космологические модели могут описать поведение вселенной только от Планковского времени после Большого Взрыва, петлевая квантовая гравитация может описать сам процесс взрыва, и даже заглянуть раньше. Петлевая квантовая гравитация позволяет описать все частицы стандартной модели, не требуя для объяснения их масс введения бозона Хиггса.
- Причинная динамическая триангуляция
Причинная динамическая триангуляция — пространственно-временное многообразие в ней строится из элементарных евклидовых симплексов (треугольник, тетраэдр, пентахор) размеров порядка планковских с учётом принципа причинности. Четырёхмерность и псевдоевклидовость пространства-времени в макроскопических масштабах в ней не постулируются, а являются следствием теории.
Гравитация в микромире
Гравитация в микромире при низких энергиях элементарных частиц на много порядков слабее остальных фундаментальных взаимодействий. Так, отношение силы гравитационного взаимодействия двух покоящихся протонов к силе электростатического взаимодействия равно [math]\displaystyle{ 10^{-36} }[/math].
Для сравнения закона всемирного тяготения с законом Кулона величину [math]\displaystyle{ \sqrt{G_{N}}m }[/math] называют гравитационным зарядом. В силу принципа эквивалентности массы и энергии гравитационный заряд равен [math]\displaystyle{ \sqrt{G_{N}}\frac{E}{c^{2}} }[/math]. Гравитационное взаимодействие становится равным по силе электромагнитному, когда гравитационный заряд равен электрическому [math]\displaystyle{ \sqrt{G_{N}}\frac{E}{c^{2}} = e }[/math], то есть при энергиях [math]\displaystyle{ E = \frac{ec^{2}}{\sqrt{G_{N}}} = 10^{18} }[/math] ГэВ, пока недостижимых на ускорителях элементарных частиц.[18][19]
Предполагается, что гравитационное взаимодействие было таким же сильным, как и остальные взаимодействия в первые [math]\displaystyle{ 10^{-43} }[/math] секунд после Большого взрыва[20].
Примечания
- ↑ Вайнберг С. Первые три минуты. — М.: Энергоиздат, 1981. — С. 135.
- ↑ Нарликар Дж. Неистовая вселенная. — М.: Мир, 1985. — С. 25. — Тираж 100 000 экз.
- ↑ Нарликар Дж. Гравитация без формул. — М.: Мир, 1985. — С. 144. — Тираж 50 000 экз.
- ↑ Сивухин Д. В. Общий курс физики. Механика. — М., Наука, 1979. — Тираж 50 000 экз. — с. 311.
- ↑ В. Паули Нарушение зеркальной симметрии в законах атомной физики // Теоретическая физика 20 века. Памяти Вольфганга Паули. — М., ИЛ, 1962. — c. 383
- ↑ Improved Determination of G Using Two Methods // Phys. Rev. Lett. 111, 101102 (2013), DOI:10.1103/PhysRevLett.111.101102
- ↑ G. Rosi, F. Sorrentino, L. Cacciapuoti, M. Prevedelli, G. M. Tino. Precision measurement of the Newtonian gravitational constant using cold atoms. Nature (18 июня 2014).
- ↑ Нарликар Дж. Неистовая вселенная. — М.: Мир, 1985. — С. 70. — Тираж 100 000 экз.
- ↑ LIGO Scientific Collaboration and Virgo Collaboration, B. P. Abbott, R. Abbott, T. D. Abbott, M. R. Abernathy. Observation of Gravitational Waves from a Binary Black Hole Merger // Physical Review Letters. — 2016-02-11. — Т. 116, вып. 6. — С. 061102. — doi:10.1103/PhysRevLett.116.061102.
- ↑ Нарликар Дж. Гравитация без формул. — М.: Мир, 1985. — С. 87. — Тираж 50 000 экз.
- ↑ См. аналогию между слабым гравитационным полем и электромагнитным полем в статье гравитомагнетизм.
- ↑ Научный Центр Гравитационно-Волновых Исследований «Дулкын» Архивная копия от 25 сентября 2006 на Wayback Machine
- ↑ C. W. F. Everitt et al. Gravity Probe B: Final results of a space experiment to test general relativity, Physical Review Letters (1 мая 2011). Дата обращения 6 мая 2011.
- ↑ Канонической эта теория является в том смысле, что она наиболее хорошо разработана и широко используется в современной небесной механике, астрофизике и космологии, причём количество надёжно установленных противоречащих ей экспериментальных результатов практически равно нулю.
- ↑ Иваненко Д. Д., Пронин П. И., Сарданашвили Г. А. Калибровочная теория гравитации. — М.: Изд. МГУ, 1985.
- ↑ Brans, C. H.; Dicke, R. H. (November 1 1961). «Mach’s Principle and a Relativistic Theory of Gravitation». Physical Review 124 (3): 925—935. DOI:10.1103/PhysRev.124.925. Retrieved on 2006-09-23.
- ↑ С ортодоксальной точки зрения это уравнение представляет собой координатное условие.
- ↑ Яворский Б. М., Детлаф А. А., Лебедев А. К. Справочник по физике для инженеров и студентов вузов. — М.: Оникс, 2007. — С. 948. — ISBN 978-5-488-01248-6 — Тираж 5100 экз.
- ↑ Нарликар Дж. Гравитация без формул. — М.: Мир, 1985. — С. 145. — Тираж 50 000 экз.
- ↑ Вайнберг С. Первые три минуты. — М.: Энергоиздат, 1981. — С. 136.
Литература
- Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900—1915). — М.: Наука, 1981. — 352c.
- Визгин В. П. Единые теории в 1-й трети XX в. — М.: Наука, 1985. — 304c.
- Иваненко Д. Д., Сарданашвили Г. А. Гравитация. 3-е изд. — М.: УРСС, 2008. — 200с.
- Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977.
- Торн К. Чёрные дыры и складки времени. Дерзкое наследие Эйнштейна. — М.: Государственное издательство физико-математической литературы, 2009.
- Halliday, David; Robert Resnick; Kenneth S. Krane. Physics v. 1. — New York: John Wiley & Sons, 2001. — ISBN 978-0-471-32057-9.
- Serway, Raymond A.; Jewett, John W. Physics for Scientists and Engineers. — 6th. — Brooks/Cole[англ.], 2004. — ISBN 978-0-534-40842-8.
- Tipler, Paul. Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (англ.). — 5th. — W.H. Freeman[англ.], 2004. — ISBN 978-0-7167-0809-4.
Ссылки
- Физическая энциклопедия — «Тяготение»
- Hazewinkel, Michiel, ed. (2001), Gravitation, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Hazewinkel, Michiel, ed. (2001), Gravitation, theory of, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4