Корни из единицы

Корни пятой степени из единицы (вершины пятиугольника)

Корни n-й степени из единицы — комплексные корни многочлена [math]\displaystyle{ x^n-1 }[/math], где [math]\displaystyle{ n \geqslant 1 }[/math]. Другими словами, это комплексные числа, n-я степень которых равна 1. В общей алгебре рассматриваются также корни многочлена [math]\displaystyle{ x^n - 1 }[/math] не только в комплексном, но и в произвольном ином поле, характеристика [math]\displaystyle{ p }[/math] которого не является делителем степени [math]\displaystyle{ n }[/math] многочлена.

Корни из единицы широко используются в математике, особенно в теории чисел, быстром преобразовании Фурье, теории расширений полей, теории построений циркулем и линейкой, представлениях групп.

Представление

Представим комплексную единицу в тригонометрическом виде:

[math]\displaystyle{ 1 = \cos 0 + i \sin 0. }[/math]

Тогда по формуле Муавра получим выражение для [math]\displaystyle{ k }[/math]-го корня n-й степени из единицы [math]\displaystyle{ u_k }[/math]:

[math]\displaystyle{ u_k = \cos\frac{2\pi k}{n} + i \sin\frac{2\pi k}{n}, \quad k = 0, 1, \dots, n - 1. }[/math]

Корни из единицы могут также быть представлены в показательной форме:

[math]\displaystyle{ u_k = e^{\frac{2\pi k}{n} i}, \quad k = 0, 1, \dots, n - 1. }[/math]

Из этих формул вытекает, что корней n-й степени из единицы всегда ровно [math]\displaystyle{ n }[/math], и все они различны.

Примеры

Кубические корни из единицы

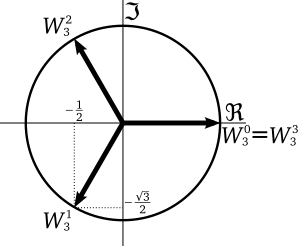
Кубические корни из единицы:

[math]\displaystyle{ \left\{1, \frac{-1 + i \sqrt{3}}{2}, \frac{-1 - i \sqrt{3}}{2} \right\}. }[/math]

Корни 4-й степени из единицы:

[math]\displaystyle{ \left\{1, +i, -1, -i \right\}. }[/math]

Для корня 5-й степени имеются 4 порождающих элемента, степени каждого из которых охватывают все корни 5-й степени:

[math]\displaystyle{ \Big\{e^{\frac{2 \pi i k}{5}} \,\Big|\, k \in \{1, 2, 3, 4\}\Big\} = \left\{\left. \frac{u \sqrt{5} - 1}{4} + v\sqrt{\frac{5 + u\sqrt{5}}8}i \,\right|\, u, v \in \{-1, 1\}\right\}. }[/math]

Для корня 6-й степени порождающих элементов только два ([math]\displaystyle{ u_1 }[/math] и [math]\displaystyle{ u_5 }[/math]):

[math]\displaystyle{ \left\{ \frac{1 + i \sqrt{3}}{2}, \frac{1 - i \sqrt{3}}{2} \right\}. }[/math]

Свойства

Геометрические свойства

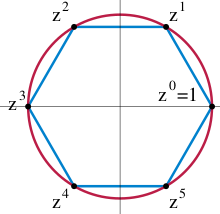
Модуль каждого корня равен 1. На комплексной плоскости корни из единицы образуют вершины правильного многоугольника, вписанного в единичную окружность. Одной из вершин всегда является комплексная единица [math]\displaystyle{ 1 + 0i. }[/math] Вещественных корней может быть либо два, если [math]\displaystyle{ n }[/math] чётно (единица и минус единица), либо один (единица), если [math]\displaystyle{ n }[/math] нечётно. В любом случае невещественных корней чётное число, они располагаются симметрично относительно горизонтальной оси. Последнее означает, что если [math]\displaystyle{ u_k }[/math] — корень из единицы, то сопряжённое к нему число [math]\displaystyle{ \overline{u_k} }[/math] — тоже корень из единицы.

Пусть M — произвольная точка единичной окружности и [math]\displaystyle{ n \gt 1. }[/math] Тогда сумма квадратов расстояний от M до всех корней [math]\displaystyle{ n }[/math]-й степени из единицы равна [math]\displaystyle{ 2n }[/math].

Алгебраические свойства

Корни из единицы представляют собой целые алгебраические числа.

Корни из единицы образуют по умножению коммутативную конечную группу порядка [math]\displaystyle{ n }[/math]. В частности, любая целая степень корня из единицы тоже является корнем из единицы. Обратный элемент для каждого элемента этой группы совпадает с сопряжённым ему. Нейтральным элементом группы является комплексная единица.

Корни 6-й степени из единицы как степени первого порождающего элемента

Группа корней из единицы изоморфна аддитивной группе классов вычетов [math]\displaystyle{ \mathbb{Z}_n. }[/math] Отсюда следует, что она является циклической группой; в качестве порождающего (первообразного) можно взять любой элемент [math]\displaystyle{ u_k }[/math], индекс [math]\displaystyle{ k }[/math] которого взаимно прост с [math]\displaystyle{ n }[/math].

• Следствия:
  • элемент [math]\displaystyle{ u_1 }[/math] всегда является первообразным (его часто называют главным корнем из единицы);
  • если [math]\displaystyle{ n }[/math] — простое число, то степени любого корня, кроме [math]\displaystyle{ \pm 1 }[/math], охватывают всю группу (то есть все корни, кроме [math]\displaystyle{ \pm 1 }[/math], являются первообразными);
  • число первообразных корней равно [math]\displaystyle{ \varphi(n) }[/math], где [math]\displaystyle{ \varphi }[/math] — функция Эйлера.

Если [math]\displaystyle{ n \gt 1 }[/math], то для любого первообразного корня из единицы [math]\displaystyle{ u }[/math] имеют место формулы

[math]\displaystyle{ \sum_{k=0}^{n-1} u^k = \frac{u^n - 1}{u - 1} = 0, }[/math]

[math]\displaystyle{ \prod_{k=1}^{n-1} |1 - u_k| = n. }[/math]

Круговые поля

Основная статья: Круговое поле

Круговое поле, или поле деления круга степени n — это поле [math]\displaystyle{ K_n = \mathbb{Q}(u) }[/math], порождённое присоединением к полю рациональных чисел [math]\displaystyle{ \mathbb{Q} }[/math] первообразного корня n-й степени из единицы [math]\displaystyle{ u }[/math]. Круговое поле является подполем поля комплексных чисел; оно содержит все корни n-й степени из единицы, а также результаты арифметических действий над ними.

Исследование круговых полей сыграло значительную роль в создании и развитии теории целых алгебраических чисел, теории чисел и теории Галуа.

Пример: [math]\displaystyle{ K_3 }[/math] состоит из комплексных чисел вида [math]\displaystyle{ a + b \sqrt{3}\,i }[/math], где [math]\displaystyle{ a, b }[/math] — рациональные числа.

Теорема Кронекера — Вебера: всякое абелево конечное расширение поля рациональных чисел содержится в некотором круговом поле.

Обобщения

Корни из единицы n-й степени можно определить не только для комплексных чисел, но и для любого другого алгебраического поля [math]\displaystyle{ K }[/math] как решения уравнения [math]\displaystyle{ x^n=1 }[/math], где [math]\displaystyle{ 1 }[/math] — единица поля [math]\displaystyle{ K }[/math]. Корни из единицы существуют в любом поле и образуют подгруппу мультипликативной группы поля [math]\displaystyle{ K }[/math]. Обратно, любая конечная подгруппа мультипликативной группы поля [math]\displaystyle{ K }[/math] содержит только корни из единицы и является циклической.

Если характеристика поля ненулевая, то группа корней из единицы совместно с нулём образует конечное поле.

История

Широкое применение корней из единицы как инструмента исследования начал Гаусс. В своей монографии «Арифметические исследования» (1801) он впервые решил древнюю задачу о делении окружности циркулем и линейкой на n равных частей (или, что то же, о построении правильного многоугольника с n сторонами). С помощью корней из единицы Гаусс свёл задачу к решению уравнения деления круга:

[math]\displaystyle{ x^{n-1} + x^{n-2} + \ldots + x + 1 = 0. }[/math]

Дальнейшие рассуждения Гаусса показали, что задача имеет решение, только если n может быть представлено в виде [math]\displaystyle{ 2^{2^r} + 1 }[/math]. Подход Гаусса использовали позднее Лагранж и Якоби. Коши применил корни из единицы для исследования более общей задачи решения алгебраических уравнений со многими неизвестными (1847 год).

Новые применения корней из единицы обнаружились после создания в начале XX века абстрактной алгебры. Эмми Нётер и Эмиль Артин использовали это понятие в теории расширений полей и обобщении теории Галуа.

См. также

• Круговой многочлен
• Первообразный корень из единицы

Литература

• Бурбаки Н. Алгебра. Многочлены и поля. Упорядоченные группы. — М.: Наука, 1965. — С. 188 и далее. — 299 с.
• Ван дер Варден Б. Л. Алгебра. Определения, теоремы, формулы. — СПб.: Лань, 2004. — 624 с. — ISBN 5-8114-0552-9. Архивная копия от 4 марта 2016 на Wayback Machine
• Корень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 15.
• Milne, James S. Algebraic Number Theory (неопр.). Course Notes (1998). Архивировано 2 апреля 2012 года.

Ссылки

• Комплексные корни n-й степени из единицы и решение уравнений.