Экспонента
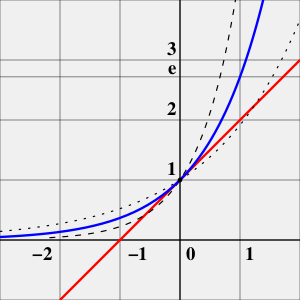
Касательная (красным) в нуле у функции [math]\displaystyle{ e^x }[/math] наклонена на [math]\displaystyle{ \frac {\pi}{4} ~ (45^{\circ}) }[/math].
Рядом для примера показаны [math]\displaystyle{ y=2^x }[/math] (точками) и [math]\displaystyle{ y=4^x }[/math] (штрихами)
Экспоне́нта — показательная функция [math]\displaystyle{ f(x)=\exp(x)=e^x }[/math], где [math]\displaystyle{ e \approx 2{,}718 }[/math] — число Эйлера.
Определение
Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:
- [math]\displaystyle{ e^x = 1 + \sum_{n = 1}^{\infty} {x^n \over n!} = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots }[/math]
или через предел:
- [math]\displaystyle{ e^x=\lim_{n\rightarrow \infty} \left( 1+\frac{x}{n} \right)^n }[/math].
Здесь [math]\displaystyle{ x }[/math] — любое комплексное число.
Происхождение понятия
Слово экспонента происходит от лат. "exponere", что переводится как "выставить вперёд; показать", которое в свою очередь произошло от лат. приставки "ex-" ("впереди") и лат. слова "ponere" ("ставить, расположить");[1] Смысл использования такого слова для показателя степени заключается в том, что знак экспоненты "ставят вне" привычной линии письма [math]\displaystyle{ a^x }[/math](немного выше и правее места, где обычно должна быть поставлена цифра).
Свойства
- [math]\displaystyle{ (e^x)'=e^x }[/math], а в частности, экспонента — единственное решение дифференциального уравнения [math]\displaystyle{ y'=y }[/math] с начальными данными [math]\displaystyle{ y(0)=1 }[/math]. Кроме того, через экспоненту выражаются общие решения однородных дифференциальных уравнений.
- Экспонента определена на всей вещественной оси. На ней экспонента всюду возрастает и строго больше нуля.
- Экспонента — выпуклая функция.
- Обратная функция к ней — натуральный логарифм [math]\displaystyle{ (\ln x) }[/math].
- Преобразование Фурье экспоненты — обобщённая функция, а именно дельта-функция Дирака.
- Преобразование Лапласа экспоненты [math]\displaystyle{ e^{ax} }[/math] определено в области [math]\displaystyle{ \operatorname{Re}(x) \lt a }[/math].
- Производная в нуле равна [math]\displaystyle{ 1 }[/math], поэтому касательная к экспоненте в этой точке проходит под углом [math]\displaystyle{ 45^{\circ} }[/math] или [math]\displaystyle{ \frac{\pi}{4} }[/math].
- Основное функциональное свойство экспоненты, как и всякой показательной функции:
- [math]\displaystyle{ \exp(a+b)=\exp(a)\exp(b) }[/math].
- Непрерывная функция с таким свойством либо тождественно равна [math]\displaystyle{ 0 }[/math], либо имеет вид [math]\displaystyle{ \exp(cx) }[/math], где [math]\displaystyle{ c }[/math] — некоторая константа.
- [math]\displaystyle{ e^x = \operatorname{sh} x + \operatorname{ch} x }[/math], где [math]\displaystyle{ \operatorname{sh} }[/math] и [math]\displaystyle{ \operatorname{ch} }[/math] — гиперболические синус и косинус.
Комплексная экспонента

Легенда
Комплексная экспонента — математическая функция, задаваемая соотношением [math]\displaystyle{ f(z)=e^z }[/math], где [math]\displaystyle{ z }[/math] есть комплексное число. Комплексная экспонента определяется как аналитическое продолжение экспоненты [math]\displaystyle{ f(x)=e^x }[/math] вещественного переменного [math]\displaystyle{ x }[/math]:
Определим формальное выражение
- [math]\displaystyle{ e^z=e^{x+iy}=e^x\cdot e^{iy} }[/math].
Определённое таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции [math]\displaystyle{ e^z }[/math], то есть показать, что [math]\displaystyle{ e^z }[/math] разлагается в некоторый сходящийся к данной функции ряд. Покажем это:
- [math]\displaystyle{ f(z)=e^z=e^x\cdot e^{iy}=e^{iy}\sum_{n=0}^\infty\frac{x^n}{n!} }[/math].
Сходимость данного ряда легко доказывается:
- [math]\displaystyle{ \left|e^{iy}\sum_{n=0}^\infty\frac{x^n}{n!}\right|\le\left|\sum_{n=0}^\infty\frac{x^n}{n!}\right|\le\sum_{n=0}^\infty\left|\frac{x^n}{n!}\right|= \sum_{n=0}^{\infty}\dfrac{|x|^n}{n!} =e^{|x|} }[/math].
Ряд всюду сходится абсолютно, то есть вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции [math]\displaystyle{ f(z)=e^z }[/math]. Согласно теореме единственности, полученное продолжение будет единственно, следовательно, на комплексной плоскости функция [math]\displaystyle{ e^z }[/math] всюду определена и аналитична.
Свойства
- Комплексная экспонента — целая голоморфная функция на всей комплексной плоскости. Ни в одной точке она не обращается в ноль.
- [math]\displaystyle{ e^z }[/math] — периодическая функция с основным периодом 2πi: [math]\displaystyle{ e^{i\varphi}=e^{i(\varphi+2\pi)} }[/math]. В силу периодичности комплексная экспонента бесконечнолистна. В качестве её области однолистности можно выбрать любую горизонтальную полосу высотой [math]\displaystyle{ 2 \pi }[/math].
- [math]\displaystyle{ e^z }[/math] — единственная с точностью до постоянного множителя функция, производная (а соответственно, и первообразная) которой совпадает с исходной функцией.
- Алгебраически экспонента от комплексного аргумента [math]\displaystyle{ z=x+iy }[/math] может быть определена следующим образом:
- [math]\displaystyle{ e^z=e^{x+iy}=e^xe^{iy}=e^x(\cos \, y + i\sin \, y) }[/math] (формула Эйлера).
- В частности, имеет место тождество Эйлера:
- [math]\displaystyle{ e^{i\pi}+1=0. }[/math]
Вариации и обобщения
Аналогично экспонента определяется для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.
Матричная экспонента
Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:
- [math]\displaystyle{ \exp A=\sum_{k=0}^{\infty} \frac{A^k}{k!}. }[/math]
Определённый таким образом ряд сходится для любого оператора [math]\displaystyle{ A }[/math] с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы [math]\displaystyle{ A\colon }[/math] [math]\displaystyle{ \exp \|A\|. }[/math] Следовательно, экспонента от матрицы [math]\displaystyle{ A \in \mathbb{R}^{n\times n} }[/math] всегда определена и сама является матрицей.
С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение [math]\displaystyle{ \dot x=Ax, ~~~ x\in \mathbb R^n }[/math] с начальным условием [math]\displaystyle{ x(0)=x_0 }[/math] имеет своим решением [math]\displaystyle{ x(t)=\exp (At) x_0. }[/math]
h-экспонента
Введение [math]\displaystyle{ h }[/math]-экспоненты основано на втором замечательном пределе:
- [math]\displaystyle{ e_{h}(x)=(1+h)^\frac{x}{h}. }[/math]
При [math]\displaystyle{ h\to 0 }[/math] получается обычная экспонента[2].
Обратная функция
Обратная функция к экспоненциальной функции — натуральный логарифм. Обозначается [math]\displaystyle{ \ln x }[/math]:
- [math]\displaystyle{ \ln x = \log_{e} x. }[/math]
См. также
Примечания
Литература
- Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — Издание 5-е, исправленное. — М.: Наука, 1987. — 688 с.
- Хапланов М. Г. Теория функции комплексного переменного (краткий курс). — Издание 2-е, исправленное. — М.: Просвещение, 1965. — 209 с.