Частица в периодическом потенциале

В квантовой механике задача о частице в одномерном периодическом потенциале — идеализированная задача, которая может быть решена точно (при некоторых специального вида потенциалах), без упрощений. Предполагается, что потенциал задан на всем бесконечном пространстве и периодичен, то есть обладает трансляционной симметрией, что, вообще говоря, не выполняется для реальных кристаллов, где всегда существует как минимум один дефект — поверхность (это приводит к другой задаче о поверхностных состояниях или таммовских уровнях).

Общий вид спектра

Периодическая задача

Рассмотрим одномерную решётку ионов, расстояние между которыми [math]\displaystyle{ a }[/math]. Потенциал при этом будет периодическим. Рассмотрим сначала идеализированный случай бесконечного кристалла. Уравнение Шрёдингера имеет вид:

[math]\displaystyle{ -\frac{\hbar^2}{2m}\frac{\partial^2 \psi (x)}{\partial x^2} + V_a(x) \psi (x) = E \psi (x) }[/math]

с периодическим потенциалом [math]\displaystyle{ V_a(x) = V_a(x+a). }[/math] Спектр определяется как множество тех энергий, при которых уравнение имеет решения, ограниченные (не стремящиеся к нулю или бесконечности) на всей вещественной оси. Уравнение Шрёдингера имеет второй порядок, соответственно пространство решений является двумерным. Пусть [math]\displaystyle{ \psi_{1,2} }[/math] — линейно независимые решения уравнения. Тогда при сдвиге на период, в силу периодичности задачи, они преобразуются через друг друга:

[math]\displaystyle{ \left( \begin{matrix} \psi_1(x+a) \\ \psi_2(x+a) \end{matrix} \right) = \mathrm{T} \left( \begin{matrix} \psi_1(x) \\ \psi_2(x) \end{matrix} \right) }[/math]

где [math]\displaystyle{ \mathrm{T} }[/math] — некоторая матрица (матрица монодромии). Рассматривая вронскиан, несложно показать, что [math]\displaystyle{ \mathrm{T} }[/math] унитарна и [math]\displaystyle{ \det \mathrm{T} = 1 }[/math]. Отсюда следует, что в некотором базисе она имеет вид

[math]\displaystyle{ \mathrm{T} = \left( \begin{matrix} e^{\mathrm{i}ka} & 0 \\ 0 & e^{-\mathrm{i}ka} \end{matrix} \right) }[/math]

Отсюда следует теорема Блоха: соответствующие собственные функции имеют вид

[math]\displaystyle{ \psi_{1,2} (x) = e^{\mathrm{i}kx} \phi_{1,2}(x), }[/math]

где [math]\displaystyle{ \phi_{1,2}(x) }[/math] — периодические функции. Заметим, что пока что [math]\displaystyle{ k\in\Complex }[/math]. Очевидно, что спектру соответствуют [math]\displaystyle{ k\in\R }[/math], что равносильно (с учётом унитарности) условию на след матрицы монодромии

[math]\displaystyle{ \mathrm{Tr}\ \mathrm{T} = 2\cos(kx) \in [-2; 2] }[/math]

Несложно показать, что [math]\displaystyle{ \mathrm{Tr}( \mathrm{T})(E) }[/math] есть гладкая функция. Отсюда следует зонная структура спектра: для частицы в периодическом потенциале допустимые уровни энергии — это некоторое, обычно бесконечное, множество отрезков на вещественной оси. Для потенциала общего вида спектр не имеет изолированных точек, при малом шевелении потенциала они либо исчезают, либо превращаются в зоны малой ширины. Заметим, что крайние отрезки спектра в принципе могут быть неограничены, при этом все уровни энергии, начиная с некоторого, являются допустимыми, а полное число зон конечно (см. конечнозонное интегрирование). В подобной постановке задача допускает полное и простое решение в тэта-функциях.

k называют квазиимпульсом, по аналогии с волновой функцией [math]\displaystyle{ e^{\mathrm{i}kx} }[/math] для частицы с определённым импульсом k. Как видно, вся волновая функция определяется величиной k и любым участком функции длиной a.

Аналогично возникают энергетические зоны в решётках более высоких размерностей.

Влияние границ

В реальном кристалле число допустимых состояний очень велико. Приводящее к этому дополнительное ограничение на величину квазиимпульса возникает из граничных условий на волновую функцию на поверхности кристалла. При этом вместо непрерывных зон возникают области с плотно расположенными дискретными уровнями энергии (разрешённые зоны) и области, в которых состояний вообще нет (запрещённые зоны). Оценим расстояние между уровнями энергии в разрешённых зонах.

Вместо рассмотрения допустимых уровней энергии (для этого потребовалась бы дополнительная информация, вроде дисперсионного соотношения и точной структуры кристалла) рассмотрим допустимые значения квазиимпульса. При рассмотрении изолированного кристалла обычно рассматриваются периодические граничные условия на волновую функцию. Это предположение оправдано, так как точные граничные условия в реальном кристалле состоят в занулении волновой функции электронов на его границе. Для одномерного кристалла это означает чётность волновой функции (0 находится в центре кристалла). Если же влияние границ на волновую функцию мало́, то приближённо можно забыть про точное значение волновой функции на границе, сохранив лишь свойство симметрии — чётность.

Рассмотрим одномерный кристалл длины [math]\displaystyle{ L }[/math]. Граничное условие имеет вид

[math]\displaystyle{ \psi (0)=\psi (L) }[/math]

С учётом теоремы Блоха отсюда следует, что

[math]\displaystyle{ kL = 2\pi n,\; n\in\Z }[/math]

Таким образом, расстояние между соседними допустимыми значениями квазиимпульса равно

[math]\displaystyle{ \Delta k = \frac{2\pi n}{L} }[/math]

Аналогично в общем случае, для кубической решётки:

[math]\displaystyle{ \Delta k_{x,y,z} = \frac{2\pi n}{ L_{x,y,z} } }[/math]

Модель Кронига — Пенни

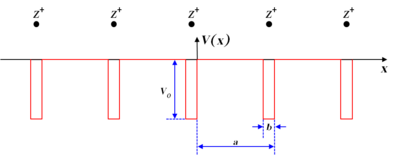
Для упрощения задачи потенциал приближают прямоугольным: используя теорему Блоха. Находят волновую функцию во всём пространстве, но сначала исследуют решение для одного периода, и делают его гладким на краях, то есть «сшивают» значения соседних функций и их производных. Рассмотрим один период потенциала^[1]:
У нас есть две независимых области для которых мы найдём решения:

[math]\displaystyle{ 0\lt x\lt a-b : {-\hbar^2 \over 2m} \psi_{xx} = E \psi\Rightarrow \psi = A e^{i \alpha x} + A' e^{-i \alpha x} \quad \left( \alpha^2 = {2mE \over \hbar^2} \right) }[/math]

[math]\displaystyle{ -b\lt x\lt 0 : {-\hbar^2 \over 2m} \psi_{xx} = (E+V_0)\psi \Rightarrow \psi = B e^{i \beta x} + B' e^{-i \beta x} \quad \left( \beta^2 = {2m(E+V_0) \over \hbar^2} \right) }[/math]

Для нахождения u(x) в каждой области нужно проделать следующие преобразования:

[math]\displaystyle{ \psi(0\lt x\lt a-b) = A e^{i \alpha x} + A' e^{-i \alpha x} = e^{ikx} \cdot \left( A e^{i (\alpha-k) x} + A' e^{-i (\alpha+k) x} \right) }[/math]

[math]\displaystyle{ \Rightarrow u(0\lt x\lt a-b)=A e^{i (\alpha-k) x} + A' e^{-i (\alpha+k) x} }[/math]

Аналогично получим

[math]\displaystyle{ u( -b\lt x\lt 0)=B e^{ i (\beta - k) x} + B' e^{ - i ( \beta + k ) x} \; }[/math]

Чтобы найти полное решение нам надо убедиться в гладкости искомой функции на границах:

[math]\displaystyle{ \psi(0^{-})=\psi(0^{+}) \quad \psi'(0^{-})=\psi'(0^{+}) }[/math]

и периодичности u(x) и u'(x)

[math]\displaystyle{ u(-b)=u(a-b) \quad u'(-b)=u'(a-b). }[/math]

Эти условия дают следующую матрицу:

[math]\displaystyle{ \begin{pmatrix} 1 & 1 & -1 & -1 \\ \alpha & -\alpha & -\beta & \beta \\ e^{i(\alpha-k)(a-b)} & e^{-i(\alpha+k)(a-b)} & -e^{-i(\beta-k)b} & -e^{i(\beta+k)b} \\ (\alpha-k)e^{i(\alpha-k)(a-b)} & -(\alpha+k)e^{-i(\alpha+k)(a-b)} & -(\beta-k)e^{-i(\beta-k)b} & (\beta+k)e^{i(\beta+k)b} \end{pmatrix} \begin{pmatrix} A \\ A' \\ B \\ B' \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} }[/math]

Для существования нетривиального решения необходимо зануление детерминанта этой матрицы. После некоторых преобразований получаем:

[math]\displaystyle{ \cos(k a) = \cos(\beta b) \cos[\alpha(a-b)]-{\alpha^2+\beta^2 \over 2\alpha \beta} \sin(\beta b) \sin[\alpha(a-b)]. \qquad ( * ) }[/math]

Для дальнейшего упрощения мы выполним следующие преобразования, смысл которых заключается в переходе к дельта-образным потенциалам (дираковская гребёнка) :

[math]\displaystyle{ b \rightarrow 0 \ ; \ V_0 \rightarrow \infty \ ; \ V_0 b = \mathrm{constant} }[/math]

[math]\displaystyle{ \Rightarrow \beta b \rightarrow 0 \ ; \ \beta^2 b = \mathrm{constant} \ ; \ \alpha^2 b \rightarrow 0 \ ; \ \sin(\beta b) \rightarrow \beta b \ ; \ \cos(\beta b) \rightarrow 1 }[/math]

Тогда конечный ответ будет:

[math]\displaystyle{ \cos(k a) = \cos(\alpha a)-P{\sin(\alpha a) \over \alpha a} \qquad \left( P={\beta^2 a b \over 2} \right) }[/math]

Программный код

Код для Maple

Следующий программный код написан на языке Maple (9.5). Представляет собой просто графическое решение [math]\displaystyle{ ( * ) }[/math].

  restart;
  with(plots):
  with(stats[statplots]):
  eq:=cos(k*a)=cos(beta*b)*cos(alpha*(a-b)) - (alpha^2+beta^2)/(2*alpha*beta)*sin(beta*b)*sin(alpha*(a-b));
  alpha:=sqrt(8*Pi^2*m*(E)*e/h^2):
  beta:=sqrt(8*Pi^2*m*(E+V)*e/h^2):
  e:=1.6*1e-19:
  a:=0.54310*1e-9:
  m:=0.19*9.1*1e-31:
  b:=1/5*a:
  h:=6.6*1e-34:
  k(E,V):=arccos(rhs(evalf(eq)))/a;

  #График
  p:=plot({subs(V=10,k(E,V)),subs(V=10,-k(E,V))},E=-5..50,labels=[ka, E],color=blue):
  xyexchange(p);

  #Анимация, зависимость от глубины ямы
  p:=animate( plot, [{k(E,V),-k(E,V)},E=-10..50, color=blue,labels=[ka, E]], V=0..30 ):
  xyexchange(p);

На рисунках представлены графические решения уравнения ( * ).

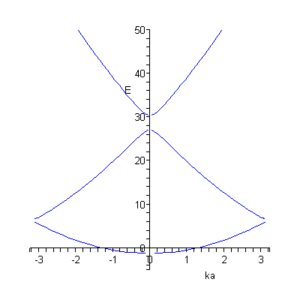Линии отвечают разрешённым значениям энергии. Существуют области по энергии, где ни при каких значениях волнового вектора невозможно существование электрона.

Линии отвечают разрешённым значениям энергии. Показано движение закона дисперсии в зависимости от глубины потенциальной ямы.

На правом рисунке видно, как при некотором значении потенциальной энергии возможно образование одномерного бесщелевого полупроводника.

Код для Scilab

Линии по-прежнему отвечают разрешённым значениям энергии. Синим изображено решение для модели Кронига-Пенни, красным - гребёнки Дирака при тех же значениях V₀b

Код ниже является фактически переводом предшествующей программы на язык Scilab, за тем исключением, что иллюстрирует также и случай перехода к гребёнке Дирака.

clear all

global Pi e a m b h

Pi = 3.1415926;

step = 0.1;

e = 1.6 * 1e-19;
a = 0.54310 * 1e-9;
m = 0.19*9.1 * 1e-31;
b = 1/5 * a;
h = 6.6 * 1e-34;

function [alpha, beta] = ab(V,E)
  alpha = sqrt(8*Pi^2*m*(E)*e/h^2);
  beta  = sqrt(8*Pi^2*m*(E+V)*e/h^2);
endfunction

function r=kronigpenney(V, E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos((cos(beta*b) .* cos(alpha*(a-b)) ) - (alpha.^2+beta.^2) ./ (2*alpha .* beta) .* sin(beta*b) .* sin(alpha*(a-b)));
endfunction

function r=dirac(V,E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos(cos(alpha * a) - (beta.^2 * b * a) ./ 2 .* sin(alpha*a) ./ (alpha * a));
endfunction

E = [1e-3 : step: 50];

k = kronigpenney(10, E);
plot(k, E, 'b'); plot(-k, E, 'b');

k = dirac(10, E);
plot(k, E, 'r'); plot(-k, E, 'r');

Код для Matlab

Код ниже является переводом предшествующей программы на язык Matlab.

function KronigPenneyM

% clear all
% global Pi e a m b h
Pi = 3.1415926;
step = 0.1;

e = 1.6 * 1e-19;
a = 0.54310 * 1e-9;
m = 0.19*9.1 * 1e-31;
b = 1/5 * a;
h = 6.6 * 1e-34;

E = [0 : step: 50];
N = 3;

hold on; 
k = kronigpenney(N, E);
plot([real(k) NaN, -real(k)], [E NaN E], 'b');

k = dirac(N, E);
plot([real(k) NaN, -real(k)], [E NaN E], 'r');

function [alpha, beta] = ab(V,E)
  alpha = sqrt(8*Pi^2*m*(E)*e/h^2);
  beta  = sqrt(8*Pi^2*m*(E+V)*e/h^2);
end

function r=kronigpenney(V, E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos((cos(beta*b) .* cos(alpha*(a-b)) ) - (alpha.^2+beta.^2) / (2*alpha .* beta) .* sin(beta*b) .* sin(alpha*(a-b)));
end

function r=dirac(V,E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos(cos(alpha * a) - (beta.^2 * b * a) / 2 .* sin(alpha*a) / (alpha * a));
end
end

Ссылки

Задачи по квантовой механике. Часть 1. Галицкий, Карнаков, Коган.
1-D periodic potential applet

Примечания

↑ R. de L. Kronig and W. G. Penney. Квантовая механика электронов в кристаллических решётках // Proc. R. Soc. Lond. A. — 1931. — Т. 130. — С. 499—513. — doi:10.1098/rspa.1931.0019.

См. также

[1] R. de L. Kronig and W. G. Penney. Квантовая механика электронов в кристаллических решётках // Proc. R. Soc. Lond. A. — 1931. — Т. 130. — С. 499—513. — doi:10.1098/rspa.1931.0019.

[1]

Модели квантовой механики
Одномерные без учёта спина	Свободная частица Яма с бесконечными стенками Прямоугольная квантовая яма Дельтообразный потенциал Треугольная квантовая яма Гармонический осциллятор Потенциальная ступенька Потенциальная яма Пёшль — Теллера Модифицированная потенциальная яма Пёшль — Теллера Частица в периодическом потенциале Дираковская потенциальная гребёнка Частица в кольце
Многомерные без учёта спина	Круговой осциллятор Ион молекулы водорода Симметричный волчок Сферически-симметрические потенциалы Потенциал Вудса — Саксона Задача Кеплера Потенциал Юкавы Потенциал Морзе Потенциал Хюльтена Молекулярный потенциал Кратцера Экспоненциальный потенциал
С учётом спина	Атом водорода Гидрид-ион Атом гелия

Методы расчета электронной структуры
Теория валентных связей	Гибридизация орбиталей Теория резонанса Двухэлектронная трёхцентровая связь Двойная связь Тройная связь
Теория молекулярных орбиталей	Метод линейных комбинаций атомных орбиталей Метод Хартри — Фока Метод связанных кластеров Квантовый метод Монте-Карло
Зонная теория	Метод kp Метод псевдопотенциала Приближение сильно связанных электронов Приближение почти свободных электронов Метод присоединённых плоских волн Метод функции Грина Теория функционала плотности MT-потенциал