Вычитание

Вычита́ние (убавление) — одна из вспомогательных бинарных математических операций (арифметических действий) двух аргументов (уменьшаемого и вычитаемого), результатом которой является новое число (разность)[1], получаемое уменьшением значения первого аргумента на значение второго аргумента. На письме обычно обозначается с помощью знака «минус»: [math]\displaystyle{ a-b=c }[/math] . Вычитание — операция обратная сложению.
В общем виде можно записать: [math]\displaystyle{ \overline{S}(a, b)=c }[/math], где [math]\displaystyle{ a \in A }[/math] и [math]\displaystyle{ b \in A }[/math]. То есть каждой паре элементов [math]\displaystyle{ (a,b) }[/math] из множества [math]\displaystyle{ A }[/math] ставится в соответствие элемент [math]\displaystyle{ c=a-b }[/math], называемый разностью [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math].
Вычитание возможно только, если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип).
При наличии отрицательных чисел, вычитание удобно рассматривать (и определять) как разновидность сложения — сложение с отрицательным числом[2]. К примеру, [math]\displaystyle{ 5-2=3 }[/math] можно рассматривать как сложение: [math]\displaystyle{ 5+(-2)=3 }[/math].
На множестве вещественных чисел область значений функции сложения графически имеет вид плоскости проходящей через начало координат и наклоненной к осям на 45° угловых градусов.
У вычитания есть несколько важных свойств (например для [math]\displaystyle{ A= }[/math][math]\displaystyle{ \mathbb{R} }[/math]):
- Антикоммутативность: [math]\displaystyle{ a-b = -(b-a),\quad\forall a, b \in\ A. }[/math]
- Неассоциативность: [math]\displaystyle{ (a-b)-c \ne a-(b-c),\quad\exists a, b,c \in\ A. }[/math]
- Дистрибутивность: [math]\displaystyle{ x\cdot (a-b)=(x\cdot a)-(x\cdot b),\quad\forall a, b \in\ A. }[/math]
- Вычитание [math]\displaystyle{ 0 }[/math] (нулевого элемента) даёт число равное исходному: [math]\displaystyle{ x-0=x,\quad\forall x\in A, \quad\exists 0\in A. }[/math]
В качестве примера, на картинке справа запись [math]\displaystyle{ 5-2=3 }[/math] обозначает пять яблок вычесть два яблока, что в результате дает три яблока. Заметим, что нельзя вычесть например из 5 яблок 2 груши. Помимо счета яблок, вычитание также может представлять разность других физических и абстрактных величин, таких как: отрицательные числа, дробные числа, векторы, функции, и другие.
Формы записи и терминология

Вычитание записывается с использованием символа «минус»: «[math]\displaystyle{ - }[/math]» между аргументами, такая форма записи называется инфиксной нотацией. В данном контексте символ «минус» является бинарным оператором. Результат записывается с использованием знака равенства «[math]\displaystyle{ = }[/math]», например:
- [math]\displaystyle{ a - b = c }[/math] ;
- [math]\displaystyle{ 6 - 3 = 3 }[/math] («шесть минус три равно три») ;
- [math]\displaystyle{ 64 - 35 = 29 }[/math] («шестьдесят четыре минус тридцать пять равно двадцать девять») .
На письме символ «минус» очень похож на другие письменные символы «дефис», «тире» и другие. Следует внимательнее разбирать выражение, чтобы не возникло ошибочного истолкования символа.
Свойства
Операция вычитание на числовых множествах [math]\displaystyle{ \mathbb{N}, \mathbb{Z}, \mathbb{Q}, \mathbb{R} }[/math] имеет следующие основные свойства:
- Вычитание антикоммутативно — от перемены мест аргументов разность изменяется:
- Антикоммутативность: [math]\displaystyle{ a-b \ne b-a,\quad\forall a, b \in\ A. }[/math]
- Вычитание антиассоциативно — при последовательном выполнении вычитания трёх или более чисел последовательность выполнения операций имеет значение, результат изменится:
- Антиассоциативность: [math]\displaystyle{ (a-b)-c \ne a-(b-c),\quad\forall a, b,c \in\ A. }[/math]
- Вычитание дистрибутивно, это — свойство согласованности двух бинарных операций, определённых на одном и том же множестве, также известно, как распределительный закон[4] .
- Дистрибутивность: [math]\displaystyle{ x\cdot (a-b)=(x\cdot a)-(x\cdot b),\quad\forall a, b \in\ A. }[/math]
- Относительно вычитания в множестве [math]\displaystyle{ A }[/math] существует единственный нейтральный элемент, вычитание из числа нулевого (или нейтрального элемента) даёт число равное исходному:
- Нулевой элемент: [math]\displaystyle{ x-0=x,\quad\forall x\in A, \quad\exists 0\in A. }[/math]
- Вычитание нуля идемпотентно — повторное применение операции к объекту даёт тот же результат, что и одинарное:
- Идемпотентность: [math]\displaystyle{ x = x - 0 = (x-0) - 0 = ((x-0)-0)- ... - 0,\quad\forall x\in A, \quad\exists 0\in A }[/math];
- Вычитание противоположного элемента даёт удвоенное число:
- [math]\displaystyle{ a-(-a)=a+a=2a,\quad\forall a\in A, \quad\exists -a\in A. }[/math]
Результат вычитания не всегда является определённым для множества натуральных чисел [math]\displaystyle{ \mathbb{N} }[/math]: чтобы получить натуральное число в результате вычитания, уменьшаемое должно быть больше вычитаемого. Невозможно в рамках натуральных чисел вычесть из меньшего числа большее.
Операция вычитания чисел определённых на множествах [math]\displaystyle{ \mathbb{Z}, \mathbb{Q}, \mathbb{R} }[/math] даёт число (разность) принадлежащее этому же множеству, следовательно операция вычитание относится к замкнутым операциям (операциям, не выводящим результат из данного множества чисел), то есть множества чисел [math]\displaystyle{ \mathbb{Z}, \mathbb{Q}, \mathbb{R} }[/math] образуют кольца относительно операции вычитания.
Выполнение вычитания
Операцию вычитания можно представить, как некий «черный ящик» с уменьшаемым и вычитаемым на входе и одним выходом — разностью:
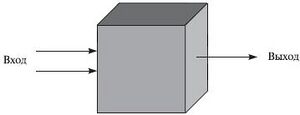
При практическом решении задачи вычитания двух чисел необходимо свести её к последовательности более простых операций: «простое вычитание», заём, сравнение и др. Для этого разработаны различные методы вычитания, например для чисел, дробей, векторов и др. На множестве натуральных чисел в настоящее время используется алгоритм поразрядного вычитания. При этом следует рассматривать вычитание как процедуру (в отличие от операции).
Как видим, процедура достаточно сложная, состоит из относительно большого числа шагов и при вычитании больших чисел может занять продолжительное время.

«Простое вычитание» — в данном контексте обозначает операцию вычитания чисел меньше двадцати, которая может быть легко сведена к декрементированию. Является гипероператором декрементирования:
[math]\displaystyle{ a-b = \operatorname{hyper-1} (a, b) = \operatorname{hyper}(a, -1, b) = a ^ {(-1)} b. }[/math]
[math]\displaystyle{ a {^{(-1)}} b = a - b = \underbrace{1 + 1 + \dots + 1}_{a} \underbrace{- 1 - 1 - \dots - 1}_{b}. }[/math]
где: [math]\displaystyle{ 1 + 1 + \dots + 1 }[/math] — последовательность операций инкрементирования, выполненная [math]\displaystyle{ a }[/math] раз;
[math]\displaystyle{ -1 - 1 - \dots - 1 }[/math] — последовательность операция декрементирования, выполненная [math]\displaystyle{ b }[/math] раз.
Чтобы упростить и ускорить процесс вычитания используют табличный метод «простого вычитания», для этого заранее вычисляют все комбинации разностей чисел от 18 до 0 и берут готовый результат из этой таблицы [5]:
| - | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||
| 2 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||
| 3 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||
| 4 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||
| 5 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||
| 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||
| 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||
| 8 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||
| 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Данная процедура применима к вычитанию натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.
Вычитание чисел
Натуральные числа
Воспользуемся определением натуральных чисел [math]\displaystyle{ \mathbb{N} }[/math] как классов эквивалентности конечных множеств. Обозначим классы эквивалентности конечных множеств [math]\displaystyle{ C, A, B }[/math] порождённых биекциями, с помощью скобок: [math]\displaystyle{ [C], [A], [B] }[/math]. Тогда арифметическая операция «вычитание» определяется следующим образом:
где [math]\displaystyle{ A \setminus B=\{C \in A \mid C \not\in B \mid B \subset A \} }[/math] — разность множеств. Данная операция на классах введена корректно, то есть не зависит от выбора элементов классов, и совпадает с индуктивным определением.
Взаимно однозначное отображение конечного множества [math]\displaystyle{ A }[/math] на отрезок [math]\displaystyle{ N_a }[/math] можно понимать как нумерацию элементов множества [math]\displaystyle{ A: \quad A \sim N_a }[/math] . Этот процесс нумерации называют «СЧЕТОМ». Таким образом, «счет» — это установление взаимно однозначного соответствия между элементами множества и отрезком натурального ряда чисел.
Для вычитания натуральных чисел в позиционной системе обозначения чисел применяется поразрядный алгоритм вычитания. Если даны два натуральных числа [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] такие, что:
где [math]\displaystyle{ a_{0 \dots n-1}=a_k P^k, \quad b_{0 \dots n-1}=b_k P^k }[/math]; [math]\displaystyle{ n }[/math] — количество цифр в числе [math]\displaystyle{ n \in \{1, 2, \dots ,n \} }[/math]; [math]\displaystyle{ k }[/math] — порядковый номером разряда (позиции), [math]\displaystyle{ k \in \{0, 1, \dots ,n-1 \} }[/math]; [math]\displaystyle{ P }[/math] — основание системы счисления; [math]\displaystyle{ \{P \} }[/math] множество числовых знаков (цифр), конкретной системы счисления: [math]\displaystyle{ \{P_2 \}= \{0,1 \} }[/math], [math]\displaystyle{ \{P_{10} \}= \{0,1,2,3,4,5,6,7,8,9 \} }[/math], [math]\displaystyle{ \{P_{16} \}= \{0,1,2,3,4,5,6,7,8,9,A,B,C,D,F \} }[/math]; тогда:
вычитая поразрядно, получаем:
- [math]\displaystyle{ c_0=\begin{cases} a_0-b_0, \quad & \text{if } a_0 \geqslant b_0 \text{ } \\ a_0+P-b_0, \quad a_1=a_1-1 & \text{if } a_0 \lt b_0 \text{ } \end{cases} }[/math]
- [math]\displaystyle{ c_1=\begin{cases} a_1-b_1, \quad & \text{if } a_1 \geqslant b_1 \text{ } \\ a_1+P-b_1, \quad a_2=a_2-1 & \text{if } a_1 \lt b_1 \text{ } \end{cases} }[/math]
- [math]\displaystyle{ ... \quad \quad... \quad \quad... }[/math]
- [math]\displaystyle{ c_{n-1}=\begin{cases} a_{n-1}-b_{n-1}, \quad & \text{if } a_{n-1}\geqslant b_{n-1} \text{ } \\ a_{n-1}+P-b_{n-1}, \quad a_n=a_n-1 & \text{if } a_{n-1}\lt b_{n-1} \text{ } \end{cases} }[/math]
Таким образом операция вычитания сводится к процедуре последовательного простого вычитания натуральных чисел [math]\displaystyle{ a_{k}-b_{k} }[/math], с формированием заёма при необходимости, которое производится либо табличным методом, либо декрементированием (счетом).
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно пользоваться таблицей вычитания, соответствующей данному основанию [math]\displaystyle{ P }[/math] системы счисления.
Пример вычитания натуральных чисел в двоичной, десятичной и шестнадцатеричной системах счисления, для удобства числа записываются друг под другом соответственно разрядам, знак заёма пишется сверху, недостающие разряды дополняются нулями:
Целые числа
Множество целых чисел — расширение множества натуральных чисел [math]\displaystyle{ \mathbb{N} }[/math], получаемое добавлением отрицательных чисел [6] вида [math]\displaystyle{ -n }[/math]. Множество целых чисел обозначается [math]\displaystyle{ \mathbb{Z}. }[/math] Арифметические операции над целыми числами определяются как непрерывное продолжение соответствующих операций над натуральными числами.
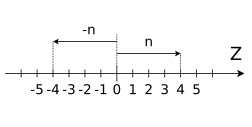
Наличие отрицательных чисел позволяет рассматривать (и определять) «вычитание» как разновидность «сложения» — сложение с отрицательным числом. Однако рассмотрим в рамках данной статьи «вычитание», как операцию определённую на множестве целых чисел, это также относится и к следующим числовым множествам. Отличие от натуральных чисел состоит в том, что отрицательные числа на числовой прямой направлены в противоположную сторону, это несколько меняет процедуру вычитания. Необходимо учитывать взаимное направление чисел, здесь возможны несколько случаев:
- Если оба аргумента положительные, тогда: [math]\displaystyle{ c = a - b; }[/math]
- Если один из аргументов отрицателен, тогда: [math]\displaystyle{ c= -a - b = -(a+b), }[/math] либо [math]\displaystyle{ c= a - (-b) = a+b; }[/math]
- Если оба аргумента отрицательны, тогда: [math]\displaystyle{ c = (-a)-(-b) = - a + b = b - a. }[/math]
Здесь и далее также используется алгоритм поразрядного вычитания (сложения). Например, рассмотрим выражение: [math]\displaystyle{ -6-4=-10 }[/math]; так как у чисел [math]\displaystyle{ -6 }[/math] и [math]\displaystyle{ 4 }[/math] разные знаки, то выносим минус за скобки: [math]\displaystyle{ -6-4=-(6+4) }[/math], вычисляя далее получим ответ: [math]\displaystyle{ -10 }[/math].
Рациональные числа
Множество рациональных чисел обозначается [math]\displaystyle{ \mathbb{Q} }[/math] (от англ. quotient «частное») и может быть записано в таком виде: [math]\displaystyle{ \mathbb{Q} = \left\{ \frac{m}{n} \mid m \in \mathbb{Z}, n \in \mathbb{N} \right\}. }[/math]
Для вычитания рациональных чисел в виде обыкновенных (или простых) дробей вида: [math]\displaystyle{ \pm \frac{m}{n} }[/math], их следует преобразовать (привести) к общему (одинаковому) знаменателю. Например, взять произведение знаменателей, числители при этом умножаются на соответствующие знаменатели. Затем вычесть полученные числители, а произведение знаменателей станет общим.
Если даны два рациональных числа [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] такие, что: [math]\displaystyle{ a=\frac{m_a}{n_a}, b=\frac{m_b}{n_b} \quad\forall m_a, n_a, m_b, n_b \in \mathbb{N} \quad\forall {n_a},{n_b} \ne 0 }[/math] (дроби не сокращаемые), тогда:
Либо можно найти наименьшее общее кратное (НОК) знаменателей. Порядок действий:
- Находим наименьшее общее кратное знаменателей: [math]\displaystyle{ M=[n_a,n_b] }[/math].
- Умножаем числитель и знаменатель первой дроби на [math]\displaystyle{ \frac{M}{n_a} }[/math].
- Умножаем числитель и знаменатель второй дроби на [math]\displaystyle{ \frac{M}{n_b} }[/math].
После этого знаменатели обеих дробей совпадают (равны [math]\displaystyle{ M }[/math]). В ряде простых случаев это упрощает вычисления, но в случае больших чисел расчёты значительно усложняются. Можно взять в качестве [math]\displaystyle{ M }[/math] любое другое общее кратное.
Пример вычитания:
Если знаменатели обеих дробей совпадают, то:
Если знаменатели кратны какому либо числу, то преобразуем только одну дробь:
Арифметическая операция «вычитание» над рациональными числами относится к замкнутым операциям.
Вещественные числа
Арифметические операции над вещественными числами представимых бесконечными десятичными дробями определяются как непрерывное продолжение[8] соответствующих операций над рациональными числами.
Если даны два вещественных числа, представимые бесконечными десятичными дробями:
определённые соответственно фундаментальными последовательностями рациональных чисел (удовлетворяющие условию Коши), обозначенные как: [math]\displaystyle{ \alpha = [a_n] }[/math] и [math]\displaystyle{ \beta = [b_n] }[/math], то их разностью называют число [math]\displaystyle{ \gamma = [c_n] }[/math], определённое разностью последовательностей [math]\displaystyle{ \{a_n\} }[/math] и [math]\displaystyle{ \{b_n\} }[/math]:
вещественное число [math]\displaystyle{ \gamma = \alpha - \beta }[/math], удовлетворяет следующему условию:
Таким образом разностью двух вещественных чисел [math]\displaystyle{ \alpha }[/math] и [math]\displaystyle{ \beta }[/math] является такое вещественное число [math]\displaystyle{ \gamma }[/math] которое содержится между всеми разностями вида [math]\displaystyle{ a' - b' }[/math] с одной стороны и всеми разностями вида [math]\displaystyle{ a'' - b'' }[/math] с другой стороны[9].
На практике для того, чтобы вычесть два числа [math]\displaystyle{ \alpha }[/math] и [math]\displaystyle{ \beta }[/math], необходимо заменить их с требуемой точностью приближёнными рациональными числами [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math]. За приближенное значение разности чисел [math]\displaystyle{ \alpha - \beta }[/math] берут разность указанных рациональных чисел [math]\displaystyle{ a-b }[/math]. При этом не важно, с какой стороны (по недостатку или по избытку) взятые рациональные числа приближают [math]\displaystyle{ \alpha }[/math] и [math]\displaystyle{ \beta }[/math]. Сложение производится по алгоритму поразрядного сложения.
При вычитании приближённых чисел их абсолютные погрешности складываются [math]\displaystyle{ \Delta (a - b)=\Delta a+ \Delta b }[/math], абсолютная погрешность числа принимается равной половине последнего знака этого числа. Относительная погрешность разности заключена между наибольшим и наименьшим значениями относительных погрешностей аргументов; на практике принимается наибольшее значение [math]\displaystyle{ \delta (a - b)=\max(\delta a,\delta b) }[/math]. Полученный результат округляют до первой верной значащей цифры, значащая цифра приближенного числа является верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.
Пример вычитания [math]\displaystyle{ \gamma=\pi-e }[/math], с точностью до 3-го знака после запятой:
- Округляем данные числа до 4-го знака после запятой (для повышения точности вычислений);
- Получаем: [math]\displaystyle{ \pi\approx 3.1416, \quad e \approx 2.7183 }[/math] ;
- Поразрядно вычитаем: [math]\displaystyle{ \gamma = \pi - e \approx 3.1416 - 2.7183 \approx 0.4233 }[/math] ;
- Округляем до 3-го знака после запятой: [math]\displaystyle{ \gamma\approx 0.423 }[/math] .
График
На множестве вещественных чисел область значений функции вычитания графически имеет вид плоскости проходящей через начало координат и наклоненной к осям на 45° угловых градусов.

Так как [math]\displaystyle{ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} }[/math], то и для этих множеств область значений функции вычитания будет принадлежать этой плоскости.
Комплексные числа
Множество комплексных чисел с арифметическими операциями является полем и обычно обозначается символом [math]\displaystyle{ \mathbb{C} }[/math].
Комплексные числа вычитаются друг с другом путём вычитания действительных и мнимых частей[10]. Это значит, что:
- [math]\displaystyle{ c+fi=(a+di) - (b+ei) = (a-b) + (d-e)i,\ }[/math]
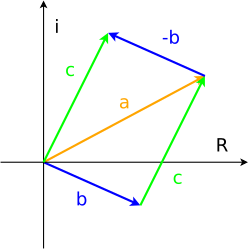
Где: [math]\displaystyle{ c, a, b, d, e, f \in \R }[/math], [math]\displaystyle{ i }[/math] — мнимая единица. Используя представление комплексных чисел как векторов на комплексной плоскости, можно дать вычитанию комплексных чисел следующую геометрическую интерпретацию: разностью комплексных чисел [math]\displaystyle{ a+di }[/math] и [math]\displaystyle{ b+ei }[/math], представленных векторами на комплексной плоскости, будет вектор, соединяющий концы уменьшаемого вектора и вычитаемого вектора и направленный от вычитаемого к уменьшаемому, он является разностью векторов и соответственно разностью комплексных чисел (аналогично будет если к уменьшаемому вектору прибавить вектор обратный вычитаемому вектору).
Аналогично для комплексных чисел n-ой размерности: [math]\displaystyle{ A=a_11+a_2i_2+ \dots +a_{n}i_n, ~~~ B=b_11+b_2i_2+ \dots +b_{n}i_n; }[/math] [math]\displaystyle{ C=A-B=(a_11+a_2i_2+ \dots +a_{n}i_n) - (b_11+b_2i_2+ \dots +b_{n}i_n) = }[/math] [math]\displaystyle{ =(a_1-b_1)1+(a_2-b_2)i_2+ \dots +(a_n-b_n)i_n = c_11+c_2i_2+ \dots +c_ni_n. }[/math]
Экспоненциальная запись
В экспоненциальной записи числа записываются в виде [math]\displaystyle{ a= \pm x \cdot P^{ \pm n} }[/math], где [math]\displaystyle{ x }[/math] — мантисса, [math]\displaystyle{ P^{n} }[/math] — характеристика числа, [math]\displaystyle{ P }[/math] — основание системы счисления. Для вычитания двух чисел, которые записаны в экспоненциальной форме, требуется, чтобы у них были одинаковые характеристики: [math]\displaystyle{ a \cdot P^{n} - b \cdot P^{n} = (a-b) \cdot P^{n}, }[/math] согласно свойству дистрибутивности.
Например:
- [math]\displaystyle{ 2.3 \cdot 10^{-5} - 5.67 \cdot 10^{-6} = 2.34 \cdot 10^{-5} - 0.567 \cdot 10^{-5} = (2.34 - 0.567) \cdot 10^{-5} = 1.773 \cdot 10^{-5} }[/math]
Вычитание произвольных чисел
При вычитании чисел принадлежащих разным множествам необходимо произвести расширение числа из множества с меньшей мощностью в сторону числа из множества с большей мощностью, либо оба числа расширить до уравнивания множеств, если существует такая возможность. Например, если нужно вычесть из рационального числа [math]\displaystyle{ 9{,}56 }[/math] натуральное число [math]\displaystyle{ 4 }[/math], то воспользовавшись тем, что натуральные числа являются подмножеством рациональных, расширяем натуральное число [math]\displaystyle{ 4 }[/math] до рационального числа [math]\displaystyle{ 4{,}00 }[/math] и вычитаем два рациональных числа [math]\displaystyle{ 9{,}56-4{,}00=5{,}56 }[/math]. Аналогично, пользуясь тем, что: [math]\displaystyle{ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C} \subset \mathbb{H} }[/math] можно вычитать числа из различных множеств между собой.
Особенности обучения вычитанию школьников
Практика показывает, что школьников легче научить вычислять разность чисел, чем научить их принимать решение о применимости операции вычитания в той или иной задаче. Это связано с тем, что вычитание, в отличие, например, от сложения, — некоммутативная операция, её аргументы играют разные роли, и ситуации задач на вычитание, которые должен разрешить ученик, существенно разнообразней, чем при сложении. В связи с этим детям, решившим задачу на вычитание одного вида, может быть затруднительно решить задачу на вычитание другого вида, даже с такими же числовыми данными. Педагог, работающий с ребёнком, должен убедиться, что его ученик уверенно чувствует себя и находит решение задач на вычитание следующих видов:
| Виды задач | Примеры задач |
| Задачи на нахождение результата действия или процесса, приводящих к уменьшению (расходу) начального количества | У Васи было 5 яблок, 3 из них он раздал друзьям. Сколько яблок у него осталось? |
| Задачи на сравнение чисел и величин, нахождение разницы, превышения, избытка | На участке дороги максимальная разрешённая скорость — 60 км/ч. Автомобиль едет по ней со скоростью 85 км/ч. На сколько водитель превышает допустимую скорость? |
| Задачи на измерение интервалов — временных и пространственных (как особый cлучай предыдущего вида задач) | В школе уроки заканчиваются в 13 часов 05 минут. Сейчас 10 часов 42 минуты. Сколько ещё ждать до конца уроков? |
| Задачи на нахождение неизвестной части совокупности (объёма) как дополнения к известной части. | В классе 25 учеников. У двоих из них — рыжий цвет волос, у восьми — каштановый, шестеро — блондинов, остальные — брюнеты. Сколько в классе брюнетов? |
| Задачи на обращение операции сложения. Восстановление первого операнда | Маша положила в копилку 25 рублей и всего у неё стало 583 рубля. Сколько денег было у Маши до этого? |
| Задачи на обращение операции сложения. Восстановление второго операнда | Одна ручка стоит 20 рублей, а ручка и блокнот стоят 50 рублей. Сколько стоит блокнот? |
| Задачи на обращение операции вычитания. Восстановление второго операнда (вычитаемого) | На дереве сидело 16 ворон. Несколько ворон улетело, а осталось 5. Сколько ворон улетело? |
См. также
Примечания
- ↑ Вычитание // Математическая энциклопедия. М.: Советская энциклопедия, 1977—1985.
- ↑ Subtraction (англ.) на сайте PlanetMath.
- ↑ Лебедев, 2003, с. 97.
- ↑ Так эти свойства называются в учебниках для младших классов
- ↑ Истомина, 2005, с. 165.
- ↑ Выгодский, 2003.
- ↑ Гусев, 1988, с. 20.
- ↑ Поскольку на множестве вещественных чисел уже введено отношение линейного порядка, то мы можем определить топологию числовой прямой: в качестве открытых множеств возьмём всевозможные объединения интервалов вида [math]\displaystyle{ \{x: \alpha \lt x \lt \beta\} }[/math]
- ↑ Ильин, 1985, с. 46.
- ↑ Конвей, 1986, с. 107.
Литература
- Ильин В.А. и др. Математический анализ. Начальный курс. (неопр.). — МГУ, 1985. — Т. 1. — 662 с.
- Эндертон Г. Элементы теории множеств = Elements of Set Theory. — Gulf Professional Publishing, 1977. — 279 с. — ISBN 0-12-238440-7.
- Барсуков А.Н. Алгебра. Учебник для 6-8 классов. (неопр.). — Просвещение, 1966. — 296 с.
- Гусев В.А., Мордкович А.Г. Математика. Справочные материалы, книга для учащихся. (неопр.). — Просвещение, 1988. — 416 с.
- Истомина Н.Б. Методика обучения математике в начальной школе: Развивающее обучение. (неопр.). — Ассоциация XXI век, 2005. — 272 с. — ISBN 5-89308-193-5.
- Выгодский М. Я. Справочник по элементарной математике (неопр.). — М.: АСТ, 2003. — ISBN 5-17-009554-6.
- В.И. Игошин. КУРС ЧИСЛОВЫХ СИСТЕМ ДЛЯ ПЕДАГОГИЧЕСКОГО ВУЗА (рус.) : статья. — Саратовский государственный университет имени Н.Г. Чернышевского, 2010.
- Кононюк А.Е. Обобщенная теория моделирования. (неопр.). — Освіта України, 2012. — Т. 2. — 548 с. — ISBN 978-966-7599-50-8.
- Тире, минус и дефис, или Черты русской типографики : [арх. 24 августа 2011] // Ководство / Артемий Лебедев. — 2003. — § 97 (15 января).
- Conway, John B. Функция одной комплексной переменной = Functions of One Complex Variable I. — Springer Science, 1986. — 322 с. — ISBN 0-387-90328-3.
