Поляризация волн

Демонстрация поляризации волн: шнур от ротора перед щелью колеблется по кругу, а за щелью до точки закрепления — линейно

Поляриза́ция волн — характеристика поперечных волн, описывающая поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны. (Характеристика поперечных волн, (в плоском пространстве) определяющая работу для вектора колеблющейся величины, который перпендикулярен направлению распространения волны).

В продольной волне поляризация возникнуть не может, так как направление колебаний в волнах этого типа всегда совпадает с направлением распространения.

Виды поляризации

Отличие волн с круговой и плоской поляризацией

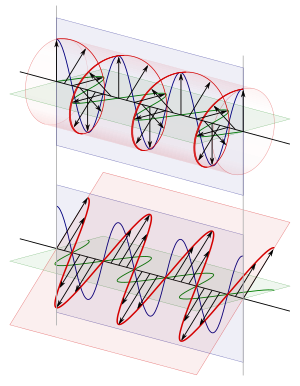
Поперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору с точностью до движения пространства. Волновой вектор показывает направление распространения волны, а вектор амплитуды показывает, в какую сторону происходят колебания. В трёхмерном пространстве имеется ещё одна степень свободы — возможность вращения вектора амплитуды вокруг волнового вектора. Тройка векторов, сопоставленная каждой точке бирегулярной кривой образует репер Френе.

Причиной возникновения поляризации волн может быть:

• несимметричная генерация волн в источнике возмущения;
• анизотропность среды распространения волн;
• преломление и отражение на границе двух сред.

Поляризация описывается фигурами Лиссажу, и соответствует сложению поперечных колебаний равной частоты (с различным сдвигом фаз). При равенстве частоты колебаний фигуры Лиссажу представляют собой эллипс, двумя крайними формами которого являются круг и отрезок прямой.

В общем случае для гармонических волн конец вектора колеблющейся величины описывает в плоскости, поперечной направлению распространения волны, эллипс: это эллиптическая поляризация. Важными частными случаями являются линейная поляризация, при которой колебания возмущения происходят в какой-то одной плоскости, в таком случае говорят о «плоско-поляризованной волне», и круговая поляризация или циркулярная поляризация, при которой конец вектора амплитуды описывает окружность в плоскости колебаний; круговая поляризация (как и эллиптическая) в зависимости от направления вращения вектора может быть положительной или правой и отрицательной или левой.

Зависимость мгновенных потенциалов при круговой поляризации

• 
• 
• 

• 

  круговая
  поляризация

• 

  эллиптическая
  поляризация

• 

  линейная
  поляризация

Поляризация электромагнитных волн

Для электромагнитных волн поляризация — явление направленного колебания векторов напряжённости электрического поля E или напряжённости магнитного поля H.

Теория явления

Электромагнитная волна может быть разложена (как теоретически, так и практически) на две поляризованные составляющие, например, поляризованные вертикально и горизонтально. Возможны другие разложения, например, по иной паре взаимно перпендикулярных направлений, или же на две составляющие, имеющие левую и правую круговую поляризацию. При попытке разложить линейно поляризованную волну по круговым поляризациям (или наоборот) возникнут две составляющие половинной интенсивности.

Как с квантовой, так и с классической точки зрения поляризация может быть описана двумерным комплексным вектором (вектором Джонса). Поляризация фотона является одной из реализаций q-бита.

Свет солнца, являющийся тепловым излучением, не имеет поляризации, однако рассеянный свет неба приобретает частичную линейную поляризацию. Поляризация света меняется также при отражении. На этих фактах основаны применения поляризующих фильтров в фотографии (например, в наблюдениях за отражающими астрономическими телами, в художественной фотографии, аэрофотосъемке или дефектоскопии) и т. д.

Линейную поляризацию имеет обычно излучение антенн.

По изменению поляризации света при отражении от поверхности можно судить о структуре поверхности, оптических постоянных, толщине образца.

Ограничить прохождение поляризованного света можно простым поворачиванием поляризационного фильтра

Если рассеянный свет поляризовать, то, используя поляризационный фильтр с иной поляризацией, можно ограничивать прохождение света. Интенсивность света, прошедшего через поляризаторы, подчиняется закону Малюса. На этом принципе работают жидкокристаллические экраны.

Некоторые живые существа, например пчёлы, способны различать линейную поляризацию света, что даёт им дополнительные возможности для ориентации в пространстве. Обнаружено, что некоторые животные, например рак-богомол, способны различать циркулярно-поляризованный свет, то есть свет с круговой поляризацией.

История открытия поляризации электромагнитных волн

Открытию поляризованных световых волн предшествовали работы многих учёных. В 1669 г. датский учёный Расмус Бартолин сообщил о своих опытах с кристаллами известкового шпата (CaCO₃), чаще всего имеющими форму правильного ромбоэдра, которые привозили возвращающиеся из Исландии моряки. Он с удивлением обнаружил, что луч света при прохождении сквозь кристалл расщепляется на два луча (называемых теперь обыкновенным и необыкновенным). Бартолин провёл тщательные исследования обнаруженного им явления двойного лучепреломления, однако объяснения ему дать не смог.

Через двадцать лет после опытов Э. Бартолина его открытие привлекло внимание нидерландского учёного Христиана Гюйгенса. Он сам начал исследовать свойства кристаллов исландского шпата и дал объяснение явлению двойного лучепреломления на основе своей волновой теории света. При этом он ввёл важное понятие оптической оси кристалла, при вращении вокруг которой отсутствует анизотропия свойств кристалла, то есть их зависимость от направления (конечно, такой осью обладают далеко не все кристаллы).

В своих опытах Гюйгенс пошёл дальше Бартолина, пропуская оба луча, вышедшие из кристалла исландского шпата, сквозь второй такой же кристалл. Оказалось, что если оптические оси обоих кристаллов параллельны, то дальнейшего разложения этих лучей уже не происходит. Если же второй ромбоэдр повернуть на 180 градусов вокруг направления распространения обыкновенного луча, то при прохождении через второй кристалл необыкновенный луч претерпевает сдвиг в направлении, противоположном сдвигу в первом кристалле, и из такой системы оба луча выйдут соединёнными в один пучок. Выяснилось также, что в зависимости от величины угла между оптическими осями кристаллов изменяется интенсивность обыкновенного и необыкновенного лучей.

Волна с круговой поляризацией.

Эти исследования вплотную подвели Гюйгенса к открытию явления поляризации света, однако решающего шага он сделать не смог, поскольку световые волны в его теории предполагались продольными. Для объяснения опытов Х. Гюйгенса И. Ньютон, придерживавшийся корпускулярной теории света, выдвинул идею об отсутствии осевой симметрии светового луча и этим сделал важный шаг к пониманию поляризации света.

В 1808 г. французский физик Этьен Луи Малюс, глядя сквозь кусок исландского шпата на блестевшие в лучах заходящего солнца окна Люксембургского дворца в Париже, к своему удивлению заметил, что при определённом положении кристалла было видно только одно изображение. На основании этого и других опытов и опираясь на корпускулярную теорию света Ньютона, он предположил, что корпускулы в солнечном свете ориентированы беспорядочно, но после отражения от какой-либо поверхности или прохождения сквозь анизотропный кристалл они приобретают определённую ориентацию. Такой «упорядоченный» свет он назвал поляризованным.

В 1810 году Малюс открыл закон, выражающий зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла между плоскостями поляризации падающего света и поляризатора. В том же году он создал количественную корпускулярную теорию поляризации света, объяснившую все известные к тому времени поляризационные явления: двойное лучепреломление света в кристаллах, закон Малюса, поляризацию при отражении и преломлении. Несколькими годами позже Био открыл вращение плоскости поляризации, которое сам же и объяснил на основе теории Малюса.

Явление поляризации считалось доказательством корпускулярной теории света и опровержением волновой теории. Но в 1815 году Ампер сказал Френелю, что поляризацию можно объяснить, предположив, что эфир совершает поперечные колебания. В 1817 году ту же гипотезу выдвинул Юнг. В 1821 году Френель создал волновую теорию поляризации света.

Поляризация монохроматических волн

В случае плоской монохроматической волны компоненты вектора [math]\displaystyle{ \vec{E} }[/math] напряжённости электрического поля (также как и компоненты вектора [math]\displaystyle{ \vec{H} }[/math] напряжённости магнитного поля) меняются совместно по гармоническому закону:

[math]\displaystyle{ \begin{cases} E_x = E_1\cos\left(\tau + \delta_1\right)\\ E_y = E_2\cos\left(\tau + \delta_2\right)\\ E_z = 0 \end{cases} }[/math]

Здесь набег фазы [math]\displaystyle{ \tau = kz-\omega t }[/math].

Поляризационный эллипс

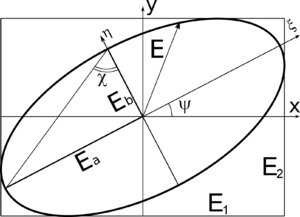
Преобразовав и сложив первые два уравнения, можно получить уравнение движения вектора [math]\displaystyle{ \vec{E} }[/math]:

[math]\displaystyle{ \left(\frac{E_x}{E_1}\right)^2 + \left(\frac{E_y}{E_2}\right)^2 - 2 \frac{E_x}{E_1}\frac{E_y}{E_2}\cos(\delta) = \sin^2{\delta} }[/math], где разность фаз [math]\displaystyle{ \delta = \delta_1-\delta_2 }[/math].

Эта квадратичная форма описывает эллипс. То есть конец вектора напряжённости плоской монохроматической волны описывает эллипс. Для того, чтобы привести её к каноническому виду, нужно повернуть эллипс на угол [math]\displaystyle{ \psi }[/math]:

[math]\displaystyle{ \begin{cases} E_\xi = E_x\cos{\psi} + E_y\sin{\psi}\\ E_\eta = - E_x\sin{\psi} + E_y\cos{\psi} \end{cases} }[/math]

Любой эллипс можно задать в параметрической форме:

[math]\displaystyle{ \begin{cases} E_\xi = E_a\cos\left(\tau + \delta\right)\\ E_\eta = E_b\sin\left(\tau + \delta\right) \end{cases} }[/math]

Здесь [math]\displaystyle{ E_a }[/math] и [math]\displaystyle{ E_b }[/math] — амплитудные значения компонент вектора [math]\displaystyle{ \vec{E} }[/math], соответствующие большой и малой полуосям эллипса. Из последних двух систем уравнений можно сделать следующий вывод:

[math]\displaystyle{ S_0 \sim E_a^2 + E_b^2 = E_1^2 + E_2^2 }[/math],

где [math]\displaystyle{ S_0 }[/math] — вектор Пойнтинга. Таким образом, в плоской монохроматической волне величина вектора Пойнтинга равна сумме потоков в двух произвольных ортогональных направлениях. Вводя обозначения [math]\displaystyle{ \mathrm{tg}\,{\alpha} = E_1 / E_2 }[/math] и [math]\displaystyle{ \mathrm{tg}\,{\chi} = E_b / E_a }[/math], из тех же двух систем уравнений можно вывести соотношения:

[math]\displaystyle{ \mathrm{tg}\,{2\psi} = -\mathrm{tg}\,{2\alpha}\cos{\delta} }[/math]

и

[math]\displaystyle{ \pm\mathrm{tg}\,{2\chi} = \sin{2\psi}\,\mathrm{tg}\,{\delta} }[/math].

С помощью последних трёх уравнений можно вычислить все параметры эллиптически поляризованной волны. А именно, зная величины [math]\displaystyle{ E_1 }[/math] и [math]\displaystyle{ E_2 }[/math] в произвольной системе координат, можно вычислить величину вектора Пойнтинга. С помощью разности фаз [math]\displaystyle{ \delta }[/math] можно определить угол поворота большой оси эллипса [math]\displaystyle{ \psi }[/math] относительно нашей системы координат, а также величины большой и малой полуосей эллипса [math]\displaystyle{ E_a }[/math] и [math]\displaystyle{ E_b }[/math].

Направление вращения вектора [math]\displaystyle{ \vec{E} }[/math] определяется разностью фаз [math]\displaystyle{ \delta }[/math]. Если [math]\displaystyle{ \sin\delta \gt 0 }[/math], тогда поляризация называется правой, а если, напротив, [math]\displaystyle{ \sin\delta \lt 0 }[/math], поляризация называется левой. В оптике (где важна плоскость изображения) если наблюдатель смотрит навстречу световому лучу, то правой поляризации соответствует движение конца вектора по часовой стрелке, а левой поляризации — против часовой стрелки. В радиофизике принято наоборот: если смотреть навстречу излучению, то вращение [math]\displaystyle{ \vec{E} }[/math] против часовой — правая поляризация, по часовой — левая. Если разность фаз равна [math]\displaystyle{ m\pi }[/math], где [math]\displaystyle{ m }[/math] — целое число, то эллипс вырождается в отрезок. Такая поляризация называется линейной. Другой важный случай возникает, когда [math]\displaystyle{ E_1 = E_2 = E }[/math] и [math]\displaystyle{ \delta = \frac{\pi}{2}\left(1+2m\right) }[/math]. В этом случае эллипс превращается в окружность, параметрическое уравнение которой имеет вид:

[math]\displaystyle{ \begin{cases} E_x = E \cos\tau \\ E_y = \pm E\cos{\left(\tau - \frac{\pi}{2}\right)} \end{cases} }[/math]

Нетрудно убедиться, что произвольная эллиптическая поляризация может быть разложена на сумму правой и левой круговых поляризаций.

Параметры Стокса

Основная статья: Параметры Стокса

Изображение поляризации языком параметров Стокса на сфере Пуанкаре

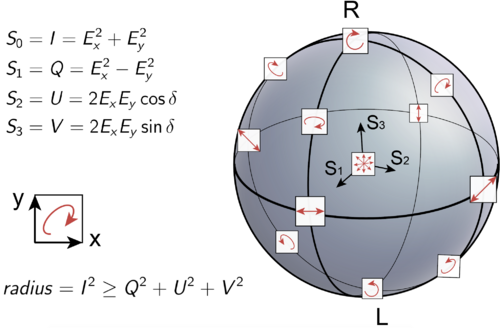
Для описания поляризации плоской монохроматической волны достаточно трёх параметров, например:

амплитуд колебаний по осям X и Y (полудлин сторон прямоугольника, в который вписан эллипс поляризации) [math]\displaystyle{ E_1 }[/math], [math]\displaystyle{ E_2 }[/math] и разностью фаз [math]\displaystyle{ \delta }[/math](между колебаниями по X и по Y), либо

полуосей эллипса [math]\displaystyle{ E_a }[/math], [math]\displaystyle{ E_b }[/math] и угла [math]\displaystyle{ \psi }[/math] между осью [math]\displaystyle{ x }[/math] и большой осью эллипса (азимутального угла эллипса или азимута, иначе называемого углом наклона эллипса). Стоксом было предложено альтернативное описание поляризации с помощью четырёх параметров, получивших его имя.

[math]\displaystyle{ S_0=E_1^2 + E_2^2 }[/math],

[math]\displaystyle{ S_1=E_1^2-E_2^2 }[/math],

[math]\displaystyle{ S_2=2E_1 E_2 \cos{\delta} }[/math],

[math]\displaystyle{ S_3=2E_1 E_2 \sin{\delta} }[/math].

Независимыми являются только три из них, ибо справедливо тождество:

[math]\displaystyle{ S^2_0=S^2_1+S^2_2+S^2_3 }[/math].

И в этом представлении для описания поляризации плоской монохроматической волны достаточно знать три параметра за исключением того, что не будет известен знак вычисляемого [math]\displaystyle{ S_1 }[/math], [math]\displaystyle{ S_2 }[/math] или [math]\displaystyle{ S_3 }[/math].

Примечание: случай частичной поляризации с [math]\displaystyle{ S^2_0\gt S^2_1+S^2_2+S^2_3 }[/math] здесь не рассматривается.

Если использовать вспомогательные углы

угол эллиптичности эллипса поляризации [math]\displaystyle{ \chi }[/math], определяемый выражением [math]\displaystyle{ \mathrm{tg}\,(\chi)=\pm E_b/E_a }[/math] (в радиофизике знак [math]\displaystyle{ + }[/math] соответствует левой, а [math]\displaystyle{ - }[/math] — правой поляризации, в оптике — наоборот), и

азимут эллипса поляризации [math]\displaystyle{ \psi }[/math], то можно получить следующие выражения для параметров Стокса:

[math]\displaystyle{ S_1=S_0 \cos (2\chi) \cos (2\psi) }[/math],

[math]\displaystyle{ S_2=S_0 \cos (2\chi) \sin (2\psi) }[/math],

[math]\displaystyle{ S_3=S_0 \sin (2\chi) }[/math].

На основе этих формул можно характеризовать поляризацию световой волны наглядным геометрическим способом. При этом параметры Стокса [math]\displaystyle{ S_1 }[/math], [math]\displaystyle{ S_2 }[/math], [math]\displaystyle{ S_3 }[/math] интерпретируются, как декартовы координаты точки, лежащей на поверхности сферы радиуса [math]\displaystyle{ S_0 }[/math]. Углы [math]\displaystyle{ 2\chi }[/math] и [math]\displaystyle{ 2\psi }[/math] имеют смысл сферических угловых координат этой точки. Такое геометрическое представление предложил Пуанкаре ^{[уточнить]}, поэтому эта сфера называется сферой Пуанкаре. В математике этой модели соответствует сфера Римана, в других разделах физики — сфера Блоха.

Наряду с [math]\displaystyle{ S_1 }[/math], [math]\displaystyle{ S_2 }[/math], [math]\displaystyle{ S_3 }[/math] используют также нормированные параметры Стокса [math]\displaystyle{ s_1=S_1/S_0 }[/math], [math]\displaystyle{ s_2=S_2/S_0 }[/math], [math]\displaystyle{ s_3=S_3/S_0 }[/math]. Для поляризованного света [math]\displaystyle{ s^2_1+s^2_2+s^2_3=1 }[/math].

s- и p-поляризации волн

Подробнее смотрите Формулы Френеля.

В оптике и электродинамике s-поляризованная волна (сравните нем. senkrecht — перпендикулярный) имеет вектор электрического поля E, перпендикулярный плоскости падения. s-поляризованную волну также называют σ-поляризованной, сагиттально поляризованной, волной E-типа, TE-волной (Transverse Electric). p-поляризованная волна (сравните лат. parallel — параллельный) имеет вектор электрического поля E, параллельный плоскости падения. p-поляризованную волну также называют π-поляризованной, поляризованной в плоскости падения, волной H-типа, TM-волной (Transverse Magnetic).

Термины TM-волна и TE-волна в работах ряда авторов меняются местами. Дело в том, что классически плоская граница предполагает однородность структуры в двух направлениях. В этом случае определяют плоскость падения и перпендикулярность напряжённостей по отношению к ней. Разделение электромагнитного поля на два несвязанных решения возможно в более общем случае структуры, однородной в одном направлении. В этом случае удобно определять перпендикулярность напряжённостей по отношению к направлению однородности. Распространение последнего определения на частный классический случай приводит к тому, что напряжённость, перпендикулярная к направлению однородности, оказывается в плоскости падения. Отмечается, что в случае металлической поверхности существенны только волны с электрической напряжённостью, перпендикулярной к границе металла. Такие волны также удобнее называть TE-волнами. Термины TM и TE связаны также с обозначением поперечных мод в лазерном резонаторе или волноводе.

В сейсмологии p-волна (от англ. primary — первичный) — продольная волна, приходящая от эпицентра землетрясения первой. s-волна (от англ. secondary — вторичный) — поперечная волна (shear wave), имеющая меньшую скорость распространения, чем продольная, и поэтому приходящая от эпицентра позднее.

Практическое значение

Левое изображение снято без фильтра, правое — через поляризационный фильтр

Скорость распространения волны может зависеть от её поляризации.

Две волны, линейно поляризованные под прямым углом друг к другу, не интерферируют.

Чаще всего это явление используется для создания различных оптических эффектов, а также в 3D-кинематографе (технология IMAX), где поляризация используется для разделения изображений, предназначенных правому и левому глазу.

Круговая поляризация применяется в антеннах космических линий связи, так как для приёма сигнала не важно положение плоскости поляризации передающей и приёмной антенн. То есть вращение космического аппарата не повлияет на возможность связи с ним. Направление вращения круговой поляризации космической приемопередающей антенны должно совпадать с направлением вращения наземной приёмопередающей антенны, работающей с космической. То же самое с антеннами линейной поляризации. В космической связи используется поляризационная развязка, то есть на одной частоте работают антенны противоположных направлений вращения поляризации или ортогональные с линейной поляризацией.

Антенну круговой поляризации выполнить сложнее, чем антенну линейной поляризации, для этого нужен поляризатор. Антенну с поляризацией правого направления вращения легко переделать в левого направления вращения. Для этого нужно повернуть на 90 градусов относительно оси вращения её поляризатор. Вообще, круговая поляризация — вещь теоретическая. На практике говорят об антеннах эллиптической поляризации — с левым или правым направлением вращения.

Круговая поляризация света используется также в технологиях стереокинематографа RealD и MasterImage. Эти технологии подобны IMAX с той разницей, что круговая поляризация вместо линейной позволяет сохранять стереоэффект и избегать двоения изображения при небольших боковых наклонах головы.

Поляризация волн находит применение в поляризационной голографии.

Поляризация частиц

Аналогичный эффект наблюдается при квантовомеханическом рассмотрении пучка частиц, обладающих спином. Состояние отдельной частицы в этом случае, вообще говоря, не является чистым и должно описываться соответствующей матрицей плотности. Для частицы со спином ½ (скажем, электрона) это эрмитова матрица 2×2 [math]\displaystyle{ \rho^a_b }[/math] со следом 1:

[math]\displaystyle{ \rho_{ab} = \rho^\dagger_{ab} = \bar \rho_{ba} }[/math]

[math]\displaystyle{ \mathrm{tr}\, \rho^a_b = 1 }[/math]

В общем случае она имеет вид

[math]\displaystyle{ \rho^a_b = {1\over 2} (\delta^a_b + 2 \hat {\sigma}^a_b \bar {s}) }[/math]

Здесь [math]\displaystyle{ \hat {\sigma} = (\sigma_x,\sigma_y,\sigma_z) }[/math] — вектор, составленный из матриц Паули, а [math]\displaystyle{ \bar{s} }[/math] — вектор среднего спина частицы. Величина

[math]\displaystyle{ \rho = 2 |\bar{s}| = 2 \sqrt{s_x^2 + s_y^2 + s_z^2} }[/math]

называется степенью поляризации частицы. Это вещественное число [math]\displaystyle{ 0\lt \rho\lt 1. }[/math] Значение [math]\displaystyle{ \rho =1 }[/math] соответствует полностью поляризованному пучку частиц, при этом

[math]\displaystyle{ \rho^a_b = \psi^a \otimes \psi^\dagger_b }[/math]

где [math]\displaystyle{ \psi }[/math] — вектор состояния частицы. Фактически, полностью поляризованные частицы можно полностью описать вектором состояния.

См. также

• Поляризатор
• Двойное лучепреломление
• Морская радиополяриметрия
• Эффект Умова
• Матрица Мюллера

Литература

• Борн М., Вольф Э. Основы оптики. Изд. 2-е. — М.: «Наука», 1973. — 720 с.
• Жаров А. А., Смирнов А. И. Поляризация волн // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — С. 65. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
• Фейнман Р., Лейтон Р., Сэндс М. Электродинамика // Фейнмановские лекции по физике. — М.: «Мир», 1965. — Т. 6.
• Какичашвили Ш. Д. Поляризационная голография / отв. ред. Ю. Н. Денисюк. — Л.: «Наука», 1989. — 141 с.