Интерференция волн

Картина интерференции большого количества круговых когерентных волн, в зависимости от длины волны и расстояния между источниками

Интерференция волн (лат. interferens, от inter — между + -ferens — несущий, переносящий) — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга^[1]. Сопровождается чередованием максимумов (пучностей) и минимумов (узлов) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.

Интерферировать могут все волны, однако устойчивая интерференционная картина будет наблюдаться только в том случае, если волны имеют одинаковую частоту и колебания в них не ортогональны. Интерференция может быть стационарной и нестационарной. Стационарную интерференционную картину могут давать только полностью когерентные волны. Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников, при интерференции дадут результирующую волну, фронтом которой будет сфера.

При интерференции энергия волн перераспределяется в пространстве^[1]. Это не противоречит закону сохранения энергии, потому что в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн^[2].

При наложении некогерентных волн средняя величина квадрата амплитуды (то есть интенсивность результирующей волны) равна сумме квадратов амплитуд (интенсивностей) накладывающихся волн. Энергия результирующих колебаний каждой точки среды равна сумме энергий её колебаний, обусловленных всеми некогерентными волнами в отдельности.

Именно отличие результирующей интенсивности волнового процесса от суммы интенсивностей его составляющих и есть признак интерференции^[3].

Расчёт результата сложения двух сферических волн

Интерференция волн от двух точечных когерентных источников сферических волн. Синим и красным/желтым обозначены минимумы и максимумы

Если в некоторой однородной и изотропной среде два точечных источника возбуждают сферические волны, то в произвольной точке пространства M может происходить наложение волн в соответствии с принципом суперпозиции (наложения): каждая точка среды, куда приходят две или несколько волн, принимает участие в колебаниях, вызванных каждой волной в отдельности. Таким образом волны не взаимодействуют друг с другом и распространяются независимо друг от друга.

Две одновременно распространяющиеся синусоидальные сферические волны [math]\displaystyle{ s_1 }[/math] и [math]\displaystyle{ s_2 }[/math], созданные точечными источниками B₁ и B₂, вызовут в точке M колебание, которое, по принципу суперпозиции, описывается формулой [math]\displaystyle{ s=s_1+s_2 }[/math]. Согласно формуле сферической волны:

[math]\displaystyle{ s_1={A_1 \over r_1}\sin(\omega_1 t - k_1r_1 + \alpha_1)={A_1 \over r_1}\sin \Phi_1 }[/math],

[math]\displaystyle{ s_2={A_2 \over r_2}\sin(\omega_2 t - k_2r_2 + \alpha_2)={A_2 \over r_2}\sin \Phi_2 }[/math],

где

[math]\displaystyle{ \Phi_1=\omega_1 t - k_1r_1 + \alpha_1 }[/math] и [math]\displaystyle{ \Phi_2=\omega_2 t - k_2r_2 + \alpha_2 }[/math] — фазы распространяющихся волн

[math]\displaystyle{ k_1 }[/math] и [math]\displaystyle{ k_2 }[/math] — волновые числа ([math]\displaystyle{ k={\omega \over v}={2\pi \over \lambda} }[/math])

[math]\displaystyle{ \omega_1 }[/math] и [math]\displaystyle{ \omega_2 }[/math] — циклические частоты каждой волны

[math]\displaystyle{ \alpha_1 }[/math] и [math]\displaystyle{ \alpha_2 }[/math] — начальные фазы,

[math]\displaystyle{ r_1 }[/math] и [math]\displaystyle{ r_2 }[/math] — расстояния от точки М до точечных источников B₁ и B₂

В результирующей волне [math]\displaystyle{ s=s_1+s_2={A \over r}\sin \Phi }[/math], амплитуда [math]\displaystyle{ {A \over r} }[/math] и фаза [math]\displaystyle{ \Phi }[/math] определяются формулами:

[math]\displaystyle{ {A \over r}=\sqrt{\left({A_1 \over r_1}\right)^2 + \left({A_2 \over r_2}\right)^2 + 2{A_1 \over r_1}{A_2 \over r_2}\cos(\Phi_2-\Phi_1)} }[/math],

[math]\displaystyle{ \Phi=\operatorname{arctg}{ {{A_1 \over r_1}\sin\Phi_1 + {A_2 \over r_2}\sin\Phi_2} \over {{A_1 \over r_1}\cos\Phi_1 + {A_2 \over r_2}\cos\Phi_2} } }[/math]

Условием интерференции является когерентность двух волн. Волны и возбуждающие их источники когерентны, если разность фаз волн [math]\displaystyle{ \Phi_2-\Phi_1 }[/math] не зависит от времени. Если разность фаз волн [math]\displaystyle{ \Phi_2-\Phi_1 }[/math] изменяется с течением времени, то такие волны некогерентны. В формуле для разности фаз только первый член зависит от времени:

[math]\displaystyle{ \Phi_2-\Phi_1=(\omega_2-\omega_1)t-(k_2r_2-k_1r_1)+(\alpha_2-\alpha_1) }[/math], где [math]\displaystyle{ k_1={\omega_1 \over v} }[/math], [math]\displaystyle{ k_2={\omega_2 \over v} }[/math],

[math]\displaystyle{ v }[/math] — скорость распространения волны в данной среде. Таким образом, две синусоидальные волны когерентны, если их частоты одинаковы ([math]\displaystyle{ \omega_1=\omega_2 }[/math]), и некогерентны, если условие не выполняется. Для когерентных волн ([math]\displaystyle{ \omega_1=\omega_2=\omega }[/math]) при условии [math]\displaystyle{ \alpha_2-\alpha_1=0 }[/math] разность фаз равна:

[math]\displaystyle{ \Phi_2-\Phi_1=-{\omega \over v}(r_2-r_1)=-k(r_2-r_1) }[/math].

Амплитуда колебаний в результирующей волне максимальна [math]\displaystyle{ \left({A \over r}={A_1 \over r_1}+{A_2 \over r_2}\right) }[/math] во всех точках среды, для которых

[math]\displaystyle{ k(r_2-r_1)=2m\pi }[/math], где [math]\displaystyle{ m=0, \pm 1, \pm 2, ... }[/math](m-целое), или

[math]\displaystyle{ r_2-r_1=m\lambda }[/math], (так как [math]\displaystyle{ k={2\pi \over \Delta} }[/math]).

Величина [math]\displaystyle{ r_2-r_1=\Delta }[/math] называется геометрической разностью хода волн от их источников B₁ и B₂, до рассматриваемой точки среды.

Амплитуда колебаний в результирующей волне минимальна [math]\displaystyle{ \left({A \over r}= \begin{vmatrix}{A_1 \over r_1}-{A_2 \over r_2} \end{vmatrix} \right) }[/math] во всех точках среды, для которых

[math]\displaystyle{ k(r_2-r_1)=(2m-1)\pi }[/math], где [math]\displaystyle{ m=1, 2,... }[/math] (m-натуральное), или

[math]\displaystyle{ \Delta=r_2-r_1=(2m-1){\lambda \over 2} }[/math].

При наложении когерентных волн квадрат амплитуды и энергия результирующей волны отличаются от суммы квадратов амплитуд и суммы энергий накладываемых волн.

Между двумя плоскими волнами

Простая форма интерференционной картины получается, если две плоские волны одинаковой частоты пересекаются под углом. Интерференция — это, по сути, процесс перераспределения энергии. Энергия, потерянная при деструктивной интерференции, восстанавливается при конструктивной интерференции. Пусть одна волна движется горизонтально, а другая движется под углом θ к первой волне. Если предположить, что две волны находятся в фазе в точке B, тогда относительная фаза изменяется вдоль оси x. Разность фаз в точке A определяется выражением

[math]\displaystyle{ \Delta \varphi = \frac {2 \pi d} {\lambda} = \frac {2 \pi x \sin \theta} {\lambda}. }[/math]

Видно, что две волны находятся в фазе при условии

[math]\displaystyle{ \frac {x \sin \theta} {\lambda} = 0, \pm 1, \pm 2, \ldots , }[/math]

и не совпадают по фазе на половине периода, когда

[math]\displaystyle{ \frac {x \sin \theta} {\lambda} = \pm \frac {1}{2}, \pm \frac {3}{2}, \ldots }[/math]

Конструктивная интерференция возникает, когда волны находятся в фазе, а деструктивная интерференция — когда они не совпадают по фазе на половине периода. Таким образом, создается картина интерференционных полос, где расстояние между максимумами равно

[math]\displaystyle{ d_f = \frac {\lambda} {\sin \theta} }[/math]

и d_f — расстояние между полосами. Расстояние между полосами увеличивается с увеличением длины волны и уменьшением угла θ .

Полосы наблюдаются там, где две волны перекрываются, а расстояние между полосами одинаково.

Несколько лучей

Интерференция также возникает, когда несколько волн складываются вместе при условии, что разность фаз между ними остается постоянной в течение времени наблюдения.

Иногда желательно, чтобы несколько волн одной частоты и амплитуды подавлялись до исчезновения (то есть деструктивно интерферировали). На этом принципе основаны, например, трехфазное питание и дифракционная решетка. В обоих случаях результат достигается за счет равномерного распределения фаз.

Легко видеть, что амплитуда набора волн исчезает, если они имеют одинаковую амплитуду и их фазы разнесены по углам. Используя векторы, каждую волну можно представить как [math]\displaystyle{ A e^{i \varphi_n} }[/math] для [math]\displaystyle{ N }[/math] волны от [math]\displaystyle{ n=0 }[/math] к [math]\displaystyle{ n = N-1 }[/math], где

[math]\displaystyle{ \varphi_n - \varphi_{n-1} = \frac{2\pi}{N}. }[/math]

Чтобы показать это

[math]\displaystyle{ \sum_{n=0}^{N-1} A e^{i \varphi_n} = 0 }[/math]

можно просто предположить обратное, а затем обе части умножить на [math]\displaystyle{ e^{i \frac{2\pi}{N}}. }[/math]

Интерферометр Фабри — Перо использует интерференцию между многократно отражёнными лучами.

Дифракционную решетку можно рассматривать как многолучевой интерферометр; поскольку пики, которые она создаёт, генерируются интерференцией между светом, пропускаемым каждым из элементов решетки; см. « Интерференция против дифракции» для дальнейшего обсуждения.

Оптическая интерференция

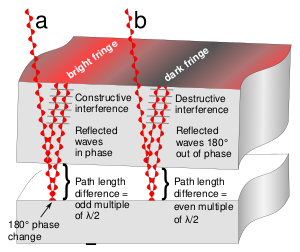
Поскольку частота световых волн (~ 10¹⁴ Гц) слишком высока для обнаружения доступными в настоящее время детекторами, можно наблюдать только интенсивность оптической интерференционной картины. Интенсивность света в данной точке пропорциональна квадрату средней амплитуды волны. Математически это выражается следующим образом. Смещение двух волн в точке r равно:

[math]\displaystyle{ U_1 (\mathbf r,t) = A_1(\mathbf r) e^{i [\varphi_1 (\mathbf r) - \omega t]} }[/math]

[math]\displaystyle{ U_2 (\mathbf r,t) = A_2(\mathbf r) e^{i [\varphi_2 (\mathbf r) - \omega t]} }[/math]

где A представляет собой величину смещения, φ — фаза, а ω — угловая частота.

Смещение суммируемых волн равно

[math]\displaystyle{ U (\mathbf r,t) = A_1(\mathbf r) e^{i [\varphi_1 (\mathbf r) - \omega t]}+A_2(\mathbf r) e^{i [\varphi_2 (\mathbf r) - \omega t]}. }[/math]

Интенсивность света в точке r определяется интегралом

[math]\displaystyle{ I(\mathbf r) = \int U (\mathbf r,t) U^* (\mathbf r,t) \, dt \propto A_1^2 (\mathbf r)+ A_2^2 (\mathbf r) + 2 A_1 (\mathbf r) A_2 (\mathbf r) \cos [\varphi_1 (\mathbf r)-\varphi_2 (\mathbf r)]. }[/math]

Его можно выразить через интенсивности отдельных волн как

[math]\displaystyle{ I(\mathbf r) = I_1 (\mathbf r)+ I_2 (\mathbf r) + 2 \sqrt{ I_1 (\mathbf r) I_2 (\mathbf r)} \cos [\varphi_1 (\mathbf r)-\varphi_2 (\mathbf r)]. }[/math]

Таким образом, интерференционная картина отображает разность фаз между двумя волнами с максимумами, возникающими, когда разность фаз кратна 2π. Если два луча имеют одинаковую интенсивность, то максимумы в четыре раза ярче, чем отдельные лучи, а минимумы имеют нулевую интенсивность.

Две волны должны иметь одинаковую поляризацию, чтобы вызвать интерференционные полосы, поскольку волны с разными поляризациями не могут подавлять друг друга или усиливаться. Вместо этого, когда волны с разной поляризацией складываются, они порождают волну с другим состоянием поляризации.

Требования к источнику света

Приведенное выше обсуждение предполагает, что интерферирующие друг с другом волны являются монохроматическими, то есть имеют одну частоту — для этого требуется, чтобы они были бесконечными во времени. Однако это не является ни практичным, ни необходимым. Две идентичные волны конечной длительности, частота которых фиксирована в течение этого периода, при наложении вызовут интерференционную картину. Две идентичные волны, которые состоят из узкого спектра частотных волн конечной длительности (но короче, чем время их когерентности), дадут серию полос со слегка различающимися промежутками, и при условии, что разброс промежутков значительно меньше, чем средний промежуток между полосами. Картина полос будет наблюдаться при перекрытии двух волн.

Обычные источники света излучают волны разной частоты и в разное время из разных точек источника. Если свет разделить на два фронта волны, а затем повторно объединить, то каждая отдельная световая волна может генерировать интерференционную картину со своей другой половиной, но сгенерированные отдельные полосы будут иметь разные фазы и интервалы, и, как правило, не будет наблюдаться общего узора полос. Однако одноэлементные источники света, такие как натриевые или ртутные лампы, имеют линии излучения с довольно узкими частотными спектрами. Если их пространственно и по цвету отфильтровать, а затем разделить на две волны, то они могут быть наложены друг на друга для создания интерференционных полос^[4]. Вся интерферометрия до изобретения лазера проводилась с использованием таких источников и имела широкий спектр применений.

Лазерный луч обычно гораздо ближе приближается к монохроматическому источнику, и, таким образом, его гораздо проще использовать для генерации интерференционных полос. Легкость, с которой интерференционные полосы можно наблюдать с помощью лазерного луча, иногда может вызывать проблемы, поскольку паразитные отражения могут давать ложные интерференционные полосы, которые могут приводить к ошибкам.

Обычно в интерферометрии используется один лазерный луч, хотя интерференция наблюдалась с использованием двух независимых лазеров, частоты которых были достаточно согласованы, чтобы удовлетворить требованиям фазы^[5]. Она также наблюдалась для широкопольной интерференции между двумя некогерентными лазерными источниками^[6].

Также возможно наблюдение интерференционных полос с использованием белого света. Узор полос белого света можно рассматривать как составленный из «спектра» узоров полос, каждый из которых имеет немного разный интервал. Если все узоры полос находятся в фазе в центре, то полосы будут увеличиваться в размере по мере уменьшения длины волны, а суммарная интенсивность покажет от трех до четырёх полос разного цвета. Янг описал этот эффект в своем обсуждении двухщелевого опыта. Поскольку полосы белого света получаются только тогда, когда две волны прошли равные расстояния от источника света, то они оказываются очень полезны в интерферометрии, поскольку позволяют идентифицировать полосу нулевой разности хода^[7].

Оптические устройства

Для создания интерференционных полос, свет от источника нужно разделить на две волны, которые затем должны быть повторно объединены. Традиционно интерферометры классифицируются как системы с разделением по амплитуде или с разделением волнового фронта.

В системе с разделением амплитуды светоделитель используется для разделения света на два луча, движущихся в разных направлениях, которые затем накладываются друг на друга для создания интерференционной картины. Интерферометр Майкельсона и интерферометр Маха — Цендера служат распространёнными примерами систем с разделением амплитуды.

В системах с разделением волнового фронта, волна разделена в пространстве, как демонстрируется в двухщелевом интерферометре Юнга и зеркале Ллойда.

Интерференцию также можно увидеть в повседневных явлениях, таких как радужность и структурная окраска. Например, цвета, видимые в мыльном пузыре, возникают из-за интерференции света, отражающегося от передней и задней поверхностей тонкой мыльной пленки. В зависимости от толщины пленки возникают интерференционные полосы разных цветов.

Приложения

Оптическая интерферометрия

Интерферометрия сыграла важную роль в развитии физики, а также имеет широкий спектр приложений в метрологии.

Двухщелевой интерферометр Томаса Юнга в 1803 г. продемонстрировал интерференционные полосы, когда два маленьких отверстия освещались светом из другого маленького отверстия, освещенным солнечным светом. Янг смог оценить длину волны разных цветов в спектре по расстоянию между интерференционными полосами. Эксперимент сыграл важную роль в принятии волновой теории света^[7]. В квантовой механике считается, что этот эксперимент демонстрирует неразделимость волновой и частичной природы света и других квантовых частиц (дуальность волна-частица). Ричард Фейнман любил говорить, что вся квантовая механика может быть получена путем тщательного обдумывания последствий этого единственного эксперимента^[8].

Результаты эксперимента Майкельсона — Морли обычно приводятся как первые убедительные доказательства против теории светоносного эфира в пользу специальной теории относительности.

Интерферометрия использовалась для определения и калибровки стандартов длины. Когда метр был определён как расстояние между двумя отметками на платино-иридиевом стержне, Майкельсон и Бенуа использовали интерферометрию для измерения длины волны красной линии кадмия в новом стандарте, а также показали, что его можно использовать в качестве стандарта длины. Шестьдесят лет спустя, в 1960 году, метр в новой системе СИ определили как равный 1 650 763,73 длинам волн оранжево-красной эмиссионной линии в электромагнитном спектре атома криптона-86 в вакууме. Это определение заменили в 1983 году определением метра как расстояния, пройденного светом в вакууме за определённый промежуток времени. Интерферометрия по-прежнему играет важную роль в создании калибровочного инструмента при измерении длин.

Интерферометрия используется при калибровке датчиков скольжения (называемых в США мерными блоками) и в координатно-измерительных машинах. Она используется при тестировании оптических компонент^[9].

Радиоинтерферометрия

Очень большая антенная решетка — это интерферометрическая решетка, состоящая из множества меньших телескопов, как и многие большие радиотелескопы, работающие в режиме интерферометра.

В 1946 году была разработана методика, получившая название астрономической интерферометрии. Астрономические радиоинтерферометры обычно состоят либо из решеток параболических антенн, либо из двумерных решеток всенаправленных антенн. Все телескопы в группе широко разнесены и обычно соединяются вместе с помощью коаксиального кабеля, волновода, оптического волокна или другой линии передачи. Интерферометрия увеличивает общий собираемый сигнал, но её основная цель — значительно увеличить разрешение с помощью процесса, называемого синтезом апертуры. Этот метод работает путем наложения (интерференции) сигнальных волн от разных телескопов по принципу, согласно которому волны, совпадающие с одной и той же фазой, складываются друг с другом, в то время как две волны с противоположными фазами нейтрализуют друг друга. Это создает комбинированный телескоп, который по разрешению (но не по чувствительности) эквивалентен одиночной антенне, диаметр которой равен расстоянию между антеннами, наиболее удаленными друг от друга в решетке.

Акустическая интерферометрия

Акустический интерферометр — это инструмент для измерения физических характеристик звуковых волн в газе или жидкости, таких как скорость, длина волны, поглощение или импеданс. Вибрирующий кристалл создает ультразвуковые волны, которые излучаются в среду. Волны падают на отражатель, расположенный параллельно кристаллу, затем отражаются обратно к источнику и измеряются.

Квантовая интерференция

Квантовая интерференция сильно отличается от классической волновой интерференции, описанной выше, и ниже приводятся важные отличия. Однако квантовая интерференция похожа на оптическую интерференцию.

Пусть [math]\displaystyle{ \Psi (x, t) }[/math] — волновая функция решение уравнения Шредингера для квантовомеханического объекта. Тогда вероятность [math]\displaystyle{ P(x) }[/math] наблюдения объекта в координате [math]\displaystyle{ x }[/math] записывается[math]\displaystyle{ P(x) = |\Psi (x, t)|^2 = \Psi^* (x, t) \Psi (x, t) }[/math], где * обозначает комплексное сопряжение. При квантовой интерференции обсуждается поведение волновой функции, выражаемой как сумма или линейная суперпозиция двух членов [math]\displaystyle{ \Psi (x, t) = \Psi_A (x, t) + \Psi_B (x, t) }[/math] или точнее возникающей вероятности

[math]\displaystyle{ P(x) = |\Psi (x, t)|^2 = |\Psi_A (x, t)|^2 + |\Psi_B (x, t)|^2 + (\Psi_A^* (x, t) \Psi_B (x, t) + \Psi_A (x, t) \Psi_B^* (x, t)) }[/math]

Обычно, [math]\displaystyle{ \Psi_A (x, t) }[/math] и [math]\displaystyle{ \Psi_B (x, t) }[/math] соответствуют различным состояниям A и B. В этом случае уравнение [math]\displaystyle{ \Psi (x, t) = \Psi_A (x, t) + \Psi_B (x, t) }[/math] указывает на то, что объект может находиться в состоянии A или B. Приведенное выше уравнение можно интерпретировать как: Вероятность обнаружения объекта в точке [math]\displaystyle{ x }[/math], вероятность нахождения объекта в точке [math]\displaystyle{ x }[/math], когда он находится в состоянии A, плюс вероятность найти объект в точке [math]\displaystyle{ x }[/math], когда он находится в состоянии B, плюс дополнительный член. Этот дополнительный член, который называется квантовым интерференционным членом, равен [math]\displaystyle{ \Psi_A^* (x, t) \Psi_B (x, t) + \Psi_A (x, t) \Psi_B^* (x, t) }[/math] в приведенном выше уравнении. Как и в случае с классической волной, описанном выше, член квантовой интерференции может складываться (конструктивная интерференция) или вычитаться (деструктивная интерференция) из [math]\displaystyle{ |\Psi_A (x, t)|^2 + |\Psi_B (x, t)|^2 }[/math] в приведенном выше уравнении в зависимости от того, является ли член квантовой интерференции положительным или отрицательным. Если это слагаемое отсутствует для всех [math]\displaystyle{ x }[/math], то квантово-механическая интерференция, связанная с состояниями A и B, отсутствует.

Самый известный пример квантовой интерференции — эксперимент с двумя щелями. В этом эксперименте электроны, атомы или другие квантово-механические объекты приближаются к барьеру с двумя прорезями. Если квантовому объекту удается пройти через щели, его положение измеряется детекторным экраном на определённом расстоянии за барьером. Для этой системы можно сквазать, что [math]\displaystyle{ \Psi_A (x, t) }[/math] — часть волновой функции, которая проходит через одну из щелей и [math]\displaystyle{ \Psi_B (x, t) }[/math] — частью волновой функции, которая проходит через другую щель. Когда объект почти достигает экрана, вероятность того, где он находится, определяется приведенным выше уравнением. В этом контексте уравнение гласит, что вероятность найти объект в некоторой точке непосредственно перед тем, как он попадет на экран, — это вероятность, которая была бы получена, если бы он прошел через первую щель, плюс вероятность, которая была бы получена, если бы он прошел через вторую щель плюс квантовый интерференционный член, которому нет аналогов в классической физике. Член квантовой интерференции может значительно изменить картину, наблюдаемую на экране.

Разделение [math]\displaystyle{ \Psi_A (x, t) + \Psi_B (x, t) }[/math] особенно ясно в формулировке квантовой механике через интегралы по траекториям в контексте эксперимента с двумя щелями. [math]\displaystyle{ \Psi_A (x, t) }[/math] состоит из вкладов интеграла по траекториям, в которых траектории проходят через первую щель; [math]\displaystyle{ \Psi_B (x, t) }[/math] состоит из вкладов интегралов по траекториям, в которых они проходят через вторую щель.

Здесь список некоторых различий между классической интерференцией волн и квантовой интерференцией:

(a) при классической интерференции интерферируют две разные волны; а в квантовой интерференции - волновая функция интерферирует сама с собой.
(b) Классическая интерференция получается простым сложением сдвигов фаз двух волн, а в квантовой интерференции эффект возникает для функции вероятности, связанной с волновой функцией, и, следовательно, для абсолютного значения волновой функции возведённой в квадрат.
(c) Интерференция включает в себя различные типы математических функций: классическая волна - это действительная функция, представляющая сдвиг фаз; квантовая волновая функция - сложная функция. Классическая волна в любой точке может быть положительной или отрицательной; квантовая функция вероятности неотрицательна.

См. также

Примечания

↑ ^1,0 ^1,1 Н. С. Степанов. Интерференция волн // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия (т. 1—2); Большая Российская энциклопедия (т. 3—5), 1988—1999. — ISBN 5-85270-034-7.
↑ Г. С. Горелик. Колебания и волны,Физматгиз, 1959,гл. XI
↑ Г. С. Ландсберг. Оптика. М.,1976 г.,928 стр.с илл.
↑ Steel, W. H. Interferometry. — Cambridge : Cambridge University Press, 1986. — ISBN 0-521-31162-4.
↑ Pfleegor (1967). «Interference of independent photon beams». Phys. Rev. 159 (5): 1084–1088. doi:10.1103/physrev.159.1084. Bibcode: 1967PhRv..159.1084P.
↑ Patel (2014). «Widefield two laser interferometry». Optics Express 22 (22): 27094–27101. doi:10.1364/OE.22.027094. PMID 25401860. Bibcode: 2014OExpr..2227094P.
↑ ^7,0 ^7,1 Born, Max. Principles of Optics / Max Born, Emil Wolf. — Cambridge : Cambridge University Press, 1999. — ISBN 0-521-64222-1.
↑ Greene, Brian. The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. — New York : W.W. Norton, 1999. — ISBN 978-0-393-04688-5.
↑ RS Longhurst, Geometrical and Physical Optics, 1968, Longmans, London.

Литература

Яворский Б. М., Селезнев Ю. А., Справочное руководство по физике., М., Наука., 1984

Ссылки

* Демонстрации по интерференции света

[FE-1] 1,0 ^1,1 Н. С. Степанов. Интерференция волн // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия (т. 1—2); Большая Российская энциклопедия (т. 3—5), 1988—1999. — ISBN 5-85270-034-7.

[Колебания_и_волны-2] Г. С. Горелик. Колебания и волны,Физматгиз, 1959,гл. XI

[Ландсберг.Оптика-3] Г. С. Ландсберг. Оптика. М.,1976 г.,928 стр.с илл.

[4] Steel, W. H. Interferometry. — Cambridge : Cambridge University Press, 1986. — ISBN 0-521-31162-4.

[5] Pfleegor (1967). «Interference of independent photon beams». Phys. Rev. 159 (5): 1084–1088. doi:10.1103/physrev.159.1084. Bibcode: 1967PhRv..159.1084P.

[6] Patel (2014). «Widefield two laser interferometry». Optics Express 22 (22): 27094–27101. doi:10.1364/OE.22.027094. PMID 25401860. Bibcode: 2014OExpr..2227094P.

[Born_and_Wolf-7] 7,0 ^7,1 Born, Max. Principles of Optics / Max Born, Emil Wolf. — Cambridge : Cambridge University Press, 1999. — ISBN 0-521-64222-1.

[Greene_1999-8] Greene, Brian. The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. — New York : W.W. Norton, 1999. — ISBN 978-0-393-04688-5.

[9] RS Longhurst, Geometrical and Physical Optics, 1968, Longmans, London.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]