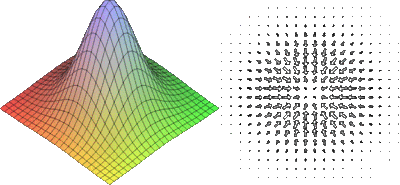
Градиент

Эта статья о векторе; о способе заливки см. Градиент (компьютерная графика).

Операция градиента преобразует холм (слева), если смотреть на него сверху, в поле векторов (справа). Видно, что векторы направлены «в горку» и чем длиннее, тем круче наклон.

Градие́нт (от лат. gradiens, род. п. gradientis «шагающий, растущий») — вектор, своим направлением указывающий направление возрастания (а антиградиент - убывания) некоторой скалярной величины [math]\displaystyle{ \varphi, }[/math] (значение которой меняется от одной точки пространства к другой, образуя скалярное поле), а по величине (модулю) равный скорости роста этой величины в этом направлении.

Например, если взять в качестве [math]\displaystyle{ \varphi }[/math] высоту поверхности земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.

Другими словами, градиент — это производная по пространству, но в отличие от производной по одномерному времени, градиент является не скаляром, а векторной величиной.

С математической точки зрения на градиент можно смотреть как на:

1. Коэффициент линейности изменения значения функции многих переменных от изменения значения аргумента;
2. Вектор в пространстве области определения скалярной функции многих переменных, составленный из частных производных;
3. Строки матрицы Якоби содержат градиенты составных скалярных функций из которых состоит векторная функция многих переменных.

Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным (безразмерным).

Термин впервые появился в метеорологии, а в математику был введён Максвеллом в 1873 г.; обозначение [math]\displaystyle{ \mathrm{grad} }[/math] тоже предложил Максвелл.

Стандартные обозначения:

[math]\displaystyle{ \mathrm{grad}\,\varphi }[/math]

или, с использованием оператора набла,

[math]\displaystyle{ \nabla \varphi }[/math]

— вместо [math]\displaystyle{ \varphi }[/math] может быть любое скалярное поле, обозначенное любой буквой, например [math]\displaystyle{ \mathrm{grad}\, V, \nabla V }[/math] — обозначения градиента поля: [math]\displaystyle{ V }[/math].

Ознакомление

Градиент 2D функции отображен на графике в виде синих стрелок

Пусть температура в комнате задана с помощью скалярного поля T таким образом, что в каждой точке, заданной координатами (x, y, z) температура равняется T(x, y, z) (предположим, что температура не изменяется с течением времени). В каждой точке комнаты градиент функции T будет показывать направление, в котором температура возрастает быстрее всего. Величина градиента определяет, насколько быстро температура возрастает в данном направлении.

Определение

Для случая трёхмерного пространства градиентом дифференцируемой в некоторой области скалярной функции [math]\displaystyle{ \varphi = \varphi(x,y,z) }[/math] координат [math]\displaystyle{ x }[/math], [math]\displaystyle{ y }[/math], [math]\displaystyle{ z }[/math] называется векторная функция с компонентами

[math]\displaystyle{ \frac {\partial \varphi} {\partial x}, \frac {\partial \varphi} {\partial y}, \frac {\partial \varphi} {\partial z}. }[/math]

Или, использовав для единичных векторов по осям прямоугольных декартовых координат [math]\displaystyle{ \vec e_x, \vec e_y, \vec e_z }[/math]:

[math]\displaystyle{ \mathrm{grad}\,\varphi = \nabla \varphi = \frac {\partial \varphi} {\partial x} \vec e_x + \frac {\partial \varphi} {\partial y} \vec e_y + \frac {\partial \varphi} {\partial z} \vec e_z. }[/math]

Если [math]\displaystyle{ \varphi }[/math] — функция [math]\displaystyle{ n }[/math] переменных [math]\displaystyle{ x_1,\;\ldots,\;x_n }[/math], то её градиентом называется [math]\displaystyle{ n }[/math]-мерный вектор

[math]\displaystyle{ \left(\frac{\partial \varphi}{\partial x_1},\;\ldots,\;\frac{\partial \varphi}{\partial x_n}\right), }[/math]

компоненты которого равны частным производным [math]\displaystyle{ \varphi }[/math] по всем её аргументам.

• Размерность вектора градиента определяется, таким образом, размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идёт речь.
• Оператором градиента называется оператор, действие которого на скалярную функцию (поле) даёт её градиент. Этот оператор иногда коротко называют просто «градиентом».

Смысл градиента любой скалярной функции [math]\displaystyle{ f }[/math] в том, что его скалярное произведение с бесконечно малым вектором перемещения [math]\displaystyle{ d\mathbf{x} }[/math] даёт полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена [math]\displaystyle{ f }[/math], то есть линейную (в случае общего положения она же главная) часть изменения [math]\displaystyle{ f }[/math] при смещении на [math]\displaystyle{ d\mathbf{x} }[/math]. Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:

[math]\displaystyle{ df = \frac {\partial f} {\partial x_1}\,dx_1 + \frac {\partial f} {\partial x_2}\,dx_2 + \frac {\partial f} {\partial x_3}\,dx_3 + \ldots = \sum_i \frac {\partial f} {\partial x_i}\,dx_i = (\mathrm{grad}\,\mathbf{f} \cdot d\mathbf x). }[/math]

Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат [math]\displaystyle{ x_i }[/math], то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку [math]\displaystyle{ d\mathbf{x} }[/math] — это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе. Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как:

[math]\displaystyle{ d f = \sum_i (\partial_i f)\,dx^i }[/math]

или, опуская по правилу Эйнштейна знак суммы,

[math]\displaystyle{ df=(\partial_i f)\,dx^i }[/math]

(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.

Используя интегральную теорему

[math]\displaystyle{ \iiint\limits_{V}\nabla\varphi\,dV=\iint\limits_{S} \varphi\,d\mathbf{s} }[/math],

градиент можно выразить в интегральной форме:

[math]\displaystyle{ \nabla\varphi=\lim\limits_{V \to 0}\frac{1}{V}\left(\iint\limits_{S} \varphi\,d\mathbf{s}\right), }[/math]

здесь [math]\displaystyle{ \it{S} }[/math] — замкнутая поверхность охватывающая объём [math]\displaystyle{ \it{V}, d\mathbf{s} }[/math] — нормальный элемент этой поверхности.

Пример

Например, градиент функции [math]\displaystyle{ \varphi(x,\;y,\;z)=2x+3y^2-\sin z }[/math] будет представлять собой:

[math]\displaystyle{ \nabla \varphi = \left(\frac{\partial \varphi}{\partial x},\;\frac{\partial \varphi}{\partial y},\;\frac{\partial \varphi}{\partial z}\right)=(2,\;6y,\;-\cos z). }[/math]

В физике

В различных отраслях физики используется понятие градиента различных физических полей.

Например, напряжённость электростатического поля есть минус градиент электростатического потенциала, напряжённость гравитационного поля (ускорение свободного падения) в классической теории гравитации есть минус градиент гравитационного потенциала. Консервативная сила в классической механике есть минус градиент потенциальной энергии.

В естественных науках

Понятие градиента находит применение не только в физике, но и в смежных и даже сравнительно далёких от физики науках (иногда это применение носит количественный, а иногда и просто качественный характер).

Например, градиент концентрации — нарастание или уменьшение по какому-либо направлению концентрации растворённого вещества, градиент температуры — увеличение или уменьшение по какому-то направлению температуры среды и т. д.

Градиент таких величин может быть вызван различными причинами, например, механическим препятствием, действием электромагнитных, гравитационных или других полей или различием в растворяющей способности граничащих фаз.

В экономике

В экономической теории понятие градиента используется для обоснования некоторых выводов. В частности, используемые для нахождения оптимума потребителя метод множителей Лагранжа и условия Куна-Таккера (позаимствованные из естественных наук) основаны на сопоставлении градиентов функции полезности и функции бюджетного ограничения.

Геометрический смысл

Рассмотрим семейство линий уровня функции [math]\displaystyle{ \varphi }[/math]:

[math]\displaystyle{ \gamma(h)=\{(x_1,\;\ldots,\;x_n)\mid \varphi(x_1,\;\ldots,\;x_n)=h\}. }[/math]

Нетрудно показать, что градиент функции [math]\displaystyle{ \varphi }[/math] в точке [math]\displaystyle{ \vec{x}{\,}^0 }[/math] перпендикулярен её линии уровня, проходящей через эту точку. Модуль градиента показывает максимальную скорость изменения функции в окрестности [math]\displaystyle{ \vec{x}{\,}^0 }[/math], то есть частоту линий уровня. Например, линии уровня высоты изображаются на топографических картах, при этом модуль градиента показывает крутизну спуска или подъёма в данной точке.

Связь с производной по направлению

Используя правило дифференцирования сложной функции, нетрудно показать, что производная функции [math]\displaystyle{ \varphi }[/math] по направлению [math]\displaystyle{ \vec{e}=(e_1,\;\ldots,\;e_n) }[/math] равняется скалярному произведению градиента [math]\displaystyle{ \varphi }[/math] на единичный вектор [math]\displaystyle{ \vec{e} }[/math]:

[math]\displaystyle{ \frac{\partial \varphi}{\partial \vec e}=\frac{\partial \varphi} {\partial x_1} e_1+\ldots+\frac{\partial \varphi}{\partial x_n} e_n = (\nabla \varphi,\;\vec e). }[/math]

Таким образом, для вычисления производной скалярной функции векторного аргумента по любому направлению достаточно знать градиент функции, то есть вектор, компоненты которого являются её частными производными.

Градиент в ортогональных криволинейных координатах

[math]\displaystyle{ \operatorname{grad}\,U(q_1,\;q_2,\;q_3) = \frac{1}{H_1}\frac{\partial U}{\partial q_1}\vec{e}_1 + \frac{1}{H_2}\frac{\partial U}{\partial q_2}\vec{e}_2 + \frac{1}{H_3}\frac{\partial U}{\partial q_3}\vec{e}_3, }[/math]

где [math]\displaystyle{ H_i }[/math] — коэффициенты Ламе.

Полярные координаты (на плоскости)

Коэффициенты Ламе:

[math]\displaystyle{ \begin{matrix}H_1 = 1 \\ H_2 = r \end{matrix}. }[/math]

Отсюда:

[math]\displaystyle{ \operatorname{grad}\,U(r,\;\theta) = \frac{\partial U}{\partial r}\vec {e_r} + \frac{1}{r}\frac{\partial U}{\partial \theta }\vec {e_\theta}. }[/math]

Цилиндрические координаты

Коэффициенты Ламе:

[math]\displaystyle{ \begin{matrix}H_1 = 1 \\ H_2 = r \\ H_3 = 1 \end{matrix}. }[/math]

Отсюда:

[math]\displaystyle{ \operatorname{grad}\,U(r,\;\theta,\;z) = \frac{\partial U}{\partial r}\vec {e_r} + \frac{1}{r}\frac{\partial U}{\partial \theta}\vec {e_\theta} + \frac{\partial U}{\partial z}\vec {e_z}. }[/math]

Сферические координаты

Коэффициенты Ламе:

[math]\displaystyle{ \begin{matrix}H_1 = 1 \;\;\;\;\;\; \\H_2 = r\;\;\;\;\;\; \\H_3 = r\sin{\theta}\end{matrix} . }[/math]

Отсюда:

[math]\displaystyle{ \operatorname{grad}\,U(r,\;\theta,\;\varphi) = \frac{\partial U}{\partial r}\vec {e_r} + \frac{1}{r}\frac{\partial U}{\partial \theta }\vec {e_\theta} + \frac{1}{r\sin{\theta}}\frac{\partial U}{\partial\varphi}\vec {e_\varphi}. }[/math]

Вариации и обобщения

• Пусть [math]\displaystyle{ u\colon X\to Y }[/math] — отображение между метрическими пространствами. Борелева функция [math]\displaystyle{ \rho\colon X\to \R }[/math] называется верхним градиентом [math]\displaystyle{ u }[/math] если следующее неравенство

  [math]\displaystyle{ |u(p)-u(q)|_Y\le \int\limits_\gamma \rho }[/math]

выполняется для произвольной спрямляемой кривой [math]\displaystyle{ \gamma }[/math], соединяющей [math]\displaystyle{ p }[/math] и [math]\displaystyle{ q }[/math] в [math]\displaystyle{ X }[/math].

См. также

• Что такое градиент на YouTube
• Векторный анализ
• Теорема Остроградского — Гаусса
• Формулы векторного анализа
• Оператор набла
• Градиент концентрации
• 4-градиент
• Оператор Кэнни
• Градиентные методы

Литература

• Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия методы и приложения: учебное пособие для физико-математических специальностей университетов. — М.: Наука, 1986. — 759 с.

Ссылки

• Броунов П. И. Градиент // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.