p-адическое число

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
(перенаправлено с «P-адические числа»)

p-адическое число[1] — теоретико-числовое понятие, определяемое для заданного фиксированного простого числа p как элемент расширения поля рациональных чисел. Это расширение является пополнением поля рациональных чисел относительно p-адической нормы, определяемой на основе свойств делимости целых чисел на p.

p-адические числа были введены Куртом Гензелем в 1897 году[2].

Поле p-адических чисел обычно обозначается [math]\displaystyle{ \mathbb Q_p }[/math] или [math]\displaystyle{ \mathbf Q_p }[/math].

Алгебраическое построение

Целые p-адические числа

Стандартное определение

Целым p-адическим числом для заданного простого p называется[3] бесконечная последовательность [math]\displaystyle{ x=\{x_1,x_2,\ldots\} }[/math] вычетов [math]\displaystyle{ x_n }[/math] по модулю [math]\displaystyle{ p^{n} }[/math], удовлетворяющих условию:

[math]\displaystyle{ x_n\equiv x_{n+1}\pmod{p^n}. }[/math]

Сложение и умножение целых p-адических чисел определяется как почленное сложение и умножение таких последовательностей. Для них непосредственно проверяются все аксиомы кольца. Кольцо целых p-адических чисел обычно обозначается [math]\displaystyle{ \mathbb{Z}_p }[/math].

Определение через проективный предел

В терминах проективных пределов кольцо целых [math]\displaystyle{ p }[/math]-адических чисел определяется как предел

[math]\displaystyle{ \lim_{\leftarrow}\mathbb{Z} / {p^n}\mathbb{Z} }[/math]

колец [math]\displaystyle{ \mathbb{Z} / {p^n}\mathbb{Z} }[/math] вычетов по модулю [math]\displaystyle{ p^n }[/math] относительно естественных проекций [math]\displaystyle{ \mathbb{Z}/{p^{n+1}}\mathbb{Z} \to \mathbb{Z}/{p^n}\mathbb{Z} }[/math].

Эти рассмотрения можно провести в случае не только простого числа [math]\displaystyle{ p }[/math], но и любого составного числа [math]\displaystyle{ m }[/math] — получится т. н. кольцо [math]\displaystyle{ m }[/math]-адических чисел, но это кольцо в отличие от [math]\displaystyle{ \mathbb{Z}_p }[/math] обладает делителями нуля, поэтому дальнейшие построения, рассматриваемые ниже, к нему неприменимы.

Свойства

Обычные целые числа вкладываются в [math]\displaystyle{ \mathbb{Z}_p }[/math] очевидным образом: [math]\displaystyle{ x=\{x,x,\ldots\} }[/math] и являются подкольцом.

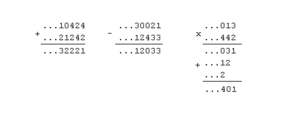
Пример выполнения арифметических операций над 5-адическими числами.

Беря в качестве элемента класса вычетов число [math]\displaystyle{ a_n = x_n\,\bmod\,{p^n} }[/math] (таким образом, [math]\displaystyle{ 0\le a_n\lt p^n }[/math]), мы можем записать каждое целое p-адическое число в виде [math]\displaystyle{ x=\{a_1,a_2,\ldots\} }[/math] однозначным образом. Такое представление называется каноническим. Записывая каждое [math]\displaystyle{ a_n }[/math] в p-ичной системе счисления [math]\displaystyle{ a_n=b_n\ldots b_2b_1 }[/math] и, учитывая, что [math]\displaystyle{ a_n\equiv a_{n+1}\pmod{p^n} }[/math], возможно всякое p-адическое число в каноническом виде представить в виде [math]\displaystyle{ x=\{b_1, b_2b_1, b_3b_2b_1,\ldots\} }[/math] или записать в виде бесконечной последовательности цифр в p-ичной системе счисления [math]\displaystyle{ x=\{\ldots b_n\ldots b_2b_1\} }[/math]. Действия над такими последовательностями производятся по обыкновенным правилам сложения, вычитания и умножения «столбиком» в p-ичной системе счисления.

В такой форме записи натуральным числам и нулю соответствуют p-адические числа с конечным числом ненулевых цифр, совпадающих с цифрами исходного числа. Отрицательным числам соответствуют p-адические числа с бесконечным числом ненулевых цифр, например в пятеричной системе −1=…4444=(4).

p-адические числа

Определение как поля частных

p-адическим числом называется элемент поля частных [math]\displaystyle{ \mathbb{Q}_p }[/math] кольца [math]\displaystyle{ \mathbb{Z}_p }[/math] целых p-адических чисел. Это поле называется полем p-адических чисел.

Свойства

Поле p-адических чисел содержит в себе поле рациональных чисел.

Пример выполнения деления 5-адических чисел.

Нетрудно доказать, что любое целое p-адическое число, не кратное p, обратимо в кольце [math]\displaystyle{ \mathbb{Z}_p }[/math], а кратное p однозначно записывается в виде [math]\displaystyle{ xp^n }[/math], где x не кратно p и поэтому обратимо, а [math]\displaystyle{ n\gt 0 }[/math]. Поэтому любой ненулевой элемент поля [math]\displaystyle{ \mathbb{Q}_p }[/math] может быть записан в виде [math]\displaystyle{ xp^n }[/math], где x не кратно p, а n любое; если n отрицательно, то, исходя из представления целых p-адических чисел в виде последовательности цифр в p-ичной системе счисления, мы можем записать такое p-адическое число в виде последовательности [math]\displaystyle{ x=\{\ldots b_k\ldots b_2b_1,b_0b_{-1}\ldots b_{n+1}\} }[/math], то есть, формально представить в виде p-ичной дроби с конечным числом цифр после запятой и, возможно, бесконечным числом ненулевых цифр до запятой. Деление таких чисел можно также производить аналогично «школьному» правилу, но начиная с младших, а не старших разрядов числа.

Метрическое построение

Любое рациональное число [math]\displaystyle{ r }[/math] можно представить как [math]\displaystyle{ r=p^n\frac ab }[/math] где [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] целые числа, не делящиеся на [math]\displaystyle{ p }[/math], а [math]\displaystyle{ n }[/math] — целое. Тогда [math]\displaystyle{ |r|_p }[/math] — [math]\displaystyle{ p }[/math]-адическая норма [math]\displaystyle{ r }[/math] — определяется как [math]\displaystyle{ p^{-n} }[/math]. Если [math]\displaystyle{ r=0 }[/math], то [math]\displaystyle{ |r|_p=0 }[/math].

Поле [math]\displaystyle{ p }[/math]-адических чисел есть пополнение поля рациональных чисел с метрикой [math]\displaystyle{ d_p }[/math], определённой [math]\displaystyle{ p }[/math]-адической нормой: [math]\displaystyle{ d_p(x,y)=|x-y|_p }[/math]. Это построение аналогично построению поля вещественных чисел как пополнения поля рациональных чисел при помощи нормы, являющейся обычной абсолютной величиной.

Норма [math]\displaystyle{ |r|_p }[/math] продолжается по непрерывности до нормы на [math]\displaystyle{ \mathbb{Q}_p }[/math].

Свойства

  • Каждый элемент x поля p-адических чисел может быть представлен в виде сходящегося ряда
[math]\displaystyle{ x=\sum_{i=n_0}^\infty a_ip^i }[/math]
где [math]\displaystyle{ n_0 }[/math] — некоторое целое число, а [math]\displaystyle{ a_i }[/math] — целые неотрицательные числа, не превосходящие [math]\displaystyle{ p-1 }[/math]. А именно, в качестве [math]\displaystyle{ a_i }[/math] здесь выступают цифры из записи x в системе счисления с основанием p. Такая сумма всегда сходится в метрике [math]\displaystyle{ d_p }[/math] к самому [math]\displaystyle{ x }[/math].
[math]\displaystyle{ |x-z|_p\le\max\left\{|x-y|_p,|y-z|_p\right\}. }[/math]
  • Числа [math]\displaystyle{ x\in \mathbb Q_p }[/math] с условием [math]\displaystyle{ |x|_p\le 1 }[/math] образуют кольцо [math]\displaystyle{ \mathbb{Z}_p }[/math] целых p-адических чисел, являющееся пополнением кольца целых чисел [math]\displaystyle{ \mathbb{Z}\subset \mathbb{Q} }[/math] в норме [math]\displaystyle{ |x|_p }[/math].
  • Числа [math]\displaystyle{ x\in \mathbb{Q}_p }[/math] с условием [math]\displaystyle{ |x|_p= 1 }[/math] образуют мультипликативную группу и называются p-адическими единицами.
  • Совокупность чисел [math]\displaystyle{ x\in \mathbb{Q}_p }[/math] с условием [math]\displaystyle{ |x|_p\lt 1 }[/math] является главным идеалом в [math]\displaystyle{ \mathbb{Z}_p }[/math] с образующим элементом p.
  • Метрическое пространство [math]\displaystyle{ (\mathbb{Z}_p,d_p) }[/math] гомеоморфно канторову множеству, а пространство [math]\displaystyle{ (\mathbb{Q}_p,d_p) }[/math] гомеоморфно канторову множеству с вырезанной точкой.
  • Для различных p нормы [math]\displaystyle{ |x|_p }[/math] независимы, а поля [math]\displaystyle{ \mathbb{Q}_p }[/math] неизоморфны.
  • Для любых элементов [math]\displaystyle{ r_\infty }[/math], [math]\displaystyle{ r_2 }[/math], [math]\displaystyle{ r_3 }[/math], [math]\displaystyle{ r_5 }[/math], [math]\displaystyle{ r_7 }[/math], … таких, что [math]\displaystyle{ r_\infty \in \mathbb R }[/math] и [math]\displaystyle{ r_p\in \mathbb Q_p }[/math], можно найти последовательность рациональных чисел [math]\displaystyle{ x_n }[/math] таких, что для любого p выполнено [math]\displaystyle{ |x_i-r_p|_p\to 0 }[/math] и [math]\displaystyle{ |x_i-r_\infty|\to 0 }[/math].

Применения

  • Если [math]\displaystyle{ F(x_1,x_2,\ldots,x_n) }[/math] — многочлен с целыми коэффициентами, то разрешимость при всех [math]\displaystyle{ k }[/math] сравнения
[math]\displaystyle{ F(x_1,x_2,\cdots,x_n)\equiv 0 \pmod{p^k} }[/math]
эквивалентна разрешимости уравнения
[math]\displaystyle{ F(x_1,x_2,\cdots,x_n) = 0 }[/math]
в целых [math]\displaystyle{ p }[/math]-адических числах. Необходимым условием разрешимости этого уравнения в целых или рациональных числах является его разрешимость в кольцах или, соответственно, полях [math]\displaystyle{ p }[/math]-адических чисел при всех [math]\displaystyle{ p }[/math], а также в поле вещественных чисел. Для некоторых классов многочленов (например, для квадратичных форм) это условие является также достаточным.
На практике для проверки разрешимости уравнения в целых [math]\displaystyle{ p }[/math]-адических числах достаточно проверить разрешимость указанного сравнения для определенного конечного числа значений [math]\displaystyle{ k }[/math]. Например, согласно лемме Гензеля, при [math]\displaystyle{ n=1 }[/math] достаточным условием для разрешимости сравнения при всех натуральных [math]\displaystyle{ k }[/math] служит наличие простого решения у сравнения по модулю [math]\displaystyle{ p }[/math] (то есть, простого корня у соответствующего уравнения в поле вычетов по модулю [math]\displaystyle{ p }[/math]). Иначе говоря, при [math]\displaystyle{ n=1 }[/math] для проверки наличия корня у уравнения в целых [math]\displaystyle{ p }[/math]-адических числах, как правило, достаточно решить соответствующее сравнение при [math]\displaystyle{ k=1 }[/math].
  • [math]\displaystyle{ p }[/math]-адические числа находят широкое применение в теоретической физике[4]. Известны [math]\displaystyle{ p }[/math]-адические обобщённые функции[5], p-адический аналог оператора дифференцирования (оператор Владимирова)[6], p-адическая квантовая механика[7][8], p-адическая спектральная теория[9], p-адическая теория струн[10][11]

См. также

Примечания

  1. ↑ Произносится: пэ-адическое; соответственно: два-адическое, три-адическое и т. п.
  2. ↑ Kurt Hensel. Über eine neue Begründung der Theorie der algebraischen Zahlen // Jahresbericht der Deutschen Mathematiker-Vereinigung. — 1897. — Т. 6, № 3. — С. 83—88. (нем.)
  3. ↑ Боревич З. И., Шафаревич И. Р. Теория чисел, 1985, с. 25—28..
  4. ↑ Vladimiriv V. S., Volovich I. V., Zelenov E. I. P-adic analysis and mathematical physics // Singapure: World Sci., 1993
  5. ↑ Владимиров В. С. «Обобщённые функции над полем p-адических чисел» // УМН, 1988, т. 43 (5), с. 17-53
  6. ↑ Владимиров В. С. О спектральных свойствах p-адических псевдодифференциальных операторов типа Шредингера // Изв. РАН, Сер. мат., 1992, т. 56, с. 770—789
  7. ↑ Vladimiriv V. S., Volovich I. V. P-adic quantum mechanics // Commun. Math. Phys., 1989, vol. 123, P. 659—676
  8. ↑ Vladimiriv V. S., Volovich I. V. P-adic Schrodinger-type equation // Lett. Math. Phys., 1989, vol. 18, P. 43-53
  9. ↑ Владимиров В. С., Волович И. В., Зеленов Е. И. Спектральная теория в p-адической квантовой механике и теория представлений // Изв. АН СССР, т. 54 (2), с. 275—302, (1990)
  10. ↑ Volovich I. V. P-adic string // Class. Quant. Grav., 1987, vol. 4, P. L83-L84
  11. ↑ Frampton P. H. Retrospective on p-adic string theory // Труды математического института имени В. А. Стеклова. Сборник, № 203 — М.: Наука, 1994. — isbn 5-02-007023-8 — С. 287—291.

Литература

  • Боревич З. И., Шафаревич И. Р. Теория чисел. — М.: Наука, 1985.
  • Коблиц Н. р-адические числа, р-адический анализ и дзета-функции, — М.: Мир, 1982.
  • Серр Ж.-П. Курс арифметики, — М.: Мир, 1972.
  • Беккер Б., Востоков С., Ионин Ю. 2-адические числа // Квант. — 1979. — № 2. — С. 26—31.
  • Конрад К. Введение в p-адические числа Летняя школа «Современная математика», 2014 г. Дубна
Источник — https://xn--h1ajim.xn--p1ai/index.php?title=P-адическое_число&oldid=5827265