Потоковый шифр

Пото́чный или Пото́ковый шифр — это симметричный шифр, в котором каждый символ открытого текста преобразуется в символ шифрованного текста в зависимости не только от используемого ключа, но и от его расположения в потоке открытого текста. Поточный шифр реализует другой подход к симметричному шифрованию, нежели блочные шифры.

История

Потоковые шифры на базе сдвиговых регистров активно использовались в годы войны, ещё задолго до появления электроники. Они были просты в проектировании и реализации.

В 1965 году Эрнст Селмер, главный криптограф норвежского правительства, разработал теорию последовательности сдвиговых регистров. Позже Соломон Голомб, математик Агентства Национальной Безопасности США, написал книгу под названием «Shift Register Sequences» («Последовательности сдвиговых регистров»), в которой изложил свои основные достижения в этой области, а также достижения Селмера.

Большую популярность потоковым шифрам принесла работа Клода Шеннона, опубликованная в 1949 году, в которой Шеннон доказал абсолютную стойкость шифра Вернама (также известного, как одноразовый блокнот). В шифре Вернама ключ имеет длину, равную длине самого передаваемого сообщения. Ключ используется в качестве гаммы, и если каждый бит ключа выбирается случайно, то вскрыть шифр невозможно (так как все возможные открытые тексты будут равновероятны). К настоящему времени создано большое количество алгоритмов потокового шифрования, таких как: A3, A5, A8, MUGI, PIKE, RC4, SEAL.

Режим гаммирования для поточных шифров

Режим гаммирования для поточных шифров

Простейшая реализация поточного шифра изображена на рисунке. Генератор гаммы выдаёт ключевой поток (гамму): [math]\displaystyle{ k_1,k_2,k_3,\dots ,k_L }[/math]. Обозначим поток битов открытого текста [math]\displaystyle{ m_1,m_2,m_3,\dots ,m_L }[/math]. Тогда поток битов шифротекста получается с помощью применения операции XOR: [math]\displaystyle{ c_1,c_2,c_3,\dots ,c_L }[/math], где [math]\displaystyle{ c_i=m_i\oplus k_i }[/math].

Расшифрование производится операцией XOR между той же самой гаммой и зашифрованным текстом: [math]\displaystyle{ m_i=c_i\oplus k_i }[/math].

Очевидно, что если последовательность битов гаммы не имеет периода и выбирается случайно, то взломать шифр невозможно. Но у данного режима шифрования есть и отрицательные особенности. Так ключи, сравнимые по длине с передаваемыми сообщениями, трудно использовать на практике. Поэтому обычно применяют ключ меньшей длины (например, 128 бит). С помощью него генерируется псевдослучайная гаммирующая последовательность (она должна удовлетворять постулатам Голомба). Естественно, псевдослучайность гаммы может быть использована при атаке на потоковый шифр.

Классификация потоковых шифров

Допустим, например, что в режиме гаммирования для потоковых шифров при передаче по каналу связи произошло искажение одного знака шифротекста. Очевидно, что в этом случае все знаки, принятые без искажения, будут расшифрованы правильно. Произойдёт потеря лишь одного знака текста. А теперь представим, что один из знаков шифротекста при передаче по каналу связи был потерян. Это приведёт к неправильному расшифрованию всего текста, следующего за потерянным знаком.
Практически во всех каналах передачи данных для потоковых систем шифрования присутствуют помехи. Поэтому для предотвращения потери информации решают проблему синхронизации шифрования и расшифрования текста. По способу решения этой проблемы шифросистемы подразделяются на синхронные и системы с самосинхронизацией.

Синхронные потоковые шифры

Определение:

Синхронные потоковые шифры (СПШ) — шифры, в которых поток ключей генерируется независимо от открытого текста и шифротекста.

При шифровании генератор потока ключей выдаёт биты потока ключей, которые идентичны битам потока ключей при дешифровании. Потеря знака шифротекста приведёт к нарушению синхронизации между этими двумя генераторами и невозможности расшифрования оставшейся части сообщения. Очевидно, что в этой ситуации отправитель и получатель должны повторно синхронизоваться для продолжения работы.

Обычно синхронизация производится вставкой в передаваемое сообщение специальных маркеров. В результате этого пропущенный при передаче знак приводит к неверному расшифрованию лишь до тех пор, пока не будет принят один из маркеров.

Заметим, что выполняться синхронизация должна так, чтобы ни одна часть потока ключей не была повторена. Поэтому переводить генератор в более раннее состояние не имеет смысла.

Плюсы СПШ:

• отсутствие эффекта распространения ошибок (только искажённый бит будет расшифрован неверно);
• предохраняют от любых вставок и удалений шифротекста, так как они приведут к потере синхронизации и будут обнаружены.

Минусы СПШ:

• уязвимы для изменения отдельных бит шифрованного текста. Если злоумышленнику известен открытый текст, он может изменить эти биты так, чтобы они расшифровывались, как ему надо.

Самосинхронизирующиеся потоковые шифры

Основная статья: Самосинхронизирующийся потоковый шифр

Основная идея построения была запатентована в 1946 г. в США.

Определение:

Самосинхронизирующиеся потоковые шифры (асинхронные потоковые шифры (АПШ)) — шифры, в которых ключевой поток создаётся функцией ключа и фиксированного числа знаков шифротекста.

Итак, внутреннее состояние генератора потока ключей является функцией предыдущих N битов шифротекста. Поэтому расшифрующий генератор потока ключей, приняв N битов, автоматически синхронизируется с шифрующим генератором.

Реализация этого режима происходит следующим образом: каждое сообщение начинается случайным заголовком длиной N битов; заголовок шифруется, передаётся и расшифровывается; расшифровка является неправильной, зато после этих N бит оба генератора будут синхронизированы.

Плюсы АПШ:

• Размешивание статистики открытого текста. Так как каждый знак открытого текста влияет на следующий шифротекст, статистические свойства открытого текста распространяются на весь шифротекст. Следовательно, АПШ может быть более устойчивым к атакам на основе избыточности открытого текста, чем СПШ.

Минусы АПШ:

• распространение ошибки (каждому неправильному биту шифротекста соответствуют N ошибок в открытом тексте);
• чувствительны к вскрытию повторной передачей.

Потоковые шифры на регистрах сдвига с линейной обратной связью (РСЛОС)

Теоретическая основа

Есть несколько причин использования линейных регистров сдвига в криптографии:

• высокое быстродействие криптографических алгоритмов
• применение только простейших операций сложения и умножения, аппаратно реализованных практически во всех вычислительных устройствах
• хорошие криптографические свойства (генерируемые последовательности имеют большой период и хорошие статистические свойства)
• легкость анализа с использованием алгебраических методов за счет линейной структуры

Определение: Регистр сдвига с линейной обратной связью длины L состоит из L ячеек пронумерованных [math]\displaystyle{ 0,1,2,\dots L-1 }[/math],каждая из которых способна хранить 1 бит и имеет один вход и один выход; и синхросигнала (clock), который контролирует смещение данных. В течение каждой единицы времени выполняются следующие операции:

• содержимое ячейки [math]\displaystyle{ L-1 }[/math] формирует часть выходной последовательности;
• содержимое [math]\displaystyle{ i }[/math]-той ячейки перемещается в ячейку [math]\displaystyle{ i+1 }[/math] для любого [math]\displaystyle{ i }[/math], [math]\displaystyle{ 0\le i\lt L-1 }[/math].
• новое содержимое ячейки [math]\displaystyle{ 0 }[/math] определяется битом обратной связи, который вычисляется сложением по модулю 2 с определёнными коэффициентами битов ячеек [math]\displaystyle{ 0,1,2,\dots L-1 }[/math].

Регистр сдвига с линейной обратной связью.

На первом шаге: [math]\displaystyle{ S_L=c_1 \cdot S_{L-1}\oplus c_2 \cdot S_{L-2}\oplus \dots \oplus c_L \cdot S_0. }[/math]

На втором шаге: [math]\displaystyle{ S_{L+1}=c_1 \cdot S_L\oplus c_2 \cdot S_{L-1}\oplus \dots \oplus c_L \cdot S_1. }[/math]

Следующее соотношение описывает в общем виде работу РСЛОС:

[math]\displaystyle{ S_j=c_1 \cdot S_{j-1}\oplus c_2 \cdot S_{j-2}\oplus \dots\oplus c_L \cdot S_{j-L}. }[/math]
Если мы запишем во все ячейки биты равны нулю, то система будет генерировать последовательность, состоящую из всех нулей. Если записать ненулевые биты, то получим полубесконечную последовательность. Последовательность определяется коэффициентами [math]\displaystyle{ c_1,c_2,\dots ,c_L. }[/math]
Посмотрим, каким может быть период [math]\displaystyle{ T }[/math] такой системы:
Число ненулевых заполнений:[math]\displaystyle{ 2^L-1. }[/math] Значит, [math]\displaystyle{ T\leqslant 2^L-1 }[/math].
После возникновения одного заполнения, которое было раньше, процесс начнёт повторяться. Процесс заполнения регистра, как показано выше, представим линейным разностным уравнением. Перенесём все члены в одну часть равенства, получим:
[math]\displaystyle{ S_{j}\oplus c_{1}\cdot S_{j-1}\oplus c_{2}\cdot S_{j-2}\oplus\dots\oplus c_{L}\cdot S_{j-L}=0 }[/math].

Обозначим: [math]\displaystyle{ S_j=D^{-j} }[/math]. Тогда:
[math]\displaystyle{ (1 \oplus c_1\cdot D \oplus c_2\cdot D^2 \oplus \dots \oplus c_L\cdot D^L )\cdot D^{-j}. }[/math]

[math]\displaystyle{ C(D) = 1 \oplus c_1\cdot D \oplus c_2 \cdot D^2 \oplus \dots \oplus c_L\cdot D^L. }[/math]

Важным свойством этого многочлена является - приводимость.
Определение:
Многочлен называется приводимым, если он может быть представлен как произведение двух многочленов меньших степеней с коэффициентами из данного поля (в нашем случае с двоичными коэффициентами). Если такое представление не имеет место, то многочлен называется неприводимым.
Если многочлен [math]\displaystyle{ C(D) }[/math] является неприводимым и примитивным, то период будет совпадать с максимально возможным периодом, равным [math]\displaystyle{ 2^L-1. }[/math]

Пример.

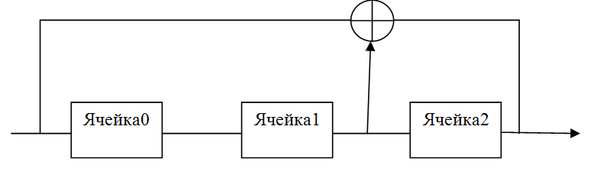
Пример: Возьмём неприводимый примитивный многочлен [math]\displaystyle{ C(D)=D^3+D^2+1 (c_3=1, c_2=1,c_1=0). }[/math] Этот многочлен можно записать, как [math]\displaystyle{ (3,2,0) }[/math] – выписаны степени, при которых стоят ненулевые коэффициенты.
Запишем в исходном состоянии в ячейки [math]\displaystyle{ 0 0 1 }[/math] и определим длину периода генератора:

Таблица. Определение периода генератора

Обратная связь	Ячейка0	Ячейка1	Ячейка2
1	0	0	1
0	1	0	0
1	0	1	0
1	1	0	1
1	1	1	0
0	1	1	1
0	0	1	1
1	0	0	1

Период генератора равен [math]\displaystyle{ 7 (2^3-1=7). }[/math] На выходе генератора буде последовательность: [math]\displaystyle{ 1001011 1001011 1001011\dots }[/math]
Приведём примеры некоторых примитивных многочленов по модулю 2:

[math]\displaystyle{ (1,0), (2,1,0), (3,1,0), (4,1,0), (5,2,0), (6,1,0), (7,1,0), (7,3,0), (8,4,3,2,0), (9,4,0)\dots }[/math]

Линейная сложность

Линейная сложность бинарной последовательности – одна из самых важных характеристик работы РСЛОС. Поэтому остановимся на этой теме поподробнее.
Прежде чем дать определение линейной сложности введём некоторые обозначения.
[math]\displaystyle{ S }[/math] - бесконечная последовательность с членами [math]\displaystyle{ S1,S2,S3,\dots }[/math]
[math]\displaystyle{ S_n }[/math] – конечная последовательность длины [math]\displaystyle{ n }[/math], членами которой являются [math]\displaystyle{ S_1,S_2,S_3,\dots,S_{n-1}. }[/math]
Говорят, что РСЛОС генерирует последовательность [math]\displaystyle{ S }[/math], если существует некоторое исходное состояние, при котором выходная последовательность РСЛОС совпадает с [math]\displaystyle{ S }[/math]. Аналогично, говорят, что РСЛОС генерирует конечную последовательность [math]\displaystyle{ S_n }[/math], если существует некоторое начальное состояние, для которого выходная последовательность РСЛОС имеет в качестве первых [math]\displaystyle{ n }[/math] членов члены последовательности [math]\displaystyle{ S_n }[/math].
Наконец дадим определение линейной сложности бесконечной двоичной последовательности.
Определение: Линейной сложностью бесконечной двоичной последовательности [math]\displaystyle{ S }[/math] называется число [math]\displaystyle{ L(S) }[/math], которое определяется следующим образом:

• Если [math]\displaystyle{ S }[/math] – нулевая последовательность [math]\displaystyle{ S=0,0,0,0,\dots, }[/math], то [math]\displaystyle{ L(S)=0. }[/math]
• Если не существует РСЛОС, который генерирует [math]\displaystyle{ S }[/math], то [math]\displaystyle{ L(S) }[/math] равно бесконечности.
• Иначе, [math]\displaystyle{ L(S) }[/math] есть длина самого короткого РСЛОС, который генерирует [math]\displaystyle{ S }[/math].

Определение:
Линейной сложностью конечной двоичной последовательности [math]\displaystyle{ S_n }[/math] называется число [math]\displaystyle{ L(S_n) }[/math], которое равно длине самого короткого РСЛОС, который генерирует последовательность, имеющую в качестве первых [math]\displaystyle{ n }[/math] членов [math]\displaystyle{ S_n }[/math].
Свойства линейной сложности: Пусть [math]\displaystyle{ S }[/math] и [math]\displaystyle{ K }[/math] – двоичные последовательности. Тогда:
1. Для любого [math]\displaystyle{ n\gt 0 }[/math] линейная сложность подпоследовательности [math]\displaystyle{ S_n }[/math] удовлетворяет неравенствам [math]\displaystyle{ 0\leqslant L(S_n) \leqslant n. }[/math]
2. [math]\displaystyle{ L(S_n)=0 }[/math] тогда и только тогда, когда [math]\displaystyle{ S_n }[/math] – нулевая последовательность длины [math]\displaystyle{ n }[/math].
3. [math]\displaystyle{ L(S_n)=n }[/math] тогда и только тогда, когда [math]\displaystyle{ S_n=0,0,0, \dots ,1 }[/math].
4. Если [math]\displaystyle{ S }[/math] – периодическая с периодом [math]\displaystyle{ N }[/math], тогда [math]\displaystyle{ L(S_n)\leqslant N. }[/math]
5. [math]\displaystyle{ L(S \oplus K)\leqslant L(S) + L(K). }[/math]
Эффективным алгоритмом определения линейной сложности конечной двоичной последовательности является алгоритм Берлекемпа-Месси.

Потоковые шифры основанные на РСЛОС. Усложнение

К сожалению, выходная последовательность РСЛОС легко предсказуема. Так, зная 2L знаков выходной последовательности, легко найти исходное заполнение регистра, решив систему линейных уравнений (см. пункт «Потоковые шифры на регистрах сдвига с линейной обратной связью»).

Считается, что для криптографического использования выходная последовательность РСЛОС должна иметь следующие свойства:

• большой период
• высокую линейную сложность
• хорошие статистические свойства

Существует несколько методов проектирования генераторов ключевого потока, которые разрушают линейные свойства РСЛОС и тем самым делают такие системы криптографически более стойкими:
1. использование нелинейной функции, объединяющей выходы нескольких РСЛОС
2. использование нелинейной фильтрующей функции для содержимого каждой ячейки единственного РСЛОС
3. использование выхода одного РСЛОС для управления синхросигналом одного (или нескольких) РСЛОС.

Нелинейная комбинация генераторов

Нелинейная комбинация генераторов

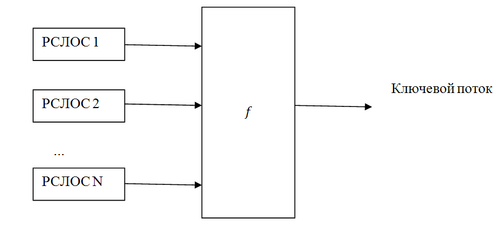
Известно, что каждая Булева функция [math]\displaystyle{ f(x_1,x_2, \dots ,x_n) }[/math] может быть записана как сумма по модулю 2 произведений порядков [math]\displaystyle{ m }[/math] независимых переменных, [math]\displaystyle{ 0 \leqslant m \leqslant n }[/math]. Это выражение называется алгебраической нормальной формой функции [math]\displaystyle{ f }[/math]. Нелинейным порядком функции [math]\displaystyle{ f }[/math] называется максимальный порядок членов в записи её алгебраической нормальной формы.
Например, Булева функция [math]\displaystyle{ f(x_1,x_2,x_3,x_4 )=x_1 \oplus x_2 \oplus x_4 \oplus x_1 x_3 \oplus x_2 x_3 x_4 }[/math] имеет нелинейный порядок 3. Максимально возможный нелинейный порядок Булевой функции равен количеству переменных [math]\displaystyle{ n. }[/math]
Предположим теперь, что у нас [math]\displaystyle{ n }[/math] регистров сдвига с линейной обратной связью, их длины [math]\displaystyle{ L_1, L_2, L_3, \dots , L_n }[/math] попарно различны и больше двух. Все регистры объединены нелинейной функцией [math]\displaystyle{ f(x_1,x_2,\dots,x_n) }[/math], как показано на рисунке. Функция [math]\displaystyle{ f }[/math] представлена в алгебраической нормальной форме. Тогда линейная сложность потока ключей равна [math]\displaystyle{ f(L_1,L_2,\dots,L_n) }[/math].
Если [math]\displaystyle{ L_1, L_2,\dots, L_n }[/math] – попарно взаимно-простые числа, то длина периода ключевого потока равна: [math]\displaystyle{ (2^{L_1}-1)\cdot(2^{L_2}-1) \cdots (2^{L_n }-1) }[/math]. Например, если [math]\displaystyle{ L_i=10 }[/math], то [math]\displaystyle{ (2^{L_1}-1)\approx 10^3 }[/math]. И длина периода ключевого потока равна [math]\displaystyle{ (10^3)^n }[/math].

Генератор Геффа

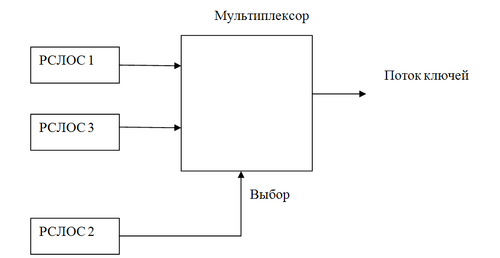
Пример (генератор Геффа):
В этом генераторе используются три РСЛОС, объединённые нелинейным образом. Длины этих регистров [math]\displaystyle{ L_1, L_2, L_3 }[/math] попарно простые числа.
Нелинейную функцию для данного генератора можно записать следующим образом:

[math]\displaystyle{ f(x_1, x_2, x_3 )=x_1 x_2 \oplus (1+x_2 ) x_3=x_1 x_2 \oplus x_2 x_3 \oplus x_3. }[/math]

Длина периода: [math]\displaystyle{ (2^{L_1}-1)\cdot(2^{L_2}-1)\cdot(2^{L_3}-1). }[/math]

Линейная сложность: [math]\displaystyle{ L=L_1\cdot L_2+L_2\cdot L_3+L_3. }[/math]

Генератор Геффа криптографически слаб, потому что информация о состояниях генераторов РСЛОС 1 и РСЛОС 3 содержится в его выходной последовательности. Для того чтобы понять это, обозначим [math]\displaystyle{ x_1 (t),x_2 (t),x_3 (t),z(t) }[/math] [math]\displaystyle{ t }[/math]-е выходные биты РСЛОС 1,2,3 и потока ключей, соответственно. Тогда корреляционная вероятность последовательности [math]\displaystyle{ x_1 (t) }[/math] по отношению к последовательности [math]\displaystyle{ z(t) }[/math]:

[math]\displaystyle{ P(z(t)=x_1 (t) )=P(x_2 (t)=1)+P(x_2 (t)=0)\cdot P(x_3 (t)=x_1 (t) )=1/2+1/2\cdot 1/2=3/4. }[/math]

Аналогично, [math]\displaystyle{ P(z(t)=x_3 (t) )=3/4. }[/math]
По этой причине, несмотря на длинный период и достаточно высокую линейную сложность, генератор Геффа поддаётся корреляционным атакам.

Генератор на нелинейном фильтре

Генераторы на нелинейных фильтрах

Выход каждой ячейки подаётся на вход некоторой нелинейной булевой фильтрующей функции [math]\displaystyle{ f }[/math]. Предположим, что фильтрующая функция порядка [math]\displaystyle{ m }[/math], тогда линейная сложность потока ключей не больше [math]\displaystyle{ L_m=\sum^{m}_{i=1} {L \choose i} }[/math].

Генераторы, основанные на управлении синхросигналом

В нелинейных комбинациях генераторов и генераторах на нелинейных фильтрах перемещение данных во всех РСЛОС контролируется одним синхросигналом.
Основная идея функционирования рассматриваемого типа генераторов — внести нелинейность в работу генераторов потока ключей, основанных на РСЛОС, путём управления синхросигналом одного регистра выходной последовательностью другого.
Есть 2 типа генераторов, основанных на управлении синхросигналом:
1. генератор переменного шага
2. сжимающий генератор.

Генератор переменного шага

Основная идея:
РСЛОС 1 используется для управления передвижением битов двух других РСЛОС 2 и 3.

Генератор переменного шага

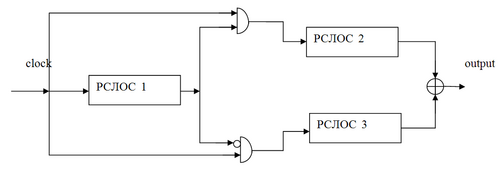
Алгоритм работы:
1. Регистр РСЛОС 1 синхронизован внешним синхросигналом
2. Если на выходе регистра РСЛОС 1 единица, то на регистр РСЛОС 2 подаётся синхросигнал, а РСЛОС 3 повторяет свой предыдущий выходной бит (для начального момента времени предыдущий выходной бит РСЛОС 3 принимается равным 0)
3. Если на выходе регистра РСЛОС 1 ноль, то на регистр РСЛОС 3 подаётся синхросигнал, а РСЛОС 2 повторяет свой предыдущий выходной бит (для начального момента времени предыдущий выходной бит РСЛОС 2 также принимается равным 0)
4. Выходная последовательность битов генератора с переменным шагом является результатом применения операции побитового исключающего ИЛИ к выходным последовательностям регистров РСЛОС 2 и РСЛОС 3.

Увеличение безопасности генераторов с переменным шагом:

• длины регистров РСЛОС 1, РСЛОС 2, РСЛОС 3 должны быть выбраны попарно простыми числами
• длины этих регистров должны быть близкими числами.

Сжимающий генератор

Сжимающий генератор

Контролирующий регистр РСЛОС 1 используется для управления выходом РСЛОС 2. Алгоритм:

1. Регистры РСЛОС 1 и РСЛОС 2 синхронизованы общим синхросигналом;
2. Если выходной бит РСЛОС 1 равен 1, выход генератора формируется выходным битом регистра РСЛОС 2;
3. Если выходной бит РСЛОС 1 равен 0, выходной бит регистра РСЛОС 2 отбрасывается.

Сжимающий генератор прост, масштабируем и имеет хорошие защитные свойства. Его недостаток состоит в том, что скорость генерации ключа не будет постоянной, если не принять некоторых предосторожностей.

Для увеличения безопасности сжимающего генератора:

• длины регистров РСЛОС 1 и РСЛОС 2 должны быть взаимно простыми числами;
• желательно использовать скрытое соединение между регистрами РСЛОС 1 и РСЛОС 2.

Основные отличия поточных шифров от блочных

Большинство существующих шифров с секретным ключом однозначно могут быть отнесены либо к поточным, либо к блочным шифрам. Но теоретическая граница между ними является довольно размытой. Например, используются алгоритмы блочного шифрования в режиме поточного шифрования (пример: для алгоритма DES режимы CFB и OFB).

Рассмотрим основные различия между поточными и блочными шифрами не только в аспектах их безопасности и удобства, но и с точки зрения их изучения в мире:

• важнейшим достоинством поточных шифров перед блочными является высокая скорость шифрования, соизмеримая со скоростью поступления входной информации; поэтому, обеспечивается шифрование практически в реальном масштабе времени вне зависимости от объема и разрядности потока преобразуемых данных.
• в синхронных поточных шифрах (в отличие от блочных) отсутствует эффект размножения ошибок, то есть число искаженных элементов в расшифрованной последовательности равно числу искаженных элементов зашифрованной последовательности, пришедшей из канала связи.
• структура поточного ключа может иметь уязвимые места, которые дают возможность криптоаналитику получить дополнительную информацию о ключе (например, при малом периоде ключа криптоаналитик может использовать найденные части поточного ключа для дешифрования последующего закрытого текста).
• ПШ в отличие от БШ часто могут быть атакованы при помощи линейной алгебры (так как выходы отдельных регистров сдвига с обратной линейной связью могут иметь корреляцию с гаммой). Также для взлома поточных шифров весьма успешно применяется линейный и дифференциальный анализ.

Теперь о положении в мире:

• в большинстве работ по анализу и взлому блочных шифров рассматриваются алгоритмы шифрования, основанные на стандарте DES; для поточных же шифров нет выделенного направления изучения; методы взлома ПШ весьма разнообразны.
• для поточных шифров установлен набор требований, являющихся критериями надёжности (большие периоды выходных последовательностей, постулаты Голомба, нелинейность); для БШ таких чётких критериев нет.
• исследованием и разработкой поточных шифров в основном занимаются европейские криптографические центры, блочных – американские.
• исследование поточных шифров происходит более динамично, чем блочных; в последнее время не было сделано никаких заметных открытий в сфере DES-алгоритмов, в то время как в области поточных шифров случилось множество успехов и неудач (некоторые схемы, казавшиеся стойкими, при дальнейшем исследовании не оправдали надежд изобретателей).

Проектирование поточных шифров

Согласно Райнеру Рюппелю можно выделить четыре основных подхода к проектированию поточных шифров:

• Системно-теоретический подход основан на создании для криптоаналитика сложной, ранее неисследованной проблемы.
• Сложностно-теоретический подход основан на сложной, но известной проблеме (например, факторизация чисел или дискретное логарифмирование).
• Информационно-технический подход основан на попытке утаить открытый текст от криптоаналитика – вне зависимости от того сколько времени потрачено на дешифрование, криптоаналитик не найдёт однозначного решения.
• Рандомизированный подход основан на создании объёмной задачи; криптограф тем самым пытается сделать решение задачи расшифрования физически невозможной. Например, криптограф может зашифровать некоторую статью, а ключом будут указания на то, какие части статьи были использованы при шифровании. Криптоаналитику придётся перебирать все случайные комбинации частей статьи, прежде чем ему повезёт, и он определит ключ.

Теоретические критерии Райнера Рюппеля для проектирования поточных систем:

• длинные периоды выходных последовательностей;
• большая линейная сложность;
• диффузия – рассеивание избыточности в подструктурах, «размазывание» статистики по всему тексту;
• каждый бит потока ключей должен быть сложным преобразованием большинства битов ключа;
• критерий нелинейности для логических функций.

До сих пор не доказано, что эти критерии необходимы или достаточны для безопасности поточной системы шифрования. Стоит также заметить, что, если криптоаналитик обладает неограниченными временем и вычислительной мощностью, то единственным реализуемым потоковым шифром, защищённым от такого противника является одноразовый блокнот.

Криптоанализ. Атаки на поточные шифры

Все методы криптоанализа поточных шифров обычно подразделяют на силовые (атака «грубой силой»), статистические и аналитические.

Силовые атаки

Основная статья: Полный перебор

К этому классу относятся атаки, осуществляющие полный перебор всех возможных вариантов. Сложность полного перебора зависит от количества всех возможных решений задачи (в частности, размера пространства ключей или пространства открытых текстов). Этот класс атак применим ко всем видам систем поточного шифрования. При разработке систем шифрования разработчики стремятся сделать так, чтобы этот вид атак был наиболее эффективным по сравнению с другими существующими методами взлома.

Статистические атаки

Статистические атаки делятся на два подкласса:

• метод криптоанализа статистических свойств шифрующей гаммы: направлен на изучение выходной последовательности криптосистемы; криптоаналитик пытается установить значение следующего бита последовательности с вероятностью выше вероятности случайного выбора с помощью различных статистических тестов.
• метод криптоанализа сложности последовательности: криптоаналитик пытается найти способ генерировать последовательность, аналогичную гамме, но более просто реализуемым способом.

Оба метода используют принцип линейной сложности.

Аналитические атаки

Этот вид атак рассматривается в предположении, что криптоаналитику известны описание генератора, открытый и соответствующий закрытый тексты. Задача криптоаналитика определить использованный ключ (начальное заполнение регистров). Виды аналитических атак, применяемые к синхронным поточным шифрам:

• корреляционные
• компромисс “время-память”
• инверсионная
• “предполагай и определяй”
• на ключевую загрузку и реинициализацию
• XSL-атака

Корреляционные атаки

Являются наиболее распространёнными атаками для взлома поточных шифров.

Известно, что работа по вскрытию криптосистемы может быть значительно сокращена, если нелинейная функция пропускает на выход информацию о внутренних компонентах генератора. Поэтому для восстановления начального заполнения регистров корреляционные атаки исследуют корреляцию выходной последовательности шифросистемы с выходной последовательностью регистров.

Существуют следующие подклассы корреляционных атак:

• Базовые корреляционные атаки
• Атаки, основанные на низко-весовых проверках четности
• Атаки, основанные на использовании сверточных кодов
• Атаки, использующие технику турбо кодов
• Атаки, основанные на восстановлении линейных полиномов
• Быстрые корреляционные атаки.

Базовые корреляционные атаки

Схема базовой корреляционной атаки

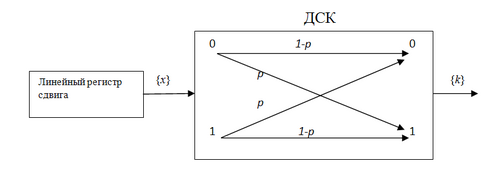
Рассмотрим на примере базовой корреляционной атаки Зигенталера («разделяй и вскрывай»), которая основана на понятии расстояния Хэмминга между двумя двоичными последовательностями одинаковой длины. Применима к комбинирующим генераторам.

Для выявления влияния j-го линейного регистра сдвига (с выходной последовательностью {x^(j)} на гамму шифра {g} моделируется часть генератора как двоичный симметричный канал (ДСК). Алгоритм атаки состоит из двух этапов (иногда называемые фазами):

1. вычисления корреляционной вероятности [math]\displaystyle{ p_j = P(g={x^{(j)}}) }[/math] исходя из комбинирующей функции [math]\displaystyle{ f }[/math] и второго этапа.
2. перебор начальных заполнений регистра. На этом этапе определяется наличие корреляции данного фрагмента гаммы [math]\displaystyle{ g }[/math] с соответствующим фрагментом из [math]\displaystyle{ x_d^{(j)} }[/math], путём вычисления функции кросс-корреляции [math]\displaystyle{ C_{{x^{j},{g}}}(d)=\frac{1}{n}\cdot \sum_{i=1}^n (-1)^{g_i}\cdot(-1)^{x_{i+d}^{(j)}} }[/math] и сравнения этого значения с некоторым числом [math]\displaystyle{ T }[/math].

В случае успеха при сравнении, фаза называется верной и происходит переход к следующему регистру [math]\displaystyle{ j+1 }[/math]. Иначе, фаза называется неверной и переходят к [math]\displaystyle{ d=d+1, d=1,2,\dots,2^{L_j} }[/math]. Выходными значениями этого алгоритма являются состояния [math]\displaystyle{ {x_0^j} }[/math], вносящие информацию в гамму.

Теперь немного о подборе порогового значения [math]\displaystyle{ T }[/math] и необходимого для успешного криптоанализа количество бит гаммы [math]\displaystyle{ n }[/math]: Задаём нужные нам вероятности «ложной тревоги» [math]\displaystyle{ P_f=P(C_{{x^{j},{g}}}(d) \ge T|WrongPhase) }[/math] и пропуска истинного начального заполнения [math]\displaystyle{ P_m=P(C_{{x^{j},{g}}}(d) \lt T|RightPhase) }[/math] .

Например, выбрали [math]\displaystyle{ P_m=0.01, P_f=2^{-L} }[/math], где [math]\displaystyle{ L }[/math] - длина регистра. А затем из этих условий находим [math]\displaystyle{ T }[/math] и [math]\displaystyle{ n }[/math].

Атаки, основанные на низко-весовых проверках четности

Примером этого подкласса атак может служить быстрая корреляционная атака Майера и Штаффельбаха. Применима она как к фильтр-генераторам, так и комбинирующим генераторам и является базовой для всех остальных быстрых корреляционных атак данного типа. Идея атаки основывается на использовании уравнений проверки четности для полинома обратной связи линейного регистра.

Быстрые корреляционные атаки

Под быстрыми корреляционными атаками подразумеваются атаки, вычислительная сложность которых значительно меньше вычислительной сложности силовых атак.
Этот вид атак сводит проблему декодирования в двоичном симметричном канале к проблеме криптоанализа и моделируется как декодирование случайного [math]\displaystyle{ (N,l) }[/math] линейного кода. Аналогично базовым корреляционным атакам, этот подкласс использует понятие расстояния Хэмминга.

Компромисс «время-память»

Цель данной атаки — восстановление исходного состояния регистра сдвига (нахождение ключа), используя известную схему устройства и фрагмент шифрующей последовательности. Сложность атаки зависит от размера шифра и длины перехваченной гаммы.

Состоит из двух этапов:

1. построение большого словаря, в котором записаны всевозможные пары «состояние-выход»;
2. предположение о начальном заполнении регистра сдвига, генерация выхода, просмотр перехваченной выходной последовательности и поиск соответствия со сгенерированным выходом. Если произошло совпадение, то данное предположительное заполнение с большой вероятностью является начальным.

Примерами этого класса атак являются атака Стива Беббиджа и атака Бирюкова-Шамира.

«Предполагай и определяй»

Атака основывается на предположении, что криптоаналитику известны гамма, полином обратной связи, количество сдвигов регистра между выходами схемы и фильтрующая функция. Состоит из трёх этапов:

1. предположение о заполнении некоторых ячеек регистра;
2. определение полного заполнения регистра на основании предположения о знании криптоаналитика;
3. генерация выходной последовательности; если она совпадает с гаммой, то предположение на первом этапе было верно; если не совпадает, то возвращаемся к этапу 1.

Сложность алгоритма зависит от устройства генератора и от количества предположений.

Литература

• Рябко Б. Я., Фионов А. Н. Криптографические методы защиты информации. — Москва. — Изд-во Горяч.Линия-Телеком, 2005. — ISBN 5-93517-265-8.

• Bruce Schneier. Applied Cryptography, Second Edition: Protocols, Algorthms, and Source Code in C (cloth). — John Wiley & Sons, Inc. — Изд-во иностранной литературы, 1996. — ISBN 0471128457.

• A. Menezes, P. van Oorschot, S. Vanstone. Handbook of Applied Cryptography. — CRC Press, Inc. — 1997.

• Лекции Э. М. Габидулина, МФТИ 2009 г.

Ссылки

• Matt J. B. Robshaw. Stream Ciphers Technical Report TR-701 (англ.), версия 2.0, RSA Laboratories, 1995.
• Поточные шифры. Результаты зарубежной открытой криптологии.. Наиболее полная компиляция и перевод современных (вплоть до 1997 г.) зарубежных исследований в области создания и криптоанализа поточных шифров.
• B.C. Анашин, А.Ю. Богданов, И.С. Кижвэтов. eSTREAM: быстрые и стойкие поточные шифры.
• J. A. Reeds and N. J. A. Sloane. Shift-Register Synthesis.
• А.В. Яковлев, А.А. Безбогов, В.В. Родин, В.Н. Шамкин. Криптографическая защита информации.
• Методы и средства защиты компьютерной информации. Учебное пособие.
• Общая схема вероятностной поточной шифрсистемы
• eSTREAM: дитя лохнесского чудовища
• А. А. Меняшев, В. А. Монарев, Б. Я. Рябко, А. Н. Фионов. Статистическая атака.
• S. Doroshenko, A. Fionov, A. Lubkin, V. Monarev, B. Ryabko, Yu. I. Shokin. Experimental Statistical Attacks on Block and Stream Ciphers (недоступная ссылка).
• Ю. В. Стасев, А. В. Потий, Ю. А. Избенко. Исследование методов криптоанализа поточных шифров.