E2 (шифр)

E2
Создатель	NTT
Опубликован	1998
Размер ключа	128 (192, 256) бит
Размер блока	128 бит
Число раундов	12
Тип	Ячейка Фейстеля

E2 (англ. Efficient Encryption — эффективное шифрование) — в криптографии семейство симметричных блочных криптоалгоритмов на основе ячейки Фейстеля. E2 использует блок размером 128 бит и ключи длиной 128, 192, 256 бит. Создан в компании NTT (Nippon Telegraph and Telephone) в 1998 году и был представлен на AES конкурсе. Наследником данного шифра является шифр Camellia, который также является результатом творчества компании NTT (Nippon Telegraph and Telephone).

История

Шифр E2, созданный компанией NTT, был представлен на конкурсе AES вместе с другими четырнадцатью шифрами. E2 прошел тест на криптостойкость успешно. Стойкость шифра E2 не повлияла на его быстродействие. E2 занял одну из лидирующих позиций как в соревновании на скорость шифрования/расшифрования, так и в быстроте формирования ключей. В частности, реализация шифра E2 (компилятор Borland) показала скорость шифрования/расшифрования 26 Мбит/сек. Впрочем, скорость свыше 25 Мбит/сек была показана и пятью другими лидерами. Несмотря на то, что показатели шифра менялись в зависимости от компилятора, платформы и логики, общая тенденция оставалась неизменной. Большинство авторов, писавших о конкурсе AES, утверждают, что E2 наряду с некоторыми другими шифрами успешно прошел первый круг. Однако E2 не попал в финал в пятерку лучших шифров. НИСТ было отмечено, что несмотря на хорошие показатели скорости и отсутствие уязвимостей, требования к энергонезависимой памяти слишком высоки (аналогично пострадал и CAST-256).

Алгоритм шифрования

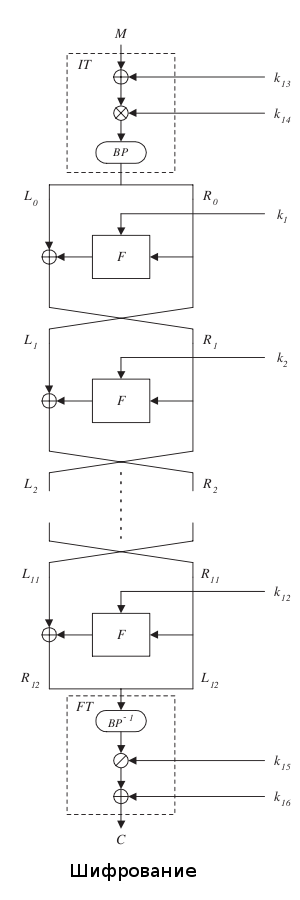
Работу алгоритма шифрования можно разделить на три основные части: IT-функция, или преобразователь начальных данных (англ. initial transformation (IT)), ячейка Фейстеля на базе F-функции, повторяющаяся 12 раз, и FT-функция, или преобразователь конечных данных (англ. finale transformation (FT)). Блок алгоритма, отвечающий за планировку ключей (англ. key sheduling part), до начала шифрования из секретного ключа К создает шестнадцать подключей {k1,..k16}, каждый из которых является 128-разрядным битовым вектором (элементом поля Галуа(2^128)). Первое преобразование открытого текста M производится с помощью IT-функции и двух сгенерированных ключей под номерами 13 и 14([math]\displaystyle{ k_{13} }[/math] и [math]\displaystyle{ k_{14} }[/math])

M‘=IT(M,[math]\displaystyle{ k_{13} }[/math],[math]\displaystyle{ k_{14} }[/math])

M` разбивается на два блока [math]\displaystyle{ L_0 }[/math] и [math]\displaystyle{ R_0 }[/math] равной длины, каждый из элементов [math]\displaystyle{ L_{0} }[/math] и [math]\displaystyle{ R_{0} }[/math] является битовым вектором размерностью 64 бита. Затем выполняются 12 циклов преобразований в ячейке Фейстеля, в которой правый блок на текущей итерации цикла [math]\displaystyle{ R_r }[/math] определяется сложением по модулю два левой части предыдущей итерации цикла [math]\displaystyle{ R_{r-1} }[/math] и результата функции F, аргументами которой являются правая часть предыдущей итерации [math]\displaystyle{ R_{r-1} }[/math] и ключ [math]\displaystyle{ k_r }[/math], а левому блоку на r шаге цикла присваивается значение правого блока на r-1 шаге. Цикл повторяется 12 раз, то есть r изменяется от 1 до 12

[math]\displaystyle{ R_r }[/math] = [math]\displaystyle{ L_{r-1} }[/math][math]\displaystyle{ \oplus F( R_{r-1} , k_r ) }[/math]

[math]\displaystyle{ L_r }[/math] = [math]\displaystyle{ R_{r-1} }[/math].

Финальный этап шифрования — выполнение FT-функции. Результат FT-функции, аргументами которой являются конкатенация правой [math]\displaystyle{ R_{12} }[/math] и левой [math]\displaystyle{ L_{12} }[/math] частей на выходе 12 итерации ячейки Фейстеля и ключи [math]\displaystyle{ k_1 , k_2 }[/math]:

[math]\displaystyle{ C = FT(C }[/math]`[math]\displaystyle{ ,k_{16} , k_{15} ) }[/math]

Алгоритм расшифрования

Расшифрование происходит по схеме, аналогичной шифрованию. Работу алгоритма расшифрования, можно разделить на три основные части: IT-функция (начальное преобразование — англ. initial information (IT)), 12 циклов ячейки Фейстеля с F-функцией и в конце FT-функция (англ. finale transformation (FT)). Блок алгоритма, отвечающий за планировку ключей (англ. key sheduling), из секретного ключа непосредственно перед шифрованием генерирует 16 подключей {[math]\displaystyle{ k_1,k_2,\dots,k_{16} }[/math]}, которые являются битовыми векторами размерностью 128 (элементом поля Галуа GF(2^128)). На первом этапе происходит выполнение IT-функции, аргументами которой являются криптограмма С и два подключа [math]\displaystyle{ {k_{15},k_{16}} }[/math]

[math]\displaystyle{ C }[/math]`[math]\displaystyle{ =IT( C, k_{16}, k_{15}) }[/math]

Результат IT-функции C` разбивается на 2 равные части по 64 бита(половина блока): правую и левую ([math]\displaystyle{ R_{12},L_{12} }[/math]). Далее выполняются 12 циклов ячейки Фейстеля на базе F-Функции ([math]\displaystyle{ r }[/math] меняется от 12 до 1).

[math]\displaystyle{ L_{r-1} = R_{r} \oplus F(L_r,k_r) }[/math]

[math]\displaystyle{ R_{r-1} = L_r }[/math]

По завершении последнего цикла ячейки Фейстеля осуществляется конкатенация половинок блока ([math]\displaystyle{ L_0,R_0 }[/math]). И в конце — финальное преобразование: выполняется FT-функция, аргументами которой являются результат конкатенации [math]\displaystyle{ M }[/math]` и два ключа [math]\displaystyle{ k_{13},k_{14} }[/math]. Результатом выполнения FT-функции является открытый текст [math]\displaystyle{ M }[/math].

[math]\displaystyle{ M = FT(M,k_{13},k_{14}) }[/math]

Генератор ключей (Планировщик ключей)

На основе секретного ключа [math]\displaystyle{ K=(K_1,K_2,K_3,K_4) }[/math] ([math]\displaystyle{ K_i }[/math] {[math]\displaystyle{ i=1;2;3;4 }[/math]} имеет размерность половины блока, то есть 64 бита и является аргументом для функций шифрования и расшифрования) генерируются подключи [math]\displaystyle{ ki }[/math] {i=1;2…16} (битовые вектора размерности 128) с помощью G-функции и S-функции. Процедура генерации ключей остается почти неизменной, если длина секретного ключа равна 128, 192 или 256 бит. Если заданная длина 128 бит, в качестве значений [math]\displaystyle{ K_3,K_4 }[/math] выбираются константы следующим образом: [math]\displaystyle{ K_3=S(S(S(v_{-1}))) }[/math] , [math]\displaystyle{ K_4=S(S(S(S(v_{-1})))) }[/math]. Если длина ключа 192 бита, значение ключа — [math]\displaystyle{ K_4=S(S(S(S(v_{-1})))) }[/math], где S() — S-функция.

Элементарные функции

F-функция

[math]\displaystyle{ F\colon H \times H^{2} \to H }[/math]

[math]\displaystyle{ (X,(K^{(1)},K^{(2)})) \to Y = BRL(S(P S(X \oplus K^{(1)})) \oplus K^{(2)})) }[/math]

BRS(),S(),P() — соответственно BRS-функция, S-функция, P-функция; X,Y — слова двоичного алфавита размерностью 64 бита (половина блока); [math]\displaystyle{ K^{(1)},K^{(2)} }[/math] — ключи размерностью 128 бит каждый. H — пространство размерности 64 бита.

Суть F-функции — преобразование слов бинарного алфавита размерности 64 бита при заданном ключе размерности 128 бит. Результат преобразования — слово бинарного алфавита размерности 64 бита.

IT-Функция (функция начальной обработки)

IT-функция или преобразователь начальных данных:

[math]\displaystyle{ IT\colon H^{2} \times H^{2} \times H^{2} \to H }[/math]

[math]\displaystyle{ (X,A,B) \to Y = BP((X\oplus A) \otimes B) }[/math]

H — пространство слов бинарного алфавита размерности 64 бит; X,A,B — бинарные слова размерности 128 бит; BP() — BP-функция; [math]\displaystyle{ \otimes }[/math] — бинарная операция.

FT-Функция (функция завершающего преобразования)

FT-функция или преобразователь конечных данных:

[math]\displaystyle{ FT\colon H^{2} \times H^{2} \times H^{2} \to H }[/math]

[math]\displaystyle{ (X,A,B) \to Y = BP^{-1}((X de B) \oplus A) }[/math].

H — пространство слов бинарного алфавита размерности 64 бит; X,A,B — бинарные слова размерности 128 бит; [math]\displaystyle{ BP^{-1} }[/math]() — функция, обратная BP-функции; [math]\displaystyle{ de }[/math] — бинарная операция de.

FT-функция — это функция, обратная IT-функции:

[math]\displaystyle{ X=FT(IT(X,A,B),A,B) }[/math].

BRL-Функция

BRL-функция(англ. byte rotate left function), или циклический сдвиг влево, — составляющая часть F-функции:

[math]\displaystyle{ BRL\colon H \to H }[/math]

[math]\displaystyle{ (b1,b2,b3, \dots b8) \to (b2,b3, \dots b8,b1) }[/math]

[math]\displaystyle{ b_i }[/math] {[math]\displaystyle{ i=1 \dots 8 }[/math]} — бинарное слово размерности 8 бит(байт) или, иными словами, элемент поля Галуа [math]\displaystyle{ GF(2)^{8} }[/math].

S-Функция

S-функция — часть F-функции, которая определяется s-box:

[math]\displaystyle{ S\colon H \to H }[/math]

[math]\displaystyle{ (x_1,x_2, \dots x_8) \to (s(x_1),s(x_2), \dots s(x_8)) }[/math].

Структура S-box

S-box, использующийся в S-функции, определяется следующим образом:

[math]\displaystyle{ s:B \to B }[/math]

[math]\displaystyle{ x \to Affine(Power(x,127),97,255) }[/math],

где [math]\displaystyle{ Power(x,e)=x^{e} in GF(2^8) }[/math]

[math]\displaystyle{ Affine(y,a,b)=a*y+b(mod 2^8 Z) }[/math]

Не возбраняется при расчетах пользоваться таблицами c уже вычисленными значениями s(x). То есть [math]\displaystyle{ s(0)=225, s(1)=66, \dots , s(16)=204, \dots , s(255)=42. }[/math]

Таблица вычисленных значений s-box:

225	66	62	129	78	23	158	253	180	63	44	218	49	30	224	65
204	243	130	125	124	18	142	187	228	88	21	213	111	233	76	75
53	123	90	154	144	69	188	248	121	214	27	136	2	171	207	100
9	12	240	1	164	176	246	147	67	99	134	220	17	165	131	139
201	208	25	149	106	161	92	36	110	80	33	128	47	231	83	15
145	34	4	237	166	72	73	103	236	247	192	57	206	242	45	190
93	28	227	135	7	13	122	244	251	50	245	140	219	143	37	150
168	234	205	51	101	84	6	141	137	10	94	217	22	14	113	108
11	255	96	210	46	211	200	85	194	35	183	116	226	155	223	119
43	185	60	98	19	229	148	52	177	39	132	159	215	81	0	97
173	133	115	3	8	64	239	104	254	151	31	222	175	102	232	184
174	189	179	235	198	107	71	169	216	167	114	238	29	126	170	182
117	203	212	48	105	32	127	55	91	157	120	163	241	118	250	5
61	58	68	87	59	202	199	138	24	70	156	191	186	56	86	26
146	77	38	41	162	152	16	153	112	160	197	40	193	109	20	172
249	95	79	196	195	209	252	221	178	89	230	181	54	82	74	42

P-Функция

P-функция — составляющая часть F-функции

[math]\displaystyle{ P\colon H \to H }[/math]

[math]\displaystyle{ \begin{pmatrix} z_{1} \\ \vdots \\ z_{8} \end{pmatrix} \to \begin{pmatrix} z^{|}_{1} \\ \vdots \\ z^{|}_{8} \end{pmatrix} =P \begin{pmatrix} z_{1} \\ \vdots \\ z_{8} \end{pmatrix} }[/math]

P — матрица преобразования описывающая P-функцию

[math]\displaystyle{ P = \begin{pmatrix} 0 & 1 & 1 & 1 & 1 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 1\\ 1 & 1 & 1 & 0 & 1 & 1 & 0 & 1\\ 1 & 1 & 0 & 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 & 1 & 0\\0 & 1 & 1 & 1 & 0 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 & 1 & 0 & 0 & 1 \end{pmatrix} }[/math]

G-Функция

G — функция осуществляет следующее отображение:

[math]\displaystyle{ G \colon H^{4} \times H \to H^4 \times ( \! H^4 \times H ) }[/math]

[math]\displaystyle{ ( \! ( \! X_1 , X_2 , X_3 , X_4 ) \! , U_0) \to ( \! ( \! U_1 , U_2 , U_3 , U_4 \! ), ( \!( \! Y_1 , Y_2 , Y_3 , Y_4 ), V \!) \! ) }[/math] , где

[math]\displaystyle{ Y_i = \! f(X_i) (i = \! 1 , 2 , 3 , 4) }[/math]

[math]\displaystyle{ U_i = \! f(U_{i-1}) \oplus Y_i (i = \! 1 , 2 , 3 , 4) }[/math]

[math]\displaystyle{ V = \! U_4 }[/math]

[math]\displaystyle{ f() }[/math] — f-функция.

f-функция

f-функция необходима для вычисления G-функции. f-функция определяется следующим образом:

[math]\displaystyle{ f \colon H \to H }[/math]

[math]\displaystyle{ X \to P(S(X)) }[/math] , где

P() — P-функция, S() — S-функция.

Бинарный оператор [math]\displaystyle{ \otimes }[/math]

Бинарный оператор [math]\displaystyle{ \otimes }[/math] определяется следующим образом:

[math]\displaystyle{ Y = \! X \otimes B (X , Y , B ) \in H^2 }[/math], где

[math]\displaystyle{ (x_1 , x_2 , x_3 , x_4)=X (x_i \in W, i=1,2,3,4) }[/math]

[math]\displaystyle{ (b_1 , b_2 , b_3 , b_4)=B (b_i \in W, i=1,2,3,4) }[/math]

[math]\displaystyle{ y_i = \! x_i(b_i \lor 1) mod 2^{32} Z (i=1,2,3,4) }[/math]

[math]\displaystyle{ Y = (y_1, y_2, y_3 , y_4) }[/math]

[math]\displaystyle{ \lor 1 }[/math] — логическое побитовое сложение (логическое «или») с 1 в кольце [math]\displaystyle{ 2^{32}Z }[/math].

Бинарный оператор de

Бинарный оператор de определяется следующим образом:

[math]\displaystyle{ Y = \! X de B (X , Y , B \in H^2) }[/math] , где

[math]\displaystyle{ (y_1 , y_2 , y_3 , y_4)=Y (y_i \in W, i=1,2,3,4) }[/math]

[math]\displaystyle{ (b_1 , b_2 , b_3 , b_4)=B (b_i \in W, i=1,2,3,4) }[/math]

[math]\displaystyle{ x_i = \! y_i(b_i \lor 1) mod 2^{32} Z (i=1,2,3,4) }[/math]

[math]\displaystyle{ X = (x_1, x_2, x_3 , x_4) }[/math]

[math]\displaystyle{ \lor 1 }[/math] — логическое побитовое сложение (логическое «или») с 1 в кольце [math]\displaystyle{ 2^{32}Z }[/math].

BP-функция

BP- функция, или функция перестановки байтов (англ. byte permutation), является частью IT-функции и FT — функции. Она определяется следующим образом:

[math]\displaystyle{ BP:W^{4} \to W^{4} }[/math]

[math]\displaystyle{ (x_1 , x_2 , x_3 , x_4) \to (y_1 , y_2 , y_3 , y_4) }[/math] ,где

[math]\displaystyle{ (x_i^{(1)} , x_i^{(2)} , x_i^{(3)} , x_i^{(4)}) = \! x_i (x_i^j \in B {i=1,2,3,4; j=1,2,3,4}) }[/math]

[math]\displaystyle{ y_i = (x_i^{(1)}, x_{i+1}^{(2)}, x_{i+2}^{(3)}, x_{i+3}^{(4)}) (i=1,2,3,4) }[/math]

[math]\displaystyle{ Y = (y_1, y_2, y_3, y_4) }[/math].

Обратное к BP — преобразованию, или BP^{-1}, вычисляется следующим образом:

[math]\displaystyle{ BP^{-1}:W^{4} \to W^{4} }[/math]

[math]\displaystyle{ (y_1 , y_2 , y_3 , y_4) \to (x_1 , x_2 , x_3 , x_4) }[/math] ,где

[math]\displaystyle{ (y_i^{(1)} , y_i^{(2)} , y_i^{(3)} , y_i^{(4)}) = \! y_i (y_i^j \in B {i=1,2,3,4; j=1,2,3,4}) }[/math]

[math]\displaystyle{ x_i = (y_i^{(1)}, y_{i+1}^{(2)}, y_{i+2}^{(3)}, y_{i+3}^{(4)}) (i=1,2,3,4) }[/math]

[math]\displaystyle{ Y = (y_1, y_2, y_3, y_4) }[/math].

Криптоанализ алгоритма

Сотрудниками компании Information Technology R&D Center Mitsubishi Electric Corporation Мицуру Мацуи (Mitsuru Matsui) и Тосио Токита (Toshio Tokita) была обнаружена нестойкость шифра к дифференциальному криптоанализу. Несмотря на это шифр (использующий 12 циклов шифрования) остается стойким с практической точки зрения. Хотя Мицуру Мацуи и Тосио Токита удалось показать, что уровень безопасность шифра E2 с меньшим числом циклов шифрования существенно ниже того, что заявлено разработчиками.

Недостатки шифра

Высокие требования к энергонезависимой памяти.

См. также

• Camellia
• Блочный шифр
• Ячейка Фейстеля
• AES (конкурс)

Ссылки

• Официальный сайт компании Nippon Telegraph and Telephone
• Сайт The National Institute of Standards and Technology