CLEFIA

CLEFIA
Создатель	Тайзо Ширай, Кёдзи Шибутани, Тору Акишита, Шихо Мориаи, Тэцу Ивата
Создан	2007 г.
Опубликован	22 марта 2007 г.
Размер ключа	128, 192, 256 бит
Размер блока	128 бит
Число раундов	18/22/26 (зависит от размера ключа)
Тип	Сеть Фейстеля

CLEFIA (от фр. clef «ключ») — блочный шифр с размером блока 128 битов, длиной ключа 128, 192 или 256 битов и количеством раундов 18, 22, 26 соответственно. Этот криптоалгоритм относится к «легковесным» алгоритмам и использует сеть Фейстеля как основную структурную единицу. CLEFIA был разработан корпорацией Sony и представлен в 2007 году. Авторами являются сотрудники компании Тайдзо Сираи, Кёдзи Сибутани, Тору Акисита, Сихо Мориаи, а также доцент Нагойского университета Тэцу Ивата.

Основное назначение данного шифра — использование в качестве безопасной альтернативы AES в сфере защиты авторских прав и DRM-систем, а также применение в RFID-метках и смарт-картах.

Является одним из самых эффективных криптоалгоритмов при аппаратной реализации: аппаратная реализация CLEFIA может достигать эффективности 400,96 Kbps на эквивалентную логическую ячейку шифратора, что является самым высоким показателем среди алгоритмов, включённых в стандарты ISO на 2008 год.

Алгоритм стал одним из первых шифров, применяющим технологию DSM (англ. Diffusion Switching Mechanism) для увеличения защищённости от линейного и дифференциального криптоанализа.

Схема шифрования данных

Обозначения

[math]\displaystyle{ 0x }[/math]	Префикс для двоичной строки в шестнадцатеричной форме
[math]\displaystyle{ a_{(b)} }[/math]	[math]\displaystyle{ b }[/math] показывает длину [math]\displaystyle{ a }[/math] в битах
[math]\displaystyle{ a \mid b }[/math]	Конкатенация
[math]\displaystyle{ a \leftarrow b }[/math]	Обновление значения [math]\displaystyle{ a }[/math] значением [math]\displaystyle{ b }[/math]
[math]\displaystyle{ a \oplus b }[/math]	Побитовое исключающее ИЛИ
[math]\displaystyle{ a \times b }[/math]	Умножение в [math]\displaystyle{ GF(2^n) }[/math]

Алгоритм состоит из двух составных частей: части обработки ключа и части обработки данных. Число раундов CLEFIA зависит от длины ключа и составляет соответственно 18, 22 или 26 раундов, при этом используется 36, 44 и 52 подключа. Алгоритм использует ключевое забеливание с дополнительным подключами перед обработкой данных и после неё.

Рисунок 1. Один раунд CLEFIA

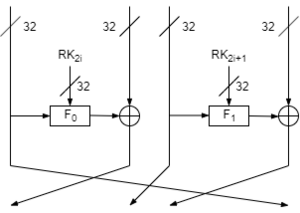
Базовым этапом шифрования данных в CLEFIA является применение обобщённой сети Фейстеля с 4 или 8 ветвями, которая используется как в части обработки данных, так и в части обработки ключа (рисунок 1). В общем случае, если обобщённая сеть Фейстеля имеет d-ветвей и r-раундов, она обозначается как [math]\displaystyle{ GFN_{d,r} }[/math](англ. generalized Feistel network). Далее рассмотрен алгоритм работы сети Фейстеля в случае использования 4-х ветвей и блока данных в 128 бит.

В [math]\displaystyle{ GFN_{4,r} }[/math], кроме 4-x 32-х битных входов ([math]\displaystyle{ X_{i} }[/math]) и 4-x 32-х битных выходов ([math]\displaystyle{ Y_{i} }[/math]), также используются раундовые ключи [math]\displaystyle{ RK_{i} }[/math]. Их количество составляет [math]\displaystyle{ 4r/2=2r }[/math] в связи с тем, что для каждого раунда требуется в два раза меньше ключей, чем ветвей. [math]\displaystyle{ RK_{i} }[/math] генерируются в части обработки ключа.

Каждая ячейка Фейстеля задействует также две различные [math]\displaystyle{ F }[/math]-функции: [math]\displaystyle{ F_0, F_1 }[/math]. [math]\displaystyle{ F }[/math]-функции относятся к SP-типу функций и используют:

• блок подстановок (S-блок, англ. s-box);
• матрицы распространения в поле Галуа (англ. MDS matrix).

F-функции

Две [math]\displaystyle{ F }[/math]-функции [math]\displaystyle{ F_0 }[/math] и [math]\displaystyle{ F_1 }[/math], используемые в [math]\displaystyle{ GFN_{d, r} }[/math], включают в себя нелинейные 8-битные S-блоки [math]\displaystyle{ S_0 }[/math] и [math]\displaystyle{ S_1 }[/math], рассмотренные далее, и матрицы [math]\displaystyle{ M_0 }[/math] и [math]\displaystyle{ M_1 }[/math] размером [math]\displaystyle{ 4 \times 4 }[/math]. В каждой [math]\displaystyle{ F }[/math]-функции эти S-блоки используются в различном порядке, и применяется своя матрица распространения для умножения в поле Галуа. На рисунках показана содержательная часть [math]\displaystyle{ F }[/math]-функций. [math]\displaystyle{ F }[/math]-функции определяются следующим образом:

[math]\displaystyle{ F_0, F_1: \begin{cases} \{0, 1\}^{32} \times \{0, 1\}^{32}\rightarrow \{0, 1\}^{32} \\ (RK_{(32)},x_{(32)}) \rightarrow y_{(32)} \end{cases} }[/math]

Функция [math]\displaystyle{ F_0 }[/math]
 Шаг 1. [math]\displaystyle{ T = RK \oplus x }[/math]
 Шаг 2. [math]\displaystyle{ T_0=S_0(T_0),\ T_1=S_1(T_1),\ T_2=S_0(T_2),\ T_3=S_1(T_3),\ \mbox{where}\ T=T_0|T_1|T_2|T_3,\ T_i \in \{0,1\}^8 }[/math]
 Шаг 3. [math]\displaystyle{ \begin{pmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \end{pmatrix}=M_0\begin{pmatrix} T_0 \\ T_1 \\ T_2 \\ T_3 \end{pmatrix},\ \mbox{where}\ y=y_0|y_1|y_2|y_3,\ y_i \in \{0,1\}^8 }[/math]

Функция [math]\displaystyle{ F_1 }[/math]
 Шаг 1. [math]\displaystyle{ T = RK \oplus x }[/math]
 Шаг 2. [math]\displaystyle{ T_0=S_1(T_0),\ T_1=S_0(T_1),\ T_2=S_1(T_2),\ T_3=S_0(T_3),\ \mbox{where}\ T=T_0|T_1|T_2|T_3,\ T_i \in \{0,1\}^8 }[/math]
 Шаг 3. [math]\displaystyle{ \begin{pmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \end{pmatrix}=M_1\begin{pmatrix} T_0 \\ T_1 \\ T_2 \\ T_3 \end{pmatrix},\ \mbox{where}\ y=y_0|y_1|y_2|y_3,\ y_i \in \{0,1\}^8 }[/math]

S-блоки

В CLEFIA используется два разных типа S-блоков, размером по 8 бит каждый. Они сгенерированы так, чтобы минимализировать занимаемую ими площадь при аппаратной реализации. Первый ([math]\displaystyle{ S_0 }[/math]) состоит из 4-битных случайных S-блоков. Во втором ([math]\displaystyle{ S_1 }[/math]) используется обратная функции над полем [math]\displaystyle{ GF(2^8) }[/math]. В таблицах ниже представлены выходные значения в шестнадцатеричной системе счисления для S-блоков. Старшие 4-бита для 8-битного ввода S-блока обозначают строку, а младшие 4-бита обозначают столбец. Например, если введено значение [math]\displaystyle{ 0x32 }[/math], то блок [math]\displaystyle{ S_0 }[/math] выводит [math]\displaystyle{ 0x2e }[/math].

Первый S-блок

[math]\displaystyle{ S_0 }[/math] создан с помощью применения четырёх 4-битных S-блоков [math]\displaystyle{ SS_0, SS_1, SS_2, SS_3 }[/math] следующим образом:

[math]\displaystyle{ S_0: \begin{cases} \{0, 1\}^8 \rightarrow \{0, 1\}^8 \\ x_{(8)} \rightarrow y_{(8)} \end{cases} }[/math]

Алгоритм получения выходных данных при использования блока [math]\displaystyle{ S_0 }[/math]
 Шаг 1. [math]\displaystyle{ t_0 = SS_0(x_0),\ t1 = SS_1(x_1),\ \mbox{where } x = x_0|x_1,\ x_i \in \{0, 1\}^4 }[/math]
 Шаг 2. [math]\displaystyle{ u_0 = t_0 \oplus 0x2 \times t_1,\ u_1 = 0x2 \times t_0 \oplus t_1 }[/math]
 Шаг 3. [math]\displaystyle{ y_0 = SS_2(u_0),\ y_1 = SS_3(u_1),\ \mbox{where } y = y_0|y_1,\ y_i \in \{0, 1\}^4 }[/math]

Умножение в [math]\displaystyle{ 0x2 \times t_i }[/math] выполняется в [math]\displaystyle{ GF(2^4) }[/math] над многочленами, которое определяется неприводимым полиномом [math]\displaystyle{ z^4 + z + 1 }[/math]. В таблице можно найти соответствующий полученный S-box [math]\displaystyle{ S_0 }[/math].

Таблица [math]\displaystyle{ S_0 }[/math] .0 .1 .2 .3 .4 .5 .6 .7 .8 .9 .a .b .c .d .e .f 0. 57 49 d1 c6 2f 33 74 fb 95 6d 82 ea 0e b0 a8 1c 1. 28 d0 4b 92 5c ee 85 b1 c4 0a 76 3d 63 f9 17 af 2. bf a1 19 65 f7 7a 32 20 06 ce e4 83 9d 5b 4c d8 3. 42 5d 2e e8 d4 9b 0f 13 3c 89 67 c0 71 aa b6 f5 4. a4 be fd 8c 12 00 97 da 78 e1 cf 6b 39 43 55 26 5. 30 98 cc dd eb 54 b3 8f 4e 16 fa 22 a5 77 09 61 6. d6 2a 53 37 45 c1 6c ae ef 70 08 99 8b 1d f2 b4 7. e9 c7 9f 4a 31 25 fe 7c d3 a2 bd 56 14 88 60 0b 8. cd e2 34 50 9e dc 11 05 2b b7 a9 48 ff 66 8a 73 9. 03 75 86 f1 6a a7 40 c2 b9 2c db 1f 58 94 3e ed a. fc 1b a0 04 b8 8d e6 59 62 93 35 7e ca 21 df 47 b. 15 f3 ba 7f a6 69 c8 4d 87 3b 9c 01 e0 de 24 52 c. 7b 0c 68 1e 80 b2 5a e7 ad d5 23 f4 46 3f 91 c9 d. 6e 84 72 bb 0d 18 d9 96 f0 5f 41 ac 27 c5 e3 3a e. 81 6f 07 a3 79 f6 2d 38 1a 44 5e b5 d2 ec cb 90 f. 9a 36 e5 29 c3 4f ab 64 51 f8 10 d7 bc 02 7d 8e

Таблица [math]\displaystyle{ SS_i (0 \le i \lt 4) }[/math] [math]\displaystyle{ x }[/math] 0 1 2 3 4 5 6 7 8 9 a b c d e f [math]\displaystyle{ SS_0(x) }[/math] e 6 c a 8 7 2 f b 1 4 0 5 9 d 3 [math]\displaystyle{ SS_1(x) }[/math] 6 4 0 d 2 b a 3 9 c e f 8 7 5 1 [math]\displaystyle{ SS_2(x) }[/math] b 8 5 e a 6 4 c f 7 2 3 1 0 d 9 [math]\displaystyle{ SS_3(x) }[/math] a 2 6 d 3 4 5 e 0 7 8 9 b f c 1

Второй S-блок

Блок [math]\displaystyle{ S_1 }[/math] определяется как:

[math]\displaystyle{ S_1: \begin{cases} \{0, 1\}^8 \rightarrow \{0, 1\}^8 \\ x_{(8)} \rightarrow y_{(8)} \end{cases} }[/math] [math]\displaystyle{ y= \begin{cases} g(f(x)^{-1}), & \mbox{if} \quad f(x) \ne 0 \\ g(0), & \mbox{if} \quad f(x) = 0 \end{cases} }[/math]

При этом обратная функция находится в поле [math]\displaystyle{ GF(2^8) }[/math], которое задано неприводимым полиномом [math]\displaystyle{ z^8+z^4+z^3+z^2+1 }[/math]. [math]\displaystyle{ f(\cdot) \mbox{ и } g(\cdot) }[/math] — аффинные преобразования над [math]\displaystyle{ GF(2) }[/math], определённые следующим образом:

[math]\displaystyle{ f: \begin{cases} \{0, 1\}^8 \rightarrow \{0, 1\}^8 \\ x_{(8)} \rightarrow y_{(8)} \end{cases} }[/math] [math]\displaystyle{ \begin{pmatrix} y_0 \\ y_1 \\y_2 \\y_3 \\y_4 \\y_5 \\y_6 \\y_7 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_0 \\ x_1 \\x_2 \\x_3 \\x_4 \\x_5 \\x_6 \\x_7 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ 0 \end{pmatrix} }[/math]

[math]\displaystyle{ g: \begin{cases} \{0, 1\}^8 \rightarrow \{0, 1\}^8 \\ x_{(8)} \rightarrow y_{(8)} \end{cases} }[/math] [math]\displaystyle{ \begin{pmatrix} y_0 \\ y_1 \\y_2 \\y_3 \\y_4 \\y_5 \\y_6 \\y_7 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \end{pmatrix} \begin{pmatrix} x_0 \\ x_1 \\x_2 \\x_3 \\x_4 \\x_5 \\x_6 \\x_7 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \end{pmatrix} }[/math]

Здесь используется, что [math]\displaystyle{ x = x_0|x_1|x_2|x_3|x_4|x_5|x_6|x_7 }[/math] и [math]\displaystyle{ y = y_0|y_1|y_2|y_3|y_4|y_5|y_6|y_7,\ x_i,\ y_i \in \{0, 1\} }[/math]. Таким образом получается блок [math]\displaystyle{ S_1 }[/math].

Таблица [math]\displaystyle{ S_1 }[/math]

	.0	.1	.2	.3	.4	.5	.6	.7	.8	.9	.a	.b	.c	.d	.e	.f
0.	6c	da	c3	e9	4e	9d	0a	3d	b8	36	b4	38	13	34	0c	d9
1.	bf	74	94	8f	b7	9c	e5	dc	9e	07	49	4f	98	2c	b0	93
2.	12	eb	cd	b3	92	e7	41	60	e3	21	27	3b	e6	19	d2	0e
3.	91	11	c7	3f	2a	8e	a1	bc	2b	c8	c5	0f	5b	f3	87	8b
4.	fb	f5	de	20	c6	a7	84	ce	d8	65	51	c9	a4	ef	43	53
5.	25	5d	9b	31	e8	3e	0d	d7	80	ff	69	8a	ba	0b	73	5c
6.	6e	54	15	62	f6	35	30	52	a3	16	d3	28	32	fa	aa	5e
7.	cf	ea	ed	78	33	58	09	7b	63	c0	c1	46	1e	df	a9	99
8.	55	04	c4	86	39	77	82	ec	40	18	90	97	59	dd	83	1f
9.	9a	37	06	24	64	7c	a5	56	48	08	85	d0	61	26	ca	6f
a.	7e	6a	b6	71	a0	70	05	d1	45	8c	23	1c	f0	ee	89	ad
b.	7a	4b	c2	2f	db	5a	4d	76	67	17	2d	f4	cb	b1	4a	a8
c.	b5	22	47	3a	d5	10	4c	72	cc	00	f9	e0	fd	e2	fe	ae
d.	f8	5f	ab	f1	1b	42	81	d6	be	44	29	a6	57	b9	af	f2
e.	d4	75	66	bb	68	9f	50	02	01	3c	7f	8d	1a	88	bd	ac
f.	f7	e4	79	96	a2	fc	6d	b2	6b	03	e1	2e	7d	14	95	1d

Матрицы распространения

Матрицы распространения заданы следующим образом:

[math]\displaystyle{ M_0: \begin{pmatrix} 0x01 & 0x02 & 0x04 & 0x06 \\ 0x02 & 0x01 & 0x06 & 0x04 \\ 0x04 & 0x06 & 0x01 & 0x02 \\ 0x06 & 0x04 & 0x02 & 0x01 \end{pmatrix} }[/math]

[math]\displaystyle{ M_1: \begin{pmatrix} 0x01 & 0x08 & 0x02 & 0x0a \\ 0x08 & 0x01 & 0x0a & 0x02 \\ 0x02 & 0x0a & 0x01 & 0x08 \\ 0x0a & 0x02 & 0x08 & 0x01 \end{pmatrix} }[/math]

Умножения матрицы и векторов выполняются в поле [math]\displaystyle{ GF(2^8) }[/math], определённое неприводимым полиномом [math]\displaystyle{ z^8+z^4+z^3+z^2+1 }[/math].

Общая структура шифрования

Таким образом, на основе обобщённой сети Фейстеля (4 входа для блока данных; 2r входа для раундовых ключей; 4 выхода для шифротекста):

[math]\displaystyle{ GFN_{4,r}: \begin{cases} \{ \{0,1\}^{32} \}^{2r} \times \{ \{0,1\}^{32} \}^{2r} \rightarrow \{ \{0,1\}^{32} \}^{4} \\ (RK_{0(32)},...,RK_{2r-1(32)},X_{0(32)},X_{1(32)},X_{2(32)},X_{3(32)}) \rightarrow (Y_{0(32)},Y_{1(32)},Y_{2(32)},Y_{3(32)}) \end{cases} }[/math]

Алгоритм шифрования и расшифрования данных:

Шифрование ([math]\displaystyle{ GFN_{4,r} }[/math])
 Шаг 1. [math]\displaystyle{ T_0=X_0,\ T_1=X_1,\ T_2=X_2,\ T_3=X_3 }[/math]
 Шаг 2. [math]\displaystyle{ \mbox{for } i=0 \mbox{ to } r-1  \mbox{ do:} }[/math]
   Шаг 2.1. [math]\displaystyle{ T_1=T_1\oplus F_0(RK_{2i},T_0), }[/math]
   Шаг 2.2. [math]\displaystyle{ T_3=T_3\oplus F_1(RK_{2i+1},T_2), }[/math]
 Шаг 3. [math]\displaystyle{ Y_0=T_3,\ Y_1=T_0,\ Y_2=T_1,\ Y_3=T_2 }[/math]

Расшифрование ([math]\displaystyle{ GFN_{4,r}^{-1} }[/math])
 Шаг 1. [math]\displaystyle{ T_0=X_0,\ T_1=X_1,\ T_2=X_2,\ T_3=X_3 }[/math]
 Шаг 2. [math]\displaystyle{ \mbox{for } i=0 \mbox{ to } r-1  \mbox{ do:} }[/math]
   Шаг 2.1. [math]\displaystyle{ T_1=T_1\oplus F_0(RK_{2(r-i)-2},T_0), }[/math]
   Шаг 2.2. [math]\displaystyle{ T_3=T_3\oplus F_1(RK_{2(r-i)-1},T_2), }[/math]
 Шаг 3. [math]\displaystyle{ Y_0=T_1,\ Y_1=T_2,\ Y_2=T_3,\ Y_3=T_0 }[/math]

Число раундов [math]\displaystyle{ r }[/math] составляет 18, 22 и 26 для 128-битных, 192-битных и 256-битных ключей соответственно. Общее количество [math]\displaystyle{ RK_i }[/math] зависит от длины ключа, поэтому часть обработки данных требует 36, 44 и 52 раундовых ключей для 128-битных, 192-битных и 256-битных ключей соответственно.

Результат от [math]\displaystyle{ GFN_{4,r} }[/math] также подвергается ключевому забеливанию.

Использование ключевого забеливания

Рисунок 4. Схема шифрования данных

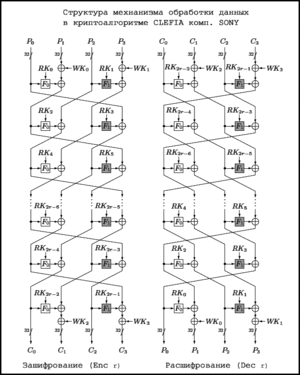
В часть обработки данных CLEFIA, состоящую из [math]\displaystyle{ ENC_r }[/math] для шифрования и [math]\displaystyle{ DEC_r }[/math] для расшифрования, входят процедуры исключающее «или» между текстом и отбеливающими ключами в начале и в конце алгоритма.

Таким образом, пусть [math]\displaystyle{ P, C \in \{0, 1\}^{128} }[/math] — открытый текст и зашифрованный текст, и пусть [math]\displaystyle{ P_i, C_i \in \{0, 1\}^{32}\ (0 \le i\lt 4) }[/math] — части открытого текста и зашифрованного текста, где [math]\displaystyle{ P = P_0 | P_1 | P_2 | P_3 }[/math] и [math]\displaystyle{ C = C_0 | C_1 | C_2 | C_3 }[/math], и пусть [math]\displaystyle{ WK_0, WK_1, WK_2, WK_3 \in \{0, 1\}^{32} }[/math] — отбеливающие ключи, а [math]\displaystyle{ RK_i \in \{0, 1\}^{32}\ (0 \le i \lt 2r) }[/math] — раундовые ключи, предоставляемые частью обработки ключа. Тогда алгоритм шифрования с использованием ключевого забеливания:

Функция шифрования [math]\displaystyle{ ENC_r }[/math]
 Шаг 1. [math]\displaystyle{ T_0=P_0,\ T_1=P_1 \oplus WK_0,\ T_2=P_2,\ T_3=P_3 \oplus WK_1 }[/math]
 Шаг 2. [math]\displaystyle{ T_0,T_1,T_2,T_3 \leftarrow GFN_{4, r} (RK_0, ..., RK_{2r - 1}, T_0, T_1, T_2, T_3) }[/math]
 Шаг 3. [math]\displaystyle{ C_0=T_0,\ C_1=T_1 \oplus WK_2,\ C_2=T_2,\ C_3=T_3 \oplus WK_3 }[/math]

Функция расшифрования [math]\displaystyle{ DEC_r }[/math]
 Шаг 1. [math]\displaystyle{ T_0=C_0,\ T_1=C_1 \oplus WK_2,\ T_2=C_2,\ T_3=C_3 \oplus WK_3 }[/math]
 Шаг 2. [math]\displaystyle{ T_0,T_1,T_2,T_3 \leftarrow GFN_{4, r}^{-1} (RK_0, ..., RK_{2r - 1}, T_0, T_1, T_2, T_3) }[/math]
 Шаг 3. [math]\displaystyle{ P_0=T_0,\ P_1=T_1 \oplus WK_0,\ P_2=T_2,\ P_3=T_3 \oplus WK_1 }[/math]

Алгоритм обработки ключа

Часть обработки ключей в шифре CLEFIA поддерживает 128, 192 и 256-битные ключи и в результате выдаёт отбеливающие ключи [math]\displaystyle{ WK_i (0 \le i \lt 4) }[/math] и раундовые ключи [math]\displaystyle{ RK_j (0 \le j \lt 2r) }[/math] для части обработки данных. Пусть [math]\displaystyle{ K }[/math] будет ключом, а [math]\displaystyle{ L }[/math] — промежуточным ключом (получается с помощью сокращённой части обработки данных), тогда часть обработки ключа состоит в трёх этапах:

1. Генерация [math]\displaystyle{ L }[/math] из [math]\displaystyle{ K }[/math].
2. Генерация [math]\displaystyle{ WK_i }[/math] из [math]\displaystyle{ K }[/math].
3. Генерация [math]\displaystyle{ RK_j }[/math] из [math]\displaystyle{ K }[/math] и [math]\displaystyle{ L }[/math].

Чтобы сгенерировать [math]\displaystyle{ L }[/math] из [math]\displaystyle{ K }[/math], часть обработки ключа для 128-битного ключа использует 128-битную [math]\displaystyle{ GFN_{4,12} }[/math](4 входа по 32 бита), в то время как для 192/256-битных ключей используется 256-битная [math]\displaystyle{ GFN_{8,10} }[/math](8 входов по 32 бита). Далее приведёно описание алгоритма в случае 128-битного ключа.

Функция перестановки бит

Данный алгоритм использует функцию перестановки бит DoubleSwap (обозначение: [math]\displaystyle{ \Sigma }[/math]):

[math]\displaystyle{ \Sigma: \begin{cases} \{0,1\}^{128} \rightarrow \{0,1\}^{128} \\ X_{(128)} \rightarrow Y_{(128)} \end{cases} }[/math]
[math]\displaystyle{ Y=\Sigma (X)=X[7-63]|X[121-127]|X[0-6]|X[64-120] }[/math]

Причём [math]\displaystyle{ X[a-b] }[/math] обозначает битовую строку, вырезанную с [math]\displaystyle{ a }[/math]-го бита по [math]\displaystyle{ b }[/math]-й бит из [math]\displaystyle{ X }[/math].

Генерация констант

Схема [math]\displaystyle{ GFN_{d,r} }[/math] требует на вход раундовые ключи в количестве [math]\displaystyle{ r \cdot \frac{d}{2}=2r }[/math] (если [math]\displaystyle{ d=4 }[/math]), и, когда эта схема применяется в части обработки ключа, шифр CLEFIA применяет заранее сгенерированные константы как раундовые ключи. Также дополнительные константы необходимы при втором этапе, при генерации [math]\displaystyle{ WK_i }[/math] и [math]\displaystyle{ RK_j }[/math], и их количество равно [math]\displaystyle{ r \cdot \frac{d}{2} }[/math] (но в данном случае константы [math]\displaystyle{ d }[/math] и [math]\displaystyle{ r }[/math] из части обработки данных).

Эти 32-х битные константы обозначаются как [math]\displaystyle{ CON_i^{(k)} }[/math], где [math]\displaystyle{ i }[/math] — номер константы, [math]\displaystyle{ k }[/math] — используемое количество бит для ключа(может быть 128, 196, 256). Тогда количество констант будет 60, 84, 92 для 128, 192, 256 битовых ключей соответственно.

Пусть [math]\displaystyle{ P_{(16)}=0xb7e1(=(e-2) \cdot 2^{16}) }[/math] и [math]\displaystyle{ Q_{(16)}=0x243f(=(\pi-3) \cdot 2^{16}) }[/math]. Тогда алгоритм для генерации (в таблице количество итераций [math]\displaystyle{ l^{(k)} }[/math] и начальные значения [math]\displaystyle{ IV^{(k)} }[/math]):

Шаг 1. [math]\displaystyle{ T_0 = IV^{(k)} }[/math]
Шаг 2. [math]\displaystyle{ \mbox{for } i = 0 \mbox{ to } l^{(k)}-1 \mbox{ do:} }[/math]
  Шаг 2.1. [math]\displaystyle{ CON_{2i}^{(k)} = (T_i \oplus P_{(16)}) | (\overline{T_i} \lll 1) }[/math]
  Шаг 2.2. [math]\displaystyle{ CON_{2i+1}^{(k)} = (\overline{T_i} \oplus Q_{(16)}) | (T_i \lll 8) }[/math]
  Шаг 2.3. [math]\displaystyle{ T_{i+1} = T_i \times 0x0002^{-1} }[/math]

Где [math]\displaystyle{ \overline{a} }[/math] — логическое отрицание, [math]\displaystyle{ a \lll b }[/math] — циклический левый сдвиг на [math]\displaystyle{ b }[/math]-бит; а умножение происходит в поле [math]\displaystyle{ GF(2^{16}) }[/math] и определённо неприводимым многочленом [math]\displaystyle{ z^{16}+z^{15}+z^{13}+z^{11}+z^5+z^4+1(=0x1a831) }[/math].

Обработка ключа в случае 128-битного ключа

128-разрядный промежуточный ключ [math]\displaystyle{ L }[/math] генерируется путём применения [math]\displaystyle{ GFN_{4,12} }[/math], который принимает на вход двадцать четыре 32-разрядные константы [math]\displaystyle{ CON_i^{(128)} (0 \le i \lt 24) }[/math] в качестве раундовых ключей и [math]\displaystyle{ K = K_0 | K_1 | K_2 | K_3 }[/math] в качестве данных для шифрования. Затем [math]\displaystyle{ K }[/math] и [math]\displaystyle{ L }[/math] используются для генерации [math]\displaystyle{ WK_i (0 \le i \lt 4) }[/math] и [math]\displaystyle{ RK_j (0 \le j \lt 36) }[/math] в следующих шагах:

Генерация [math]\displaystyle{ L }[/math] из [math]\displaystyle{ K }[/math]:
 Шаг 1. [math]\displaystyle{ L = GFN_{4,12}(CON^{(128)}_0, ... , CON^{(128)}_{23} , K_0, K_1,K_2 , K_3) }[/math]

Генерация [math]\displaystyle{ WK_i }[/math] из [math]\displaystyle{ K }[/math]:
 Шаг 2. [math]\displaystyle{ WK_0|WK_1|WK_2|WK_3 \leftarrow K }[/math]

Генерация [math]\displaystyle{ RK_j }[/math] из [math]\displaystyle{ K }[/math] и [math]\displaystyle{ L }[/math]:
 Шаг 3. [math]\displaystyle{ \mbox{for } i = 0 \mbox{ to } 8 \mbox{ do:} }[/math]
   Шаг 3.1. [math]\displaystyle{ T = L \oplus (CON^{(128)}_{24+4i}| CON^{(128)}_{24+4i+1} | CON^{(128)}_{24+4i+2} | CON^{(128)}_{24+4i+3}) }[/math]
   Шаг 3.2. [math]\displaystyle{ L = \Sigma(L) }[/math]
   Шаг 3.3. [math]\displaystyle{ \mbox{if }\ i\ \mbox{mod}\ 2 == 1:\ T = T \oplus K }[/math]
   Шаг 3.4. [math]\displaystyle{ RK_{4i}|RK_{4i+1}|RK_{4i+2}|RK_{4i+3} \leftarrow T }[/math]

Особенности шифра

CLEFIA может быть эффективно реализована как в аппаратном, так и в программном обеспечении. В таблице показаны основные преимущества технологий, использованных в этом шифре.

Аспекты проектирования для эффективной реализации

[math]\displaystyle{ GFN }[/math]	[math]\displaystyle{ F }[/math]-функции небольшого размера (32-битный вход/выход) Нет необходимости в обратимости [math]\displaystyle{ F }[/math]-функций
SP-тип [math]\displaystyle{ F }[/math]-функций	Возможность быстрой табличной реализации в программном обеспечении
DSM	Сокращение количества раундов
S-блоки	Очень маленькая занимаемая площадь [math]\displaystyle{ S_0 }[/math] и [math]\displaystyle{ S_1 }[/math] в аппаратном обеспечении
Матрицы	Использование элементов только с малым весом Хэмминга
Часть обработки ключа	Совместное использование структуры с частью обработки данных Требуется только 128-битный регистр для 128-битного ключа Небольшая площадь функции DoubleSwap

Преимуществами и особенностями в алгоритма CLEFIA являются:

• Обобщённую сеть Фейстеля [math]\displaystyle{ GFN }[/math];
• DSM (англ. Diffusion Switching Mechanism);
• Два S-бокса.

Особенности реализации GFN

Схема 1. Сравнение обобщённой структуры Фейстеля второго типа и обычной структуры Фейстеля

CLEFIA использует обобщённую структуру Фейстеля с 4 ветвями, которая рассматривается как расширение традиционной структуры Фейстеля с 2 ветвями. Существует много типов обобщённых структур Фейстеля. В алгоритме CLEFIA используется второй тип этой структуры (схема 1). Структура второго типа имеет две F-функции в одном раунде для четырёх линий данных.

Структура типа 2 имеет следующие особенности:

• [math]\displaystyle{ F }[/math]-функции меньше, чем у традиционной структуры Фейстеля;
• множественные [math]\displaystyle{ F }[/math]-функции могут обрабатываться одновременно;
• как правило, требует больше раундов, чем традиционная структура Фейстеля.

Первая особенность является большим преимуществом для программных и аппаратных реализаций; а вторая особенность подходит для эффективной реализации, особенно в аппаратном обеспечение. Но при этом, заметно увеличивается количество раундов из-за третьей особенности. Однако преимущества структуры второго типа превосходят недостатки для данной конструкции блочного шифр, так как используется новая методика программирования, использующая DSM и два типа S-боксов, что позволяет эффективно сократить количество раундов.

Использование Diffusion Switching Mechanism

Схема 2. Применение DSM в обобщённой структуре Фейстеля

CLEFIA использует две разные матрицы распространения для повышения устойчивости к дифференциальным атакам и линейным атакам с использованием механизма DSM (схема 2). Эта методика проектирования была первоначально разработана для традиционных сетей Фейстеля. Эта техника была перенесена на [math]\displaystyle{ GFN_{d,r} }[/math], что является одним из уникальных свойств этого шифра. Также, благодаря DSM можно увеличить гарантированное количество активных S-блоков при том же количество раундов.

Следующая таблица показывает гарантированное количество активных S-блоков в шифре CLEFIA. Данные получены при помощи компьютерного моделирования с использованием алгоритма поиска исчерпывающего типа. Столбцы «D» и «L» в таблице показывают гарантированное количество активных S-блоков при дифференциальном и линейном криптоанализе соответственно. Из этой таблицы можно видеть, что влияние DSM проявляется уже при [math]\displaystyle{ r \ge 3 }[/math], и гарантированное количество S-боксов увеличиваются примерно на 20 % — 40 %, в отличие от структуры без DSM. Следовательно, количество раундов может быть уменьшено, что означает, что производительность улучшается.

Гарантированное число активных S боксов
Количество раундов 1 — 13 Раунды Дифф. и Лин. (без DSM) Дифф. (с DSM) Лин. (с DSM) 1 0 0 0 2 1 1 1 3 2 2 5 4 6 6 6 5 8 8 10 6 12 12 15 7 12 14 16 8 13 18 18 9 14 20 20 10 18 22 23 11 20 24 26 12 24 28 30 13 24 30 32
Количество раундов 14 — 26 Раунды Дифф. и Лин. (без DSM) Дифф. (с DSM) Лин. (с DSM) 14 25 34 34 15 26 36 36 16 30 38 39 17 32 40 42 18 36 44 46 19 36 44 46 20 37 50 50 21 38 52 52 22 42 55 55 23 44 56 58 24 48 59 62 25 48 62 64 26 49 65 66

В таблице красным выделена строка, указывающая на минимальное требуемое количество раундов, чтобы шифр был устойчив к криптоанализу методом полного перебора(см. также). Синим цветом выделены строки, количество раундов которых используется в алгоритме CLEFIA с 128/192/256-битовыми ключами соответственно.

Особенности двух S-боксов

CLEFIA использует два разных типа 8-битных S-блоков: один основан на четырёх 4-битных случайных S-блоках; а другой основан на обратной функции в [math]\displaystyle{ GF(2^8) }[/math], которая имеет максимально возможную трудоёмкость атаки для дифференциального криптоанализа [math]\displaystyle{ DP_{max} }[/math] и линейного криптоанализа [math]\displaystyle{ LP_{max} }[/math]. Оба S-блока выбраны для эффективной реализации, особенно в аппаратном обеспечении.

Для параметров безопасности [math]\displaystyle{ DP_{max} }[/math] [math]\displaystyle{ S_0 }[/math] составляет [math]\displaystyle{ 2^{-4.67} }[/math], а его [math]\displaystyle{ LP_{max} }[/math] составляет [math]\displaystyle{ 2^{-4.38} }[/math]. Для [math]\displaystyle{ S_1 }[/math] [math]\displaystyle{ DP_{max} }[/math] и [math]\displaystyle{ LP_{max} }[/math] оба равны [math]\displaystyle{ 2^{-6.00} }[/math].

Криптостойкость

Дифференциальный криптоанализ

По таблице количества активных S боксов с DSM(в пункте Использование Diffusion Switching Mechanism) минимальное число раундов равно 12. Таким образом, используя 28 активных S-блоков для 12-раундового CLEFIA и [math]\displaystyle{ DP^{S_0}_{max} = 2^{-4.67} }[/math](см. также), определяем, что вероятность характеристики [math]\displaystyle{ DCP^{12r}_{max} \le 2^{28 \cdot (-4.67)} = 2^{-130.76} }[/math]. Это означает, что трудоёмкость атаки выше [math]\displaystyle{ 2^{128} }[/math] и для атакующего нет полезной дифференциальной характеристики в 12 раундов. Кроме того, поскольку [math]\displaystyle{ S_1 }[/math] имеет более низкий [math]\displaystyle{ DP_{max} }[/math], ожидается, что фактическая верхняя граница [math]\displaystyle{ DCP }[/math] будет ниже, чем приведённая выше оценка. В результате мы считаем, что полный цикл CLEFIA защищён от дифференциального криптоанализа (в CLEFIA используется 18 раундов).

Линейный криптоанализ

Для оценки сложности линейного криптоанализа применяется подход на основе подсчёта активных S-блоков при заданном количестве раундов. Поскольку [math]\displaystyle{ LP^{S_0}_{max} = 2^{-4.38} }[/math], используя 30 активных S-блоков для 12-раундового CLEFIA, [math]\displaystyle{ LCP^{12r}_{max} \le 2^{30 \cdot (-4.38)} = 2^{-131.40} }[/math]. Это даёт вывод, что злоумышленнику трудно найти достаточное количество пар текст-шифротекст, которые можно использовать для успешной атаки на CLEFIA. В результате полнофункциональный CLEFIA достаточно защищён от линейного криптоанализа.

Невозможный дифференциальный криптоанализ

Считается, что невозможная дифференциальная атака является одной из самых мощных атак против CLEFIA. Найдены следующие два невозможных дифференциальных пути:

[math]\displaystyle{ (0,\alpha,0,0)\overset{9r}{\nrightarrow}(0,\alpha,0,0)\ \mbox{и} \ (0,0,0,\alpha)\overset{9r}{\nrightarrow}(0,0,0,\alpha)\quad p=1 }[/math]

где [math]\displaystyle{ \alpha \in \{0, 1\}^{32} }[/math] — любая ненулевая величина. Таким образом, используя описанный выше отличительный признак, можно смоделировать атаку (для каждой длины ключа), которая будет восстанавливать текущий ключ. В следующей таблице приведены данные о сложностях, необходимых для невозможных дифференциальных атак. Согласно этой таблице ожидается, что у CLEFIA с полным циклом есть достаточный запас безопасности против этой атаки.

Трудоёмкость невозможного дифференциального криптоанализа

Количество раундов	Длина ключа	Ключевое забеливание	Количество открытых текстов	Временная сложность
10	128,192,256	+	[math]\displaystyle{ 2^{101.7} }[/math]	[math]\displaystyle{ 2^{102} }[/math]
11	192,256	+	[math]\displaystyle{ 2^{103.5} }[/math]	[math]\displaystyle{ 2^{188} }[/math]
12	256	-	[math]\displaystyle{ 2^{103.8} }[/math]	[math]\displaystyle{ 2^{252} }[/math]

Сравнение с другими шифрами

CLEFIA обеспечивает компактную и быструю реализацию одновременно без ущерба для безопасности. По сравнению с AES, наиболее широко используемым 128-битным блочным шифром, CLEFIA имеет преимущество в аппаратной реализации. CLEFIA может реализовывать скорость 1,6 Гбит/с с площадью менее 6 тысяч эквивалентных логических ячеек, а пропускная способность на шлюз является самой высокой в мире на 2008 год (в случае аппаратной реализации).

В таблице ниже приведена сравнительная характеристика шифра CLEFIA по отношению к некоторым другим известным шифрам:

Реализация с оптимизацией по площади

Алгоритм	Размер блока(биты)	Размер ключа(биты)	Количество раундов	Пропускная способность(Mpbs)	Площадь (Kgates)	Эффективность (Kpbs/gates)
CLEFIA	128	128	18	1,605.94	5.98	268.63
			36	715.69	4.95	144.59
AES	128	128	10	3,422.46	27.77	123.26
Camellia	128	128	23	1,488.03	11.44	130.11
SEED	128	128	16	913.24	16.75	54.52
			52	517.13	9.57	54.01
CAST-128	64	128	17	386.12	20.11	19.20
MISTY1	64	128	9	915.20	14.07	65.04
			30	570.41	7.92	72.06
TDEA	64	56, 112, 168	48	355.56	3.76	94.50

Реализация с оптимизацией по скорости

Алгоритм	Размер блока(биты)	Размер ключа(биты)	Количество раундов	Пропускная способность(Mpbs)	Площадь (Kgates)	Эффективность (Kpbs/gates)
CLEFIA	128	128	18	3,003.00	12.01	250.06
			36	1,385.10	9.38	147.71
AES	128	128	10	7,314.29	45.90	159.37
Camellia	128	128	23	2,728.05	19.95	136.75
SEED	128	128	16	1,556.42	25.14	61.90
			52	898.37	12.33	72.88
CAST-128	64	128	17	909.35	33.11	27.46
MISTY1	64	128	9	1,487.68	17.22	86.37
			30	772.95	10.12	76.41
TDEA	64	56, 112, 168	48	766.28	5.28	145.10

Применение

В 2019 году организации ISO и IEC включили алгоритмы PRESENT и CLEFIA в международный стандарт облегчённого шифрования ISO/IEC 29192-2:2019.

Существует библиотека CLEFIA_H на языке программирования C, реализующая шифр CLEFIA.

Ссылки

• CLEFIA веб-сайт (англ.)
• Sony Introduces CLEFIA (англ.)
• Differential Improved Impossible Cryptanalysis of CLEFIA (англ.)
• Реализация библиотеки CLEFIA_H на языке C (англ.)
• Пример реализации алгоритма на языке C
• Пример реализации кодека и хэш-функции CLEFIA на языке С