XXTEA

XXTEA
Создатель	Дэвид Вилер и Роджер Нидхэм
Создан	1998 г.
Опубликован	1998 г.
Размер ключа	128 бит
Размер блока	[math]\displaystyle{ n*32 }[/math] бит, где [math]\displaystyle{ n }[/math] - количество слов, не меньшее 2
Число раундов	[math]\displaystyle{ 6*n+52 }[/math], где [math]\displaystyle{ n }[/math] - количество слов
Тип	Сеть Фейстеля

XXTEA — криптографический алгоритм, реализующий блочное симметричное шифрование и представляющий собой сеть Фейстеля. Является расширение алгоритма Block TEA. Разработан и опубликован Дэвидом Уилером и Роджером Нидхемом в 1998 году. Выполнен на простых и быстрых операциях: XOR, подстановка, сложение.

История

На симпозиуме Fast Software Encryption в декабре 1994 года Дэвид Уилер и Роджер Нидхэм, профессора́ Компьютерной Лаборатории Кембриджского Университета, представили новый криптографический алгоритм TEA. Данный алгоритм проектировался как альтернатива DES, который к тому моменту уже считался устаревшим.

Позже в 1996 году в ходе личной переписки Дэвида Уилера с Дэвидом Вагнером была выявлена уязвимость для атаки на связанных ключах, которая была официально представлена в 1997 году на Первой Международной Конференции ICIS группой учёных, состоявшей из Брюса Шнайера, Джона Келси и Дэвида Вагнера. Данная атака послужила основанием для улучшения алгоритма TEA, и в октябре 1996 года Уилер и Нидхэм опубликовали внутренний отчет лаборатории, в котором приводилось два новых алгоритма: XTEA и Block TEA.

10 октября 1998 года группа новостей sci.crypt.research опубликовала статью Маркку-Юхани Сааринена, в которой была найдена уязвимость Block TEA на стадии дешифрования. В том же месяце Дэвид Уилер и Роджер Нидхэм опубликовали внутренний отчёт лаборатории, в котором приводилось улучшение алгоритма Block TEA — XXTEA.

Особенности

XXTEA, как и остальные шифры семейства TEA, обладает рядом отличительных особенностей по сравнению с аналогичными шифрами:

• Высокая скорость работы
• Малое потребление памяти
• Простая программная реализация
• Относительно высокая надёжность.

Описание работы алгоритма

Схема алгоритма шифрования XXTEA

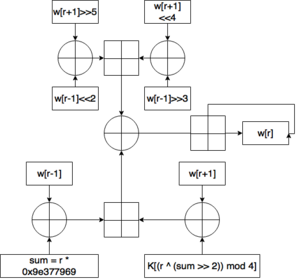
Исходный текст разбивается на слова по 32 бита каждый, из полученных слов формируется блок. Ключ также разбивают на 4 части, состоящие из слов по 32 бита каждый, и формируют массив ключей. В ходе одного раунда работы алгоритма шифруется одно слово из блока. После того, как были зашифрованы все слова, заканчивается цикл, и начинается новый. Количество циклов зависит от количества слов и равно [math]\displaystyle{ 6+52/n }[/math], где [math]\displaystyle{ n }[/math] — количество слов. Шифрование одного слова состоит в следующем:

1. Над левым соседом выполняется операция битового сдвига влево на два, а над правым операция битового сдвига вправо на пять. Над полученными значениями выполняют операцию побитового сложения по модулю 2.
2. Над левым соседом выполняется операция битового сдвига вправо на три, а над правым операция битового сдвига влево на 4. Над полученными значениями выполняют операцию побитового сложения по модулю 2
3. Полученные числа складывают по модулю 2³².
4. Константа δ, выведенная из Золотого сечения δ = ([math]\displaystyle{ \sqrt{5} }[/math] — 1) * 2³¹ = 2654435769 = 9E3779B9_h, умножается на номер цикла(это было сделано для предотвращения простых атак, основанных на симметрии раундов).
5. Полученное в предыдущем пункте число складывают побитово по модулю 2 с правым соседом.
6. Полученное в 4 пункте число сдвигают побитово направо на 2, складывают побитово по модулю два с номером раунда и находят остаток от деления на 4. С помощью полученного числа выбирают ключ из массива ключей.
7. Выбранный в предыдущем раунде ключ складывают побитово по модулю 2 с левым соседом.
8. Числа, полученные в предыдущем и 4 пунктах, складывают по модулю 2³².
9. Числа, полученные в предыдущем и 3 пунктах, складывают побитово по модулю 2, данную сумму складывают с шифруемым словом по модулю 2³².

Криптоанализ

На данный момент существует атака на основе адаптивно подобранного открытого текста, опубликованная Элиас Яаррков в 2010 году. Существует два подхода, в которых используется уменьшение количества циклов за счет увеличения количества слов.

Первый подход

Схема первого подхода дифференциального криптоанализа XXTEA

Пусть у нас есть некий открытый текст. Возьмем из него 5 неких слов, начиная с [math]\displaystyle{ r }[/math], которые мы шифруем с [math]\displaystyle{ r+1 }[/math]. Прибавим какое-нибудь число к [math]\displaystyle{ r+2 }[/math], и получим новый открытый текст. Теперь выполним первый цикл шифрования для этих текстов. Если после шифрования разница осталась только в данном слове, то продолжаем шифрование. Если начали появляться разницы в других словах, то начинаем поиск заново либо меняя исходный, либо пытаясь подобрать другую разницу. Сохранение разницы только в одном слове возможно, так как функция шифрования не биективна для каждого соседа. Элиас Яаррков провел ряд экспериментов и выяснил, что вероятность прохождения разности [math]\displaystyle{ \Delta=13 }[/math] 5 полных циклов давала вероятность между [math]\displaystyle{ 2 }[/math]^{[math]\displaystyle{ -109 }[/math]} и [math]\displaystyle{ 2 }[/math]^{[math]\displaystyle{ -110 }[/math]} для большинства ключей, то есть если пара текстов прошла 5 из 6 полных циклов, то её можно считать верной, так как если поместить разницу в конец блока, будут возникать разницы в большинстве слов. Данная атака была проведена и был восстановлен ключ для алгоритма с количеством циклов уменьшенным до трёх.

Второй подход

Схема второго подхода дифференциального криптоанализа XXTEA

Второй подход отличается от первого тем, что после первого раунда шифрования [math]\displaystyle{ r+1 }[/math] слова, разница должна перейти в него самого из [math]\displaystyle{ r+2 }[/math] слова, при этом разница может измениться, а после следующего раунда шифрования разница вернется в [math]\displaystyle{ r+2 }[/math] слово и станет равна изначальному, но изменит знак. После проведения оценки данного метода, Элиас Яаррков получил, что для успешного нахождения правильной пары достаточно 2⁵⁹ текстов, причем разница должна лежать в интервале [math]\displaystyle{ [-d;d] }[/math], где [math]\displaystyle{ d=32 }[/math], причем увеличение d не улучшило результатов. После была проведена успешная атака на XXTEA с количеством циклом, уменьшенным до 4, и правильная пара была получена с помощью 2³⁵ пар текстов, а предыдущая оценка даёт необходимость в 2^34.7 пар текстов.

Восстановление ключа

Зная правильную пару текстов, достаточно прогнать алгоритм в обратном порядке, так как теперь нам известно все кроме ключа.

Литература

• David J. Wheeler, Roger M. Needham. Correction to XTEA (англ.). — 1998. — Октябрь.
• E. Yarrkov. Cryptanalysis of XXTEA (англ.). — 2010. — 4 Май.
• Saarinen M.-J. Cryptanalysis of Block Tea (англ.). — 1998. — 20 Октябрь.
• David J. Wheeler, Roger M. Needham. TEA, a tiny encryption algorithm (англ.). — 1994. — Декабрь.
• David J. Wheeler, Roger M. Needham. TEA extensions (англ.). — 1996. — Октябрь.
• J. Kelsey, B. Schneier and D. Wagner. Related-key cryptanalysis of 3-WAY, Biham-DES,CAST, DES-X, NewDES, RC2, and TEA (англ.). — 1997. — Ноябрь.
• Mao Cenwei. Comparison of a Few Small Ciphers Applicable to RFID (англ.). — 2008. — Июнь.
• I. Sima, D. Tarmurean и V. Greu. XXTEA, an alternative replacement of KASUMI cipher algorithm in A5/3 GSM and f8, f9 UMTS data security functions (англ.). — 2012. — Июнь.
• First International Conference, ICIS'97, Beijing, China, November 11-14, 1997, Proceedings / Editors: Yongfei Han, Tatsuaki Okamoto, Sihan Quing. — 1. — Springer-Verlag Berlin Heidelberg, 1997. — (Lecture Notes in Computer Science). — ISBN 978-3-540-63696-0.