SQUARE

SQUARE
Создатель	Винсент Рэймен, Йоан Даймен, Ларс Кнудсен
Создан	1997
Опубликован	1997
Размер ключа	128 бит
Размер блока	128 бит
Число раундов	8
Тип	Подстановочно-перестановочная сеть

SQUARE — в криптографии симметричный блочный криптоалгоритм, разработанный в 1997 году Винсентом Рэйменом, Йоаном Дайменом и Ларсом Кнудсеном.

Считается предшественником алгоритма AES. Структура алгоритма была подобрана авторами для возможности получения эффективной реализации на широком спектре процессоров, а также для криптостойкости к дифференциальному и линейному криптоанализу.

Описание алгоритма

Алгоритм SQUARE использует ключ длиной 128 бит, данные шифруются 128-битными блоками, однако модульный подход к построению шифра позволяет легко расширить до больших размеров длину ключа и длину блока данных. Один раунд SQUARE состоит из четырёх отдельных преобразований. Данные представляются байтовым квадратом размера 4x4. Основные составляющие этого шифра — это пять различных обратимых преобразований, которые воздействуют на массив байтов размера [math]\displaystyle{ 4 \times 4 }[/math].

Преобразования в раунде шифрования

Линейное преобразование [math]\displaystyle{ \theta }[/math]

Линейное преобразование [math]\displaystyle{ \theta }[/math] воздействует на каждую строку в квадрате данных. Оно представляется формулой [math]\displaystyle{ {b_{i,j} = c_ja_{i,0} \oplus c_{j-1}a_{i,1} \oplus c_{j-2}a_{i,2} \oplus c_{j-3}a_{i,3} } }[/math], где:

• [math]\displaystyle{ {a_{i,j}} }[/math] — значение байта, находящегося в [math]\displaystyle{ i }[/math]-й строке и [math]\displaystyle{ j }[/math]-м столбце в квадрате данных;
• [math]\displaystyle{ {b_{i,j}} }[/math] — новое значение байта в квадрате;
• [math]\displaystyle{ {c_n} }[/math] — набор констант;
• умножения выполняются в поле Галуа [math]\displaystyle{ {GF(2^8)} }[/math];

Важно, что поле [math]\displaystyle{ {GF(2^8)} }[/math] имеет характеристику 2, то есть операция сложения соответствует побитовому [math]\displaystyle{ \mathrm{xor} }[/math]. Каждая [math]\displaystyle{ i }[/math]-ая строка в квадрате может быть представлена в виде полинома [math]\displaystyle{ a_i(x) = a_{i,0} \oplus a_{i,1}x \oplus a_{i,2}x^2 \oplus a_{i,3}x^3 }[/math]. Тогда, определяя коэффициенты [math]\displaystyle{ {c_n} }[/math] как полином [math]\displaystyle{ {c(x) = \oplus _j c_jx^j} }[/math], преобразование [math]\displaystyle{ \theta }[/math] можно представить в виде произведения полиномов: [math]\displaystyle{ b_i(x) = c(x)a_i(x) \mod 1 \oplus x^4 }[/math], здесь [math]\displaystyle{ b_i(x) }[/math] — новое значение строки квадрата, представленное в виде полинома, и [math]\displaystyle{ c(x) = 2\oplus 1\cdot x\oplus 1\cdot x^2\oplus 3\cdot x^3 }[/math] . Обратному преобразованию [math]\displaystyle{ \theta^{-1} }[/math] соответствует полином [math]\displaystyle{ d(x) }[/math], определённый по формуле [math]\displaystyle{ c(x)d(x)= 1 \pmod 1 \oplus x^4 }[/math].

Нелинейное преобразование [math]\displaystyle{ \gamma }[/math]

Данное преобразование является табличной заменой [math]\displaystyle{ \gamma }[/math]. Таблица, по которой осуществляется замена:

B1

CE

C3

95

5A

AD

E7

02

4D

44

FB

91

0C

87

A1

50

CB

67

54

DD

46

8F

E1

4E

F0

FD

FC

EB

F9

C4

1A

6E

5E

F5

CC

8D

1C

56

43

FE

07

61

F8

75

59

FF

03

22

8A

D1

13

EE

88

00

0E

34

15

80

94

E3

ED

B5

53

23

4B

47

17

A7

90

35

AB

D8

B8

DF

4F

57

9A

92

DB

1B

3C

C8

99

04

8E

E0

D7

7D

85

BB

40

2C

3A

45

F1

42

65

20

41

18

72

25

93

70

36

05

F2

0B

A3

79

EC

08

27

31

32

B6

7C

B0

0A

73

5B

7B

B7

81

D2

0D

6A

26

9E

58

9C

83

74

B3

AC

30

7A

69

77

0F

AE

21

DE

D0

2E

97

10

A4

98

A8

D4

68

2D

62

29

6D

16

49

76

C7

E8

C1

96

37

E5

CA

F4

E9

63

12

C2

A6

14

BC

D3

28

AF

2F

E6

24

52

C6

A0

09

BD

8C

CF

5D

11

5F

01

C5

9F

3D

A2

9B

C9

3B

BE

51

19

1F

3F

5C

B2

EF

4A

CD

BF

BA

6F

64

D9

F3

3E

B4

AA

DC

D5

06

C0

7E

F6

66

6C

84

71

38

B9

1D

7F

9D

48

8B

2A

DA

A5

33

82

39

D6

78

86

FA

E4

2B

A9

1E

89

60

6B

EA

55

4C

F7

E2

Преобразование [math]\displaystyle{ \pi }[/math]

то есть 0 заменится на B1, 1 — на CE, и так далее.

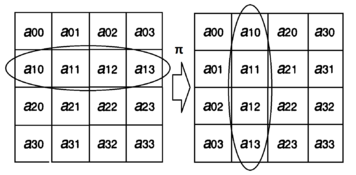
Байтовая перестановка [math]\displaystyle{ \pi }[/math]

Байтовая перестановка осуществляет транспонирование байтового квадрата, то есть [math]\displaystyle{ {a_{i,j}=a_{j,i}} }[/math].

Сложение с ключом раунда [math]\displaystyle{ \sigma[K_i] }[/math]

Эта операция — побитовое сложение 128 бит данных с ключом раунда, [math]\displaystyle{ {b=a\oplus K_i} }[/math], где:

• [math]\displaystyle{ {a} }[/math] и [math]\displaystyle{ {b} }[/math] — значение 128 бит данных перед преобразованием и после;
• [math]\displaystyle{ {K_i} }[/math] — ключ раунда [math]\displaystyle{ {i} }[/math].

Процедура получения ключей

Для шифрования необходимо получить 8 128-битных ключей раундов, а также ключ для предварительного раунда из ключа шифрования алгоритма.

Процедура [math]\displaystyle{ \psi }[/math] получения ключей.

Процедура получения ключа описывается преобразованием [math]\displaystyle{ \psi: K_{i+1} = \psi(K_{i}) }[/math], выполняющимся над ключом, представленным, как и блок данных, байтовым квадратом 4x4. Преобразование [math]\displaystyle{ \psi }[/math] описывается следующими операциями:

• [math]\displaystyle{ {k_{0,i+1} = k_{0,i}\oplus rotl(k_{3,i})\oplus C_i} }[/math];
• [math]\displaystyle{ {k_{1,i+1} = k_{1,i}\oplus k_{0,i+1}} }[/math];
• [math]\displaystyle{ {k_{2,i+1} = k_{2,i}\oplus k_{1,i+1}} }[/math];
• [math]\displaystyle{ {k_{3,i+1} = k_{3,i}\oplus k_{2,i+1}} }[/math];

где:

• [math]\displaystyle{ {k_{n,i}} }[/math] — [math]\displaystyle{ n }[/math]-я строка байтового квадрата ключа [math]\displaystyle{ i }[/math]-го раунда;
• [math]\displaystyle{ C_i }[/math] — константа для [math]\displaystyle{ i }[/math]-го раунда, вычисляемая по формуле [math]\displaystyle{ {C_{i+1} = 2\cdot C_{i}} }[/math], [math]\displaystyle{ C_0 = 1 }[/math];
• [math]\displaystyle{ {rotl()} }[/math] — операция циклического сдвига байтовой строки на один байт влево: [math]\displaystyle{ rotl[a_{i,0},a_{i,1},a_{i,2},a_{i,3}] = [a_{i,1},a_{i,2},a_{i,3},a_{i,0}] }[/math];

Исходный ключ алгоритма шифрования используется как ключ для предварительного раунда.

Шифрование

Обозначим один раунд шифрования как [math]\displaystyle{ \rho[k^t] = \sigma[k^t] \circ \pi \circ \gamma \circ \theta }[/math]. Также, восьми раундам преобразования предшествует сложение с ключом [math]\displaystyle{ \sigma[K_0] }[/math] и [math]\displaystyle{ \theta^{-1} }[/math]:[math]\displaystyle{ \mathrm{Square}[k] = \rho[k^8] \circ \rho[k^7] \circ \rho[k^6] \circ \rho[k^5] \circ \rho[k^4] \circ \rho[k^3] \circ \rho[k^2] \circ \rho[k^1] \circ \sigma[k^0] \circ \theta^{-1} }[/math].

Расшифрование

Алгоритм расшифрования аналогичен алгоритму шифрования, но вместо преобразований [math]\displaystyle{ \gamma }[/math] и [math]\displaystyle{ \theta }[/math] используются обратные преобразования [math]\displaystyle{ \gamma^{-1} }[/math] и [math]\displaystyle{ \theta^{-1} }[/math], при этом [math]\displaystyle{ \gamma^{-1} }[/math] — это обратная табличная замена, а [math]\displaystyle{ \theta^{-1} }[/math] — это умножение строки на полином [math]\displaystyle{ d(x) }[/math] такой, что [math]\displaystyle{ d(x)c(x) = 1\pmod {1 \oplus x^4} }[/math], также в предварительном раунде используется преобразование [math]\displaystyle{ \theta }[/math] вместо [math]\displaystyle{ \theta^{-1} }[/math]. Из формулы для шифрования видно, что

[math]\displaystyle{ \mathrm{Square^{-1}}[k] = \theta \circ \sigma^{-1}[k^0] \circ \rho^{-1}[k^1] \circ \rho^{-1}[k^2] \circ \rho^{-1}[k^3] \circ \rho^{-1}[k^4] \circ \rho^{-1}[k^5] \circ \rho^{-1}[k^6] \circ \rho^{-1}[k^7] \circ \rho^{-1}[k^8] }[/math],

где [math]\displaystyle{ \rho^{-1}[k^t] = \theta^{-1} \circ \gamma^{-1} \circ \pi^{-1} \circ \sigma^{-1}[k^t] = \theta^{-1} \circ \gamma^{-1} \circ \pi \circ \sigma[k^t] }[/math]. Так как [math]\displaystyle{ \gamma^{-1} \circ \pi = \pi \circ \gamma^{-1} }[/math], и, более того, так как [math]\displaystyle{ \theta^{-1}(a) \oplus k^t = \theta^{-1}(a + \theta(k^t)) }[/math], получаем [math]\displaystyle{ \sigma[k^t] \circ \theta^{-1} = \theta^{-1}\circ\sigma[\theta(k^t)] }[/math]. Теперь один раунд для расшифрования можно определить как [math]\displaystyle{ \rho'[k^t] = \sigma[k^t]\circ\pi\circ\gamma^{-1}\circ\theta^{-1} }[/math], и полная формула для расшифрования записывается как :

[math]\displaystyle{ \mathrm{Square}^{-1} = \rho'[k^8] \circ \rho'[k^7] \circ \rho'[k^6] \circ \rho'[k^5] \circ \rho'[k^4] \circ \rho'[k^3] \circ \rho'[k^2] \circ \rho'[k^1] \circ \sigma[k^0] \circ \theta }[/math].

Безопасность

Исследование криптостойкости создателями алгоритма

Алгоритм обладает высокой стойкостью против линейного и дифференциального криптоанализа, благодаря преобразованиям [math]\displaystyle{ \theta }[/math] и [math]\displaystyle{ \gamma }[/math], которые понижают максимальную вероятность появления дифференциальных следов и максимальную корреляцию линейных следов за 4 раунда преобразований. Первый криптоанализ SQUARE был проведён его авторами с использованием интегрального криптоанализа, который позже стал известен как Square-атака.

Описание Square-атаки

Прежде всего, введем несколько определений:

Определение 1: Пусть [math]\displaystyle{ \Lambda }[/math]-множество — набор из 256 16-байтовых состояний, каждое из которых отличается от других в некоторых байтах, которые назовём активными, и совпадают в некоторых байтах, которые будем называть пассивными. Далее, [math]\displaystyle{ \lambda }[/math] — это набор индексов активных байтов. Имеем:

[math]\displaystyle{ \forall x, y \in \Lambda : \begin{cases} x_{i,j}\ne y_{i,j}, for (i,j)\in \lambda \\ x_{i,j} = y_{i,j}, for (i,j)\notin \lambda \end{cases} }[/math].

Определение 2: Если применение операции исключающего «или» ко всем байтам на одной позиции в [math]\displaystyle{ \Lambda }[/math]-множестве даёт 0, то эта позиция называется уравновешенной по [math]\displaystyle{ \Lambda }[/math]-множеству.

Применение преобразований [math]\displaystyle{ \gamma }[/math] и [math]\displaystyle{ \sigma[k^t] }[/math] к [math]\displaystyle{ \Lambda }[/math]-множеству даёт [math]\displaystyle{ \Lambda }[/math]-множество с тем же [math]\displaystyle{ \lambda }[/math]. Применение преобразования [math]\displaystyle{ \pi }[/math] даёт [math]\displaystyle{ \Lambda }[/math]-множество, в котором активные байты транспонированы (относительно активных байтов в исходном [math]\displaystyle{ \Lambda }[/math]-множестве). Также, применение [math]\displaystyle{ \theta }[/math] к [math]\displaystyle{ \Lambda }[/math]-множеству необязательно вернёт [math]\displaystyle{ \Lambda }[/math]-множество, однако, так как каждый выходной байт [math]\displaystyle{ \theta }[/math] является линейной комбинацией четырёх входных байт в той же строке, то, подавая строку с всего одним активным байтом, на выходе получим строку состоящую только из активных байт. Рассмотрим [math]\displaystyle{ \Lambda }[/math]-множество, в котором только один байт является активным и проследим, как изменяется позиция активного байта в течение трех раундов (здесь предварительный раунд объединён с первым: [math]\displaystyle{ \rho[k^1] \circ \sigma[k^0] \circ \theta^{-1} }[/math], который в итоге записывается как [math]\displaystyle{ \sigma[k^1]\circ\pi\circ\gamma\circ\theta\circ\sigma[k^0]\circ\theta^{-1} = \sigma[k^1]\circ\pi\circ\gamma\circ\sigma[\theta(k^0)] }[/math]). Так как первый раунд не содержит [math]\displaystyle{ \theta }[/math], то к началу второго раунда остается один активный байт. Во втором раунде [math]\displaystyle{ \theta }[/math] преобразует в строку активных байтов, которые [math]\displaystyle{ \pi }[/math] преобразует в столбец активных байт. [math]\displaystyle{ \theta }[/math] в третьем раунде переводит результат в [math]\displaystyle{ \Lambda }[/math]-множество, состоящее только из активных байт. Значения байт на выходе третьего раунда пробегают все возможные значения, следовательно, уравновешены по множеству [math]\displaystyle{ \Lambda }[/math], имеем

[math]\displaystyle{ \underset{b=\theta(a), a\in\Lambda}{\bigoplus} b_{i,j} = \underset{a\in\Lambda}{\bigoplus} \underset{k}{\bigoplus} c_{j-k}a_{i,k} = \underset{l}{\bigoplus}c_l \underset{a\in\Lambda}{\bigoplus} a_{i,l+j} = \underset{l}{\bigoplus}c_l 0 = 0, }[/math]

значит байты на выходе [math]\displaystyle{ \theta }[/math] в четвёртом раунде уравновешены по [math]\displaystyle{ \Lambda }[/math]-множеству. Эта уравновещенность нарушается последующим применением [math]\displaystyle{ \gamma }[/math]. Выходные байты четвёртого раунда могут быть выражены с помощью функции от промежуточного состояния [math]\displaystyle{ b }[/math]: [math]\displaystyle{ a_{i,j} = S_\gamma[b_{j, i}]\oplus k^4 _{i,j} }[/math]. Предполагая значение [math]\displaystyle{ k^4 _{i,j} }[/math], значение [math]\displaystyle{ b_{j,i} }[/math] для всех элементов [math]\displaystyle{ \Lambda }[/math]-множества могут быть вычислены из шифротекстов. Если значение этого байта оказалось неуравновешенным по [math]\displaystyle{ \Lambda }[/math], то предположенное значение ключа [math]\displaystyle{ k^4 _{i,j} }[/math] является ложным. Этот метод криптоанализа позволил взломать 6-раундовый вариант шифра с использованием [math]\displaystyle{ 2^{32} }[/math] блоков открытого текста и соответствующих им блоков шифротекста и выполнением [math]\displaystyle{ 2^{72} }[/math] операций шифрования.

В 2010 году была представлена атака на связанных ключах методом бумеранга. Ранее подобная атака применялась к шифрам KASUMI, COCONUT98, IDEA и AES-192/256. Это была первая атака на полнораундовый SQUARE. В 2011 году был проведён криптоанализ полнораундового варианта SQUARE с помощью полного двудольного графа. Данный тип атаки позволил взломать шифр с использованием одного ключа, [math]\displaystyle{ 2^{48} }[/math] открытых текстов и проведения [math]\displaystyle{ 2^{126} }[/math] операций шифрования.

Особенности шифра

Шифр SQUARE создавался, соответствуя стратегии широкого следа — каждый раунд шифра состоит из нескольких преобразований, нелинейной перестановки и композиции линейных преобразований — что дало шифру высокую криптостойкость против линейного и дифференциального криптоанализа. Составляющие блоки алгоритма и их взаимодействие подбирались также исходя из возможности быстрой реализации на широком спектре процессоров. Реализация алгорима на языке Си имела скорость шифрования 2.63 Мбайт/с, запускаемая на процессоре Pentium с частотой 100 МГц, а реализация на языке Ассемблер увеличивала скорость шифрования вдвое. Данный алгоритм получил развитие и стал основой нового американского стандарта — шифра Rijndael, который был разработан группой авторов SQUARE. Кстати, на конкурсе AES, эксперты отметили, что «в основе алгоритма Rijndael лежит нетрадиционная парадигма, поэтому он может содержать скрытые уязвимости». Именно по этой причине сам SQUARE сейчас используется редко, уступая в популярности своему потомку — Rijndael. Также потомком шифра является южнокорейский алгоритм CRYPTON, участник конкурса AES.

См. также

• Rijndael

Литература

• J. Daemen, L. Knudsen, V. Rijmen. The Block Cipher SQUARE. — 1997.
• B. Koo, Y. Yeom, J. Song. Related-Key Boomerang Attack on Block Cipher SQUARE. — 2010.
• H. Mala. Biclique Cryptanalisis of the Block Cipher SQUARE. — 2011.
• G.Piret, J.-J. Quisquater. Impossible differential and square attacks: Cryptanalytic link and application to Skipjack. — 2001.
• Шаблон:Source

Ссылки

• The Block Cipher Square Algorithm, Joan Daemen, Lars R. Knudsen and and Vincent Rijmen, Dr. Dobb’s Journal, October 01, 1997.