Отрицательное биномиальное распределение
| Отрицательное биномиальное распределение | |
|---|---|
 Функция вероятности Функция вероятности | |
| Обозначение | [math]\displaystyle{ \mathrm{NB}(r,p) }[/math] |
| Параметры |
[math]\displaystyle{ r \gt 0 }[/math] [math]\displaystyle{ p \in (0;1) }[/math] [math]\displaystyle{ q\equiv 1-p }[/math] |
| Носитель | [math]\displaystyle{ k \in \{0,1,2,\ldots\} }[/math] |
| Функция вероятности | [math]\displaystyle{ \frac{\Gamma(r+k)}{k!\,\Gamma(r)}\,p^r\,q^k }[/math] |
| Функция распределения | [math]\displaystyle{ I_p(r,k+1) }[/math] |
| Математическое ожидание | [math]\displaystyle{ \frac{rq}{p} }[/math] |
| Мода |
[math]\displaystyle{ \left\lfloor\frac{(r-1)q}{p}\right\rfloor }[/math] если [math]\displaystyle{ \ r\gt 1 \ }[/math] [math]\displaystyle{ 0 }[/math] если [math]\displaystyle{ r\leq1 }[/math] |
| Дисперсия | [math]\displaystyle{ \frac{rq}{p^2} }[/math] |
| Коэффициент асимметрии | [math]\displaystyle{ \frac{2-p}{\sqrt{r\,q}} }[/math] |
| Коэффициент эксцесса | [math]\displaystyle{ \frac{6}{r} + \frac{p^2}{r\,q} }[/math] |
| Производящая функция моментов | [math]\displaystyle{ \left(\frac{p}{1-q e^t}\right)^r }[/math] |
| Характеристическая функция | [math]\displaystyle{ \left(\frac{p}{1-q e^{i\,t}}\right)^r }[/math] |
Отрица́тельное биномиа́льное распределе́ние, также называемое распределением Паскаля — это распределение дискретной случайной величины, равной числу произошедших неудач в последовательности испытаний Бернулли с вероятностью успеха [math]\displaystyle{ p }[/math], проводимых до [math]\displaystyle{ r }[/math]-го успеха. Существуют алтернативные определения отрицательного биномиального распределения. Так оно может определяться как распределение дискретной случайной величины, равной числу испытаний по схеме Бернулли, каждое с вероятностью успеха [math]\displaystyle{ p }[/math], проводимых до [math]\displaystyle{ r }[/math]-го успеха.
Определение
Пусть [math]\displaystyle{ \{X_i\}_{i=1}^{\infty} }[/math] — последовательность независимых случайных величин с распределением Бернулли, то есть
- [math]\displaystyle{ X_i = \left\{ \begin{matrix} 1, & p \\ 0, & q \equiv 1-p \end{matrix} \right.,\; i\in \N. }[/math]
Построим случайную величину [math]\displaystyle{ Y }[/math] следующим образом. Пусть [math]\displaystyle{ k+r }[/math] — номер [math]\displaystyle{ r }[/math]-го успеха в этой последовательности. Тогда [math]\displaystyle{ Y = k }[/math]. Более строго, положим [math]\displaystyle{ S_n = \sum\limits_{i=1}^n X_i }[/math]. Тогда
- [math]\displaystyle{ Y = \inf\{n \mid S_n = r\} - r }[/math].
Распределение случайной величины [math]\displaystyle{ Y }[/math], определённой таким образом, называется отрицательным биномиальным. Пишут: [math]\displaystyle{ Y \sim \mathrm{NB}(r,p) }[/math].
Функции вероятности и распределения
Функция вероятности случайной величины [math]\displaystyle{ Y }[/math] имеет вид:
- [math]\displaystyle{ \mathbb{P}(Y = k) = \binom{k+r-1}{k}\, p^r q^k,\; k=0,1,2,\ldots }[/math].
Функция распределения [math]\displaystyle{ Y }[/math] кусочно-постоянна, и её значения в целых точках может быть выражено через неполную бета-функцию:
- [math]\displaystyle{ F_Y(k) = I_p( r, k+1 ) }[/math].
Отрицательное биномиальное распределение для [math]\displaystyle{ n }[/math] испытаний до [math]\displaystyle{ r }[/math]-го успеха
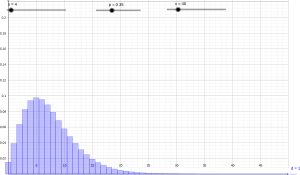
Это альтернативная формулировка отрицательного биномиального распределения. Если мы определяем отрицательное биномиальное распределение для [math]\displaystyle{ n }[/math] испытаний до [math]\displaystyle{ r }[/math]-го успеха, то функция вероятности будет равна:
- [math]\displaystyle{ f(n; r, p) \equiv \Pr(X = n) = \binom{n-1}{r-1} p^r(1-p)^{n-r} }[/math] [math]\displaystyle{ \text{для }n = r, r+1, r+2, \dotsc }[/math]
Так как для того, чтобы получить [math]\displaystyle{ r }[/math] успехов необходимо не менее [math]\displaystyle{ r }[/math] испытаний, то область значений [math]\displaystyle{ X=n }[/math] - от [math]\displaystyle{ r }[/math] до [math]\displaystyle{ \infty }[/math]. Если [math]\displaystyle{ X }[/math] обозначает количество испытаний для [math]\displaystyle{ r }[/math] успехов, [math]\displaystyle{ X_1 }[/math] - количество испытаний для первого успеха, [math]\displaystyle{ X_2 }[/math] для второго успеха, а [math]\displaystyle{ X_3 }[/math] - для третьего успеха, то общее количество испытаний для того чтобы получить [math]\displaystyle{ r }[/math] успехов равна:
- [math]\displaystyle{ X = X_1 + X_2 + X_3 }[/math].

Так как геометрическое распределение характеризуется отсутствием памяти, каждая случайная величина [math]\displaystyle{ X_1, X_2, X_3 }[/math] имеет геометрическое распределение и случайная величина отрицательного биномиального распределения является суммой [math]\displaystyle{ r }[/math] случайных величин геометрического распределения.
Отрицательная биномиальная случайная величина может рассматриваться как противоположность биномиальной случайной величины. В схеме Бернулли биномиальная случайная величина это количество успехов в [math]\displaystyle{ n }[/math] испытаниях, то есть количество испытаний заранее задано, а количество успехов случайно. Отрицательная биномиальная случайная величина это количество испытаний необходимое для получения [math]\displaystyle{ r }[/math] успехов, то есть количество успехов заранее задано, а количество испытаний случайно.
Моменты
Производящая функция моментов отрицательного биномиального распределения имеет вид:
- [math]\displaystyle{ M_Y(t) = \left(\frac{p}{1 - q e^t}\right)^r }[/math],
откуда математическое ожидание:
- [math]\displaystyle{ \mathbb{E}[Y] = \frac{rq}{p} }[/math],
- [math]\displaystyle{ \mathrm{D}[Y] = \frac{rq}{p^2} }[/math]
Свойства
Пусть [math]\displaystyle{ Y_i \sim NB(r_i,p) }[/math], тогда [math]\displaystyle{ \sum_i Y_i \sim NB\left(\sum_i r_i,p\right) }[/math]
Частные случаи отрицательного биномиального распределения
- При [math]\displaystyle{ r→∞ }[/math] отрицательное биномиальное распределение становится распределением Пуассона
- Если параметр [math]\displaystyle{ r }[/math] - целое число, то отрицательное биномиальное распределение становится обобщенным распределением Бозе-Эйнштейна [1].
- При [math]\displaystyle{ r=1 }[/math] отрицательное биномиальное распределение становится геометрическим распределением
- При [math]\displaystyle{ r=1 }[/math] получающееся геометрическое распределение является распределением Бозе-Эйнштейна для одного источника (a single source) [1].
Примечания
- ↑ 1,0 1,1 Schopper H. (Ed.) Electron - Positron Interactions. Berlin, Heidelberg: Springer-Verlag. 1992. P. 133// https://www.twirpx.org/file/3458790/ Архивная копия от 10 мая 2021 на Wayback Machine
Для улучшения этой статьи желательно: |