Многомерное нормальное распределение

Пример выборки из многомерного нормального распределения в пределах 3 сигм двух частных распределений

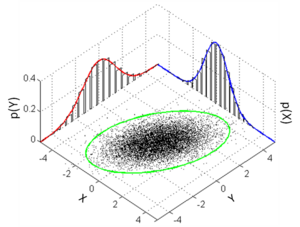
Многоме́рное норма́льное распределе́ние (или многоме́рное га́уссовское распределе́ние) в теории вероятностей — это обобщение одномерного нормального распределения. Случайный вектор, имеющий многомерное нормальное распределение, называется гауссовским вектором.

Определения

Случайный вектор [math]\displaystyle{ \mathbf{X} = (X_1,\ldots, X_n)^{\top}: \Omega \to \mathbb{R}^n }[/math] имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:

• Произвольная линейная комбинация компонентов вектора [math]\displaystyle{ \sum\limits_{i=1}^n a_i X_i }[/math] имеет нормальное распределение или является константой (это утверждение работает только если математическое ожидание равно 0).
• Существуют вектор независимых стандартных нормальных случайных величин [math]\displaystyle{ \mathbf{Z}=(Z_1,\ldots, Z_m)^{\top} }[/math], вещественный вектор [math]\displaystyle{ \mathbf{\mu} = (\mu_1,\ldots, \mu_n)^{\top} }[/math] и матрица [math]\displaystyle{ \mathbf{A} }[/math] размерности [math]\displaystyle{ n \times m }[/math], такие что:

[math]\displaystyle{ \mathbf{X} = \mathbf{A} \mathbf{Z} + \mathbf{\mu} }[/math].

• Существуют вектор [math]\displaystyle{ \mathbf{\mu} \in \mathbb{R}^n }[/math] и неотрицательно определённая симметричная матрица [math]\displaystyle{ \mathbf{\Sigma} }[/math] размерности [math]\displaystyle{ n \times n }[/math], такие что характеристическая функция вектора [math]\displaystyle{ \mathbf{X} }[/math] имеет вид:

[math]\displaystyle{ \phi_{\mathbf{X}}(\mathbf{u}) = e^{i \mathbf{\mu}^{\top} \mathbf{u} - \frac{1}{2}\mathbf{u}^{\top} \Sigma \mathbf{u}},\; \mathbf{u} \in \mathbb{R}^n }[/math].

Плотность невырожденного нормального распределения

• Если рассматривать только распределения с невырожденной ковариационной матрицей, то эквивалентным будет также следующее определение:

Существует вектор [math]\displaystyle{ \mathbf{\mu} \in \mathbb{R}^n }[/math] и положительно определённая симметричная матрица [math]\displaystyle{ \mathbf{\Sigma} }[/math] размерности [math]\displaystyle{ n \times n }[/math], такие что плотность вероятности вектора [math]\displaystyle{ \mathbf{X} }[/math] имеет вид::

[math]\displaystyle{ f_{\mathbf{X}}(\mathbf{x}) = \frac{1}{(2\pi )^{n/2} \vert \Sigma \vert^{1/2}} e^{-\frac{1}{2}(\mathbf{x} - \mathbf{\mu})^{\top} \Sigma^{-1} (\mathbf{x} - \mathbf{\mu})},\; \mathbf{x} \in \mathbb{R}^n }[/math],

где [math]\displaystyle{ \vert \Sigma\vert }[/math] — определитель матрицы [math]\displaystyle{ \Sigma }[/math], а [math]\displaystyle{ \Sigma^{-1} }[/math] — матрица обратная к [math]\displaystyle{ \Sigma }[/math]

• Вектор [math]\displaystyle{ \mathbf{\mu} }[/math] является вектором средних значений [math]\displaystyle{ \mathbf{X} }[/math], а [math]\displaystyle{ \Sigma }[/math] — его ковариационная матрица.
• В случае [math]\displaystyle{ n = 1 }[/math], многомерное нормальное распределение сводится к обычному нормальному распределению.
• Если случайный вектор [math]\displaystyle{ \mathbf{X} }[/math] имеет многомерное нормальное распределение, то пишут [math]\displaystyle{ \mathbf{X} \sim \mathcal{N}(\mathbf{\mu},\Sigma) }[/math].

Двумерное нормальное распределение

Частным случаем многомерного нормального распределения является двумерное нормальное распределение. В этом случае имеем две случайные величины [math]\displaystyle{ X_1, X_2 }[/math] с математическими ожиданиями [math]\displaystyle{ \mu_1, \mu_2 }[/math], дисперсиями [math]\displaystyle{ \sigma^2_1, \sigma^2_2 }[/math] и ковариацией [math]\displaystyle{ \sigma_{12} }[/math]. В этом случае ковариационная матрица имеет размер 2, её определитель равен

[math]\displaystyle{ \mathrm{det} \Sigma= \sigma^2_1 \sigma^2_2-\sigma^2_{12} =\sigma_1^2\sigma_2^2 (1-\rho^2), }[/math]

где [math]\displaystyle{ \rho = \frac{\sigma_{12}}{\sigma_1\sigma_2} }[/math] — коэффициент корреляции случайных величин.

Тогда плотность двумерного невырожденного (коэффициент корреляции по модулю не равен единице) нормального распределения можно записать в виде:

[math]\displaystyle{ f(x_1,x_2) = \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}} \exp \left\{ -\frac{1}{2(1-\rho^2)}\left[ \frac{(x_1-\mu_1)^2}{\sigma_1^2}-\rho \frac{2(x_1-\mu_1)(x_2-\mu_2)}{\sigma_1\sigma_2} +\frac{(x_2-\mu_2)^2}{\sigma_2^2}\right] \right\} }[/math].

В том случае, если [math]\displaystyle{ X \sim \mathcal{N}(\mu_1,\sigma^2_1), Y \sim \mathcal{N}(\mu_2,\sigma^2_2), cov(X,Y)=\sigma_{12} }[/math] (то есть [math]\displaystyle{ X, Y }[/math] являются зависимыми), их сумма все еще распределена нормально, но в дисперсии появляется дополнительное слагаемое [math]\displaystyle{ 2\sigma_{12} }[/math]: [math]\displaystyle{ X+Y \sim \mathcal{N}(\mu_1+\mu_2,\sigma^2_1+\sigma^2_2+2\sigma_{12}) }[/math].

Свойства многомерного нормального распределения

• Если вектор [math]\displaystyle{ \mathbf{X} = (X_1,\ldots, X_n)^{\top} }[/math] имеет многомерное нормальное распределение, то его компоненты [math]\displaystyle{ X_i, i=1,\ldots, n, }[/math] имеют одномерное нормальное распределение. Обратное верно при независимости компонент.
• Если случайные величины [math]\displaystyle{ X_1,\ldots,X_n }[/math] имеют одномерное нормальное распределение и совместно независимы, то случайный вектор [math]\displaystyle{ \mathbf{X} = (X_1,\ldots, X_n)^{\top} }[/math] имеет многомерное нормальное распределение. Матрица ковариаций [math]\displaystyle{ \Sigma }[/math] такого вектора диагональна.
• Если [math]\displaystyle{ \mathbf{X} = (X_1,\ldots, X_n)^{\top} }[/math] имеет многомерное нормальное распределение, и его компоненты попарно некоррелированы, то они независимы. Однако, если некоторые случайные величины [math]\displaystyle{ X_i,\; i = 1 , \ldots, n }[/math] имеют одномерные нормальные распределения и попарно не коррелируют, то отсюда не следует, что они независимы и имеют многомерное нормальное распределение.

Пример. Пусть [math]\displaystyle{ X \sim \mathcal{N}(0,1) }[/math], а [math]\displaystyle{ \alpha = \pm 1 }[/math] с равными вероятностями и независима от указанной нормальной величины. Тогда если [math]\displaystyle{ Y = \alpha X \sim \mathcal{N}(0,1) }[/math], то корреляция [math]\displaystyle{ X }[/math] и [math]\displaystyle{ Y }[/math] равна нулю. Однако, эти случайные величины зависимы и в силу первого утверждения абзаца не имеют многомерного нормального распредедения.

• Многомерное нормальное распределение устойчиво относительно линейных преобразований. Если [math]\displaystyle{ \mathbf{X} \sim \mathcal{N}(\mathbf{\mu},\Sigma) }[/math], а [math]\displaystyle{ \mathbf{A} }[/math] — произвольная матрица размерности [math]\displaystyle{ m \times n }[/math], то

[math]\displaystyle{ \mathbf{A}\mathbf{X} \sim \mathrm{N}\left(\mathbf{A}\mathbf{\mu},\mathbf{A}\Sigma \mathbf{A}^{\top}\right). }[/math]

Таким преобразованием и сдвигом любое невырожденное нормальное распределение можно привести к вектору независимых стандартных нормальных величин.

Моменты многомерного нормального распределения

Пусть [math]\displaystyle{ X }[/math] — центрированные (с нулевым математическим ожиданием) случайные величины имеющие многомерное нормальное распределение, тогда моменты [math]\displaystyle{ \mu_{i_1i_2i_3...i_k}=E(X_{i_1} X_{i_2}X_{i_3}...X_{i_k}) }[/math] для нечетных [math]\displaystyle{ k }[/math] равно нулю, а для четных [math]\displaystyle{ k=2m }[/math] вычисляется по формуле

[math]\displaystyle{ \sum \sigma_{i_{t_1}i_{t_2}}\sigma_{i_{t_3}i_{t_4}}\sigma_{i_{t_4}i_{t_5}}...\sigma_{i_{t_{k-1}}i_{t_k}} }[/math]

где суммирование осуществляется по всевозможным разбиениям индексов на пары. Количество множителей в каждом слагаемом равно [math]\displaystyle{ m }[/math], количество слагаемых равно [math]\displaystyle{ \frac {(2m)!}{2^{m}m!}=\frac {(2m-1)!}{2^{m-1}(m-1)!} }[/math]

Например, для моментов четвертого порядка в каждом слагаемом по два множителя и общее количество слагаемых будет равно [math]\displaystyle{ 4!/(2^2\cdot 2!)= (1\cdot 2\cdot 3\cdot 4)/(4\cdot 2\cdot 1)=3 }[/math]. Соответствующая общая формула для моментов четвертого порядка имеет вид:

[math]\displaystyle{ \mu_{ijkm}=E(X_{i} X_{j}X_{k}X_{m})=\sigma_{ij}\sigma_{km}+\sigma_{ik}\sigma_{jm}+\sigma_{im}\sigma_{kj} }[/math]

В частности если [math]\displaystyle{ i=j=k=m }[/math]

[math]\displaystyle{ \mu_{iiii}=E(X^4_i)=3 {\sigma}_{ii}^2=3{\sigma}_i^4 }[/math]

При [math]\displaystyle{ i=j\not = k=m }[/math]

[math]\displaystyle{ \mu_{iijj}=E(X^2_iX^2_j)={\sigma}_{ii}{\sigma}_{jj}+2{\sigma}_{ij}={\sigma}^2_{i}{\sigma}^2_{j}+2{\sigma}_{ij} }[/math]

При [math]\displaystyle{ i=j=k \not=m }[/math]

[math]\displaystyle{ \mu_{iiij}=E(X^3_iX_j)={\sigma}_{ii}{\sigma}_{ij}+{\sigma}_{ii}{\sigma}_{ij}+{\sigma}_{ij}{\sigma}_{ii}=3{\sigma}_{ij}{\sigma}_{ii}=3{\sigma}^2_{i}{\sigma}_{ij} }[/math]

Условное распределение

Пусть случайные векторы [math]\displaystyle{ X }[/math] и [math]\displaystyle{ Y }[/math] имеют совместное нормальное распределение с математическими ожиданиями [math]\displaystyle{ \mu_X, \mu_Y }[/math], ковариационными матрицами [math]\displaystyle{ V_X, V_Y }[/math] и матрицей ковариаций [math]\displaystyle{ C_{XY} }[/math]. Это означает, что объединенный случайный вектор [math]\displaystyle{ \boldsymbol Z = \begin{bmatrix} \boldsymbol X \\ \boldsymbol Y \end{bmatrix} }[/math] подчиняется многомерному нормальному распределению с вектором математического ожидания [math]\displaystyle{ \boldsymbol \mu_{Z} = \begin{bmatrix} \boldsymbol \mu_X \\ \boldsymbol \mu_Y \end{bmatrix} }[/math] и ковариационной матрицей, которую можно представить в виде следующей блочной матрицы

[math]\displaystyle{ \boldsymbol V_Z = \begin{bmatrix} \boldsymbol V_X & \boldsymbol C_{XY} \\ \boldsymbol C_{YX} & \boldsymbol V_{Y} \end{bmatrix} }[/math],

где [math]\displaystyle{ C_{YX}=C^T_{XY} }[/math].

Тогда случайный вектор [math]\displaystyle{ Y }[/math] при заданном значении случайного вектора [math]\displaystyle{ X }[/math] имеет (многомерное) нормальное условное распределение со следующим условным математическим ожиданием и условной ковариационной матрицей

[math]\displaystyle{ E(Y|X=x)=\mu_Y+C_{YX}V^{-1}_X(x-\mu_X), \qquad V(Y|X=x)=V_Y-C_{YX}V^{-1}_XC_{XY} }[/math].

Первое равенство определяет функцию линейной регрессии (зависимости условного математического ожидания вектора [math]\displaystyle{ Y }[/math] от заданного значения x случайного вектора [math]\displaystyle{ X }[/math]), причем матрица [math]\displaystyle{ C_{XY}V^{-1} }[/math] — матрица коэффициентов регрессии.

Условная ковариационная матрица представляет собой матрицу ковариаций случайных ошибок линейных регрессий компонентов вектора [math]\displaystyle{ Y }[/math] на вектор [math]\displaystyle{ X }[/math]. В случае если [math]\displaystyle{ Y }[/math] — обычная случайная величина (однокомпонентный вектор), условная ковариационная матрица — это условная дисперсия (по существу дисперсия случайной ошибки регрессии [math]\displaystyle{ Y }[/math] на вектор [math]\displaystyle{ X }[/math])

Литература

• М. де Гроот. Оптимальные статистические решения = Optimal Statistical Decisions. — М.: Мир, 1974. — 492 с.