Биномиальное распределение
| Биномиальное распределение | |
|---|---|
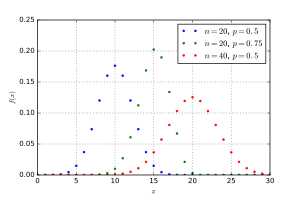 Функция вероятности Функция вероятности | |
 Функция распределения Функция распределения | |
| Обозначение | [math]\displaystyle{ B(n,p) }[/math] |
| Параметры |
[math]\displaystyle{ n \geqslant 0 }[/math] — число «испытаний» [math]\displaystyle{ 0\leqslant p \leqslant 1 }[/math] — вероятность «успеха» |
| Носитель | [math]\displaystyle{ k \in \{0,\dots,n\} }[/math] |
| Функция вероятности | [math]\displaystyle{ \binom{n}{k}\, p^k q^{n-k} }[/math] |
| Функция распределения | [math]\displaystyle{ I_{1-p}(n-\lfloor k\rfloor, 1+\lfloor k\rfloor) }[/math] |
| Математическое ожидание | [math]\displaystyle{ np }[/math] |
| Медиана | одно из [math]\displaystyle{ \{\lfloor np\rfloor-1, \lfloor np\rfloor, \lfloor np\rfloor+1\} }[/math] |
| Мода | [math]\displaystyle{ \lfloor (n+1)\,p\rfloor }[/math] |
| Дисперсия | [math]\displaystyle{ npq }[/math] |
| Коэффициент асимметрии | [math]\displaystyle{ \frac{q-p}{\sqrt{npq}} }[/math] |
| Коэффициент эксцесса | [math]\displaystyle{ \frac{1-6pq}{npq} }[/math] |
| Дифференциальная энтропия | [math]\displaystyle{ \frac12 \log_2 \big( 2\pi e\, np(1-p) \big) + O \left( \frac{1}{n} \right) }[/math] |
| Производящая функция моментов | [math]\displaystyle{ (q + pe^t)^n }[/math] |
| Характеристическая функция | [math]\displaystyle{ (q + pe^{it})^n }[/math] |
Биномиа́льное распределе́ние с параметрами [math]\displaystyle{ n }[/math] и [math]\displaystyle{ p }[/math] в теории вероятностей — распределение количества «успехов» в последовательности из [math]\displaystyle{ n }[/math] независимых случайных экспериментов по схеме Бернулли, таких, что вероятность «успеха» в каждом из них постоянна и равна [math]\displaystyle{ p }[/math].
Определение
Пусть [math]\displaystyle{ X_1 ,\ldots, X_n }[/math] — конечная последовательность независимых случайных величин, имеющих одинаковое распределение Бернулли с параметром [math]\displaystyle{ p }[/math], то есть при каждом [math]\displaystyle{ i=1,\ldots, n }[/math] величина [math]\displaystyle{ X_i }[/math] принимает значения [math]\displaystyle{ 1 }[/math] («успех») и [math]\displaystyle{ 0 }[/math] («неудача») с вероятностями [math]\displaystyle{ p }[/math] и [math]\displaystyle{ q=1-p }[/math] соответственно. Тогда случайная величина
- [math]\displaystyle{ Y = X_1+X_2+ \ldots +X_n }[/math]
имеет биномиальное распределение с параметрами [math]\displaystyle{ n }[/math] и [math]\displaystyle{ p }[/math]. Это записывается в виде:
- [math]\displaystyle{ Y \sim \mathrm{Bin}(n,p) }[/math].
Случайную величину [math]\displaystyle{ Y }[/math] обычно интерпретируют как число успехов в серии из [math]\displaystyle{ n }[/math] одинаковых независимых испытаний Бернулли с вероятностью успеха [math]\displaystyle{ p }[/math] в каждом испытании.
Функция вероятности задаётся формулой:
- [math]\displaystyle{ p_Y(k) \equiv \mathbb{P}(Y = k) = \binom{n}{k}\, p^k q^{n-k}, \ \ k=0,\ldots, n, }[/math]
где
- [math]\displaystyle{ \binom{n}{k} = C_n^k = \frac{n!}{(n-k)! \, k!} }[/math] — биномиальный коэффициент.
Термин "биномиальный" используется так как [math]\displaystyle{ C_n^k = \binom{n}{k}\, p^k q^{n-k} }[/math] представляет собой [math]\displaystyle{ k }[/math]-й член биномиального разложения [math]\displaystyle{ (p+k)^n }[/math].
Функция распределения
Функция распределения биномиального распределения может быть записана в виде суммы:
- [math]\displaystyle{ F_Y(y) \equiv \mathbb{P}(Y \leqslant y) = \sum\limits_{k=0}^{\lfloor y \rfloor} \binom{n}{k}\, p^k q^{n-k},\; y \in\mathbb{R} }[/math],
где [math]\displaystyle{ \lfloor y \rfloor }[/math] обозначает наибольшее целое, не превосходящее число [math]\displaystyle{ y }[/math], или в виде неполной бета-функции:
- [math]\displaystyle{ F_Y(y) \equiv \mathbb{P}(Y \leqslant y ) = I_{1-p}(n-\lfloor y \rfloor,\lfloor y \rfloor +1) }[/math].
Максимальная вероятность в биномиальном распределении
Если в формуле [math]\displaystyle{ C_n^k = \binom{n}{k}\, p^k q^{n-k} }[/math] [math]\displaystyle{ k }[/math] изменяется от 0 до [math]\displaystyle{ n }[/math], то вероятность [math]\displaystyle{ C_n^k }[/math] сначала монотонно возрастает, а затем монотонно убывает, достигая своего наибольшего значения при [math]\displaystyle{ m=(n+1)p }[/math], за исключением случаев когда [math]\displaystyle{ C_n^{m-1}=C_n^m }[/math]. [math]\displaystyle{ C_n^m }[/math] - максимальная вероятность или наиболее вероятное число успехов. Однако, при большом количестве испытаний, то есть при большом [math]\displaystyle{ n }[/math], максимальная вероятность будет небольшой.
Моменты
Производящая функция моментов биномиального распределения имеет вид:
- [math]\displaystyle{ M_Y(t) = \left( pe^t + q\right)^n }[/math], где [math]\displaystyle{ q = (1 - p) }[/math]
откуда
- [math]\displaystyle{ \mathbb{E}[Y] = np }[/math],
- [math]\displaystyle{ \mathbb{E}\left[Y^2\right] = np ( q + np ) }[/math],
а дисперсия случайной величины.
- [math]\displaystyle{ \mathbb{D}[Y] = npq }[/math].

Свойства биномиального распределения
- Пусть [math]\displaystyle{ Y_1 \sim \mathrm{Bin}(n,p) }[/math] и [math]\displaystyle{ Y_2 \sim \mathrm{Bin}(n, 1-p) }[/math]. Тогда [math]\displaystyle{ p_{Y_1}(k) = p_{Y_2}(n-k) }[/math].
- Пусть [math]\displaystyle{ Y_1 \sim \mathrm{Bin}(n_1,p) }[/math] и [math]\displaystyle{ Y_2 \sim \mathrm{Bin}(n_2,p) }[/math]. Тогда [math]\displaystyle{ Y_1 + Y_2 \sim \mathrm{Bin}(n_1+n_2, p) }[/math].
Связь с другими распределениями
- Если [math]\displaystyle{ n=1 }[/math], то получаем распределение Бернулли.
- Если [math]\displaystyle{ n }[/math] большое, то в силу центральной предельной теоремы [math]\displaystyle{ \mathrm{Bin}(n,p) \approx N( np, npq ) }[/math], где [math]\displaystyle{ N(np,npq) }[/math] — нормальное распределение с математическим ожиданием [math]\displaystyle{ np }[/math] и дисперсией [math]\displaystyle{ npq }[/math].
- Если [math]\displaystyle{ n }[/math] большое, [math]\displaystyle{ p }[/math] - малое, а [math]\displaystyle{ \lambda = np }[/math] — фиксированное число меньшее [math]\displaystyle{ 7 }[/math], то [math]\displaystyle{ \mathrm{Bin}(n, \lambda / n) \approx \mathrm{P}(\lambda) }[/math], где [math]\displaystyle{ \mathrm{P}(\lambda) }[/math] — распределение Пуассона с параметром [math]\displaystyle{ \lambda }[/math].
- Если случайные величины [math]\displaystyle{ X }[/math] и [math]\displaystyle{ Y }[/math] имеют биномиальные распределения [math]\displaystyle{ \mathrm{Bin}(D,p) }[/math] и [math]\displaystyle{ \mathrm{Bin}(N-D,p) }[/math] соответственно, то условное распределение случайной величины [math]\displaystyle{ X }[/math] при условии [math]\displaystyle{ X+Y=n }[/math] — гипергеометрическое [math]\displaystyle{ \mathrm{HG}(D,N,n) }[/math].
Таблицы функции распределения [math]\displaystyle{ \mathbb{P}(Y \leqslant y) }[/math] для вероятности биномиального распределения
При вычислении функции распределения для вероятности биномиального распределения применяются таблицы биномиального распределения. Например для [math]\displaystyle{ n=3 }[/math] независимых случайных экспериментов, функция распределения [math]\displaystyle{ F_Y(y) \equiv \mathbb{P}(Y \leqslant y) }[/math], или то, что число успехов будет не меньше [math]\displaystyle{ y }[/math], определяется по таблице (при различных значениях вероятности [math]\displaystyle{ p }[/math] в одном случайном эксперименте):
| [math]\displaystyle{ y }[/math] | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 | 0.55 | 0.6 | 0.65 | 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.857 | 0.729 | 0.614 | 0.512 | 0.422 | 0.343 | 0.275 | 0.216 | 0.166 | 0.125 | 0.091 | 0.064 | 0.043 | 0.027 | 0.016 | 0.008 | 0.003 | 0.001 | 0.000 |
| 1 | 0.993 | 0.972 | 0.939 | 0.896 | 0.844 | 0.784 | 0.718 | 0.648 | 0.575 | 0.500 | 0.425 | 0.352 | 0.282 | 0.216 | 0.156 | 0.104 | 0.061 | 0.028 | 0.007 |
| 2 | 1.000 | 0.999 | 0.997 | 0.992 | 0.984 | 0.973 | 0.957 | 0.936 | 0.909 | 0.875 | 0.834 | 0.784 | 0.725 | 0.657 | 0.578 | 0.488 | 0.386 | 0.271 | 0.143 |
| 3 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
Используя таблицы, можно найти вероятность того, что в [math]\displaystyle{ n=3 }[/math] независимых испытаниях событие наступит ровно [math]\displaystyle{ у }[/math] раз. Например, если вероятность наступления одного события равна [math]\displaystyle{ p=0,35 }[/math], то вероятность наступления двух событий в [math]\displaystyle{ n=3 }[/math] независимых испытаниях будет равна, согласно таблице:
- [math]\displaystyle{ P(X=2)=P(X \leqslant 2)-P(X \leqslant 1)=0,957-0,718=0,239 }[/math]
Таблица для числа независимых случайных экспериментов [math]\displaystyle{ n }[/math] от 2 до 50
| [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | [math]\displaystyle{ p }[/math] | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [math]\displaystyle{ n }[/math] | [math]\displaystyle{ y }[/math] | 0,01 | 0,05 | 0,1 | 0,15 | 0,2 | 0,25 | 0,3 | 0,35 | 0,4 | 0,45 | 0,5 | 0,55 | 0,6 | 0,65 | 0,7 | 0,75 | 0,8 | 0,85 | 0,9 | 0,95 |
| 2 | 0 | 0,980 | 0,903 | 0,810 | 0,723 | 0,640 | 0,563 | 0,490 | 0,423 | 0,360 | 0,303 | 0,250 | 0,203 | 0,160 | 0,123 | 0,090 | 0,063 | 0,040 | 0,023 | 0,010 | 0,003 |
| 1 | 1,000 | 0,998 | 0,990 | 0,978 | 0,960 | 0,938 | 0,910 | 0,878 | 0,840 | 0,798 | 0,750 | 0,698 | 0,640 | 0,578 | 0,510 | 0,438 | 0,360 | 0,278 | 0,190 | 0,098 | |
| 2 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 3 | 0 | 0,970 | 0,857 | 0,729 | 0,614 | 0,512 | 0,422 | 0,343 | 0,275 | 0,216 | 0,166 | 0,125 | 0,091 | 0,064 | 0,043 | 0,027 | 0,016 | 0,008 | 0,003 | 0,001 | 0,000 |
| 1 | 1,000 | 0,993 | 0,972 | 0,939 | 0,896 | 0,844 | 0,784 | 0,718 | 0,648 | 0,575 | 0,500 | 0,425 | 0,352 | 0,282 | 0,216 | 0,156 | 0,104 | 0,061 | 0,028 | 0,007 | |
| 2 | 1,000 | 1,000 | 0,999 | 0,997 | 0,992 | 0,984 | 0,973 | 0,957 | 0,936 | 0,909 | 0,875 | 0,834 | 0,784 | 0,725 | 0,657 | 0,578 | 0,488 | 0,386 | 0,271 | 0,143 | |
| 3 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 4 | 0 | 0,961 | 0,815 | 0,656 | 0,522 | 0,410 | 0,316 | 0,240 | 0,179 | 0,130 | 0,092 | 0,063 | 0,041 | 0,026 | 0,015 | 0,008 | 0,004 | 0,002 | 0,001 | 0,000 | 0,000 |
| 1 | 0,999 | 0,986 | 0,948 | 0,890 | 0,819 | 0,738 | 0,652 | 0,563 | 0,475 | 0,391 | 0,313 | 0,241 | 0,179 | 0,126 | 0,084 | 0,051 | 0,027 | 0,012 | 0,004 | 0,000 | |
| 2 | 1,000 | 1,000 | 0,996 | 0,988 | 0,973 | 0,949 | 0,916 | 0,874 | 0,821 | 0,759 | 0,688 | 0,609 | 0,525 | 0,437 | 0,348 | 0,262 | 0,181 | 0,110 | 0,052 | 0,014 | |
| 3 | 1,000 | 1,000 | 1,000 | 0,999 | 0,998 | 0,996 | 0,992 | 0,985 | 0,974 | 0,959 | 0,938 | 0,908 | 0,870 | 0,821 | 0,760 | 0,684 | 0,590 | 0,478 | 0,344 | 0,185 | |
| 4 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 5 | 0 | 0,951 | 0,774 | 0,590 | 0,444 | 0,328 | 0,237 | 0,168 | 0,116 | 0,078 | 0,050 | 0,031 | 0,018 | 0,010 | 0,005 | 0,002 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,999 | 0,977 | 0,919 | 0,835 | 0,737 | 0,633 | 0,528 | 0,428 | 0,337 | 0,256 | 0,188 | 0,131 | 0,087 | 0,054 | 0,031 | 0,016 | 0,007 | 0,002 | 0,000 | 0,000 | |
| 2 | 1,000 | 0,999 | 0,991 | 0,973 | 0,942 | 0,896 | 0,837 | 0,765 | 0,683 | 0,593 | 0,500 | 0,407 | 0,317 | 0,235 | 0,163 | 0,104 | 0,058 | 0,027 | 0,009 | 0,001 | |
| 3 | 1,000 | 1,000 | 1,000 | 0,998 | 0,993 | 0,984 | 0,969 | 0,946 | 0,913 | 0,869 | 0,813 | 0,744 | 0,663 | 0,572 | 0,472 | 0,367 | 0,263 | 0,165 | 0,081 | 0,023 | |
| 4 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,998 | 0,995 | 0,990 | 0,982 | 0,969 | 0,950 | 0,922 | 0,884 | 0,832 | 0,763 | 0,672 | 0,556 | 0,410 | 0,226 | |
| 5 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 6 | 0 | 0,941 | 0,735 | 0,531 | 0,377 | 0,262 | 0,178 | 0,118 | 0,075 | 0,047 | 0,028 | 0,016 | 0,008 | 0,004 | 0,002 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,999 | 0,967 | 0,886 | 0,776 | 0,655 | 0,534 | 0,420 | 0,319 | 0,233 | 0,164 | 0,109 | 0,069 | 0,041 | 0,022 | 0,011 | 0,005 | 0,002 | 0,000 | 0,000 | 0,000 | |
| 2 | 1,000 | 0,998 | 0,984 | 0,953 | 0,901 | 0,831 | 0,744 | 0,647 | 0,544 | 0,442 | 0,344 | 0,255 | 0,179 | 0,117 | 0,070 | 0,038 | 0,017 | 0,006 | 0,001 | 0,000 | |
| 3 | 1,000 | 1,000 | 0,999 | 0,994 | 0,983 | 0,962 | 0,930 | 0,883 | 0,821 | 0,745 | 0,656 | 0,558 | 0,456 | 0,353 | 0,256 | 0,169 | 0,099 | 0,047 | 0,016 | 0,002 | |
| 4 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,995 | 0,989 | 0,978 | 0,959 | 0,931 | 0,891 | 0,836 | 0,767 | 0,681 | 0,580 | 0,466 | 0,345 | 0,224 | 0,114 | 0,033 | |
| 5 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,998 | 0,996 | 0,992 | 0,984 | 0,972 | 0,953 | 0,925 | 0,882 | 0,822 | 0,738 | 0,623 | 0,469 | 0,265 | |
| 6 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 7 | 0 | 0,932 | 0,698 | 0,478 | 0,321 | 0,210 | 0,133 | 0,082 | 0,049 | 0,028 | 0,015 | 0,008 | 0,004 | 0,002 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,998 | 0,956 | 0,850 | 0,717 | 0,577 | 0,445 | 0,329 | 0,234 | 0,159 | 0,102 | 0,063 | 0,036 | 0,019 | 0,009 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 2 | 1,000 | 0,996 | 0,974 | 0,926 | 0,852 | 0,756 | 0,647 | 0,532 | 0,420 | 0,316 | 0,227 | 0,153 | 0,096 | 0,056 | 0,029 | 0,013 | 0,005 | 0,001 | 0,000 | 0,000 | |
| 3 | 1,000 | 1,000 | 0,997 | 0,988 | 0,967 | 0,929 | 0,874 | 0,800 | 0,710 | 0,608 | 0,500 | 0,392 | 0,290 | 0,200 | 0,126 | 0,071 | 0,033 | 0,012 | 0,003 | 0,000 | |
| 4 | 1,000 | 1,000 | 1,000 | 0,999 | 0,995 | 0,987 | 0,971 | 0,944 | 0,904 | 0,847 | 0,773 | 0,684 | 0,580 | 0,468 | 0,353 | 0,244 | 0,148 | 0,074 | 0,026 | 0,004 | |
| 5 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,991 | 0,981 | 0,964 | 0,938 | 0,898 | 0,841 | 0,766 | 0,671 | 0,555 | 0,423 | 0,283 | 0,150 | 0,044 | |
| 6 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,998 | 0,996 | 0,992 | 0,985 | 0,972 | 0,951 | 0,918 | 0,867 | 0,790 | 0,679 | 0,522 | 0,302 | |
| 7 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 8 | 0 | 0,923 | 0,663 | 0,430 | 0,272 | 0,168 | 0,100 | 0,058 | 0,032 | 0,017 | 0,008 | 0,004 | 0,002 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,997 | 0,943 | 0,813 | 0,657 | 0,503 | 0,367 | 0,255 | 0,169 | 0,106 | 0,063 | 0,035 | 0,018 | 0,009 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 2 | 1,000 | 0,994 | 0,962 | 0,895 | 0,797 | 0,679 | 0,552 | 0,428 | 0,315 | 0,220 | 0,145 | 0,088 | 0,050 | 0,025 | 0,011 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | |
| 3 | 1,000 | 1,000 | 0,995 | 0,979 | 0,944 | 0,886 | 0,806 | 0,706 | 0,594 | 0,477 | 0,363 | 0,260 | 0,174 | 0,106 | 0,058 | 0,027 | 0,010 | 0,003 | 0,000 | 0,000 | |
| 4 | 1,000 | 1,000 | 1,000 | 0,997 | 0,990 | 0,973 | 0,942 | 0,894 | 0,826 | 0,740 | 0,637 | 0,523 | 0,406 | 0,294 | 0,194 | 0,114 | 0,056 | 0,021 | 0,005 | 0,000 | |
| 5 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,989 | 0,975 | 0,950 | 0,912 | 0,855 | 0,780 | 0,685 | 0,572 | 0,448 | 0,321 | 0,203 | 0,105 | 0,038 | 0,006 | |
| 6 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,991 | 0,982 | 0,965 | 0,937 | 0,894 | 0,831 | 0,745 | 0,633 | 0,497 | 0,343 | 0,187 | 0,057 | |
| 7 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,998 | 0,996 | 0,992 | 0,983 | 0,968 | 0,942 | 0,900 | 0,832 | 0,728 | 0,570 | 0,337 | |
| 8 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 9 | 0 | 0,914 | 0,630 | 0,387 | 0,232 | 0,134 | 0,075 | 0,040 | 0,021 | 0,010 | 0,005 | 0,002 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,997 | 0,929 | 0,775 | 0,599 | 0,436 | 0,300 | 0,196 | 0,121 | 0,071 | 0,039 | 0,020 | 0,009 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 2 | 1,000 | 0,992 | 0,947 | 0,859 | 0,738 | 0,601 | 0,463 | 0,337 | 0,232 | 0,150 | 0,090 | 0,050 | 0,025 | 0,011 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 3 | 1,000 | 0,999 | 0,992 | 0,966 | 0,914 | 0,834 | 0,730 | 0,609 | 0,483 | 0,361 | 0,254 | 0,166 | 0,099 | 0,054 | 0,025 | 0,010 | 0,003 | 0,001 | 0,000 | 0,000 | |
| 4 | 1,000 | 1,000 | 0,999 | 0,994 | 0,980 | 0,951 | 0,901 | 0,828 | 0,733 | 0,621 | 0,500 | 0,379 | 0,267 | 0,172 | 0,099 | 0,049 | 0,020 | 0,006 | 0,001 | 0,000 | |
| 5 | 1,000 | 1,000 | 1,000 | 0,999 | 0,997 | 0,990 | 0,975 | 0,946 | 0,901 | 0,834 | 0,746 | 0,639 | 0,517 | 0,391 | 0,270 | 0,166 | 0,086 | 0,034 | 0,008 | 0,001 | |
| 6 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,989 | 0,975 | 0,950 | 0,910 | 0,850 | 0,768 | 0,663 | 0,537 | 0,399 | 0,262 | 0,141 | 0,053 | 0,008 | |
| 7 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,991 | 0,980 | 0,961 | 0,929 | 0,879 | 0,804 | 0,700 | 0,564 | 0,401 | 0,225 | 0,071 | |
| 8 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,998 | 0,995 | 0,990 | 0,979 | 0,960 | 0,925 | 0,866 | 0,768 | 0,613 | 0,370 | |
| 9 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 10 | 0 | 0,904 | 0,599 | 0,349 | 0,197 | 0,107 | 0,056 | 0,028 | 0,013 | 0,006 | 0,003 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,996 | 0,914 | 0,736 | 0,544 | 0,376 | 0,244 | 0,149 | 0,086 | 0,046 | 0,023 | 0,011 | 0,005 | 0,002 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 2 | 1,000 | 0,988 | 0,930 | 0,820 | 0,678 | 0,526 | 0,383 | 0,262 | 0,167 | 0,100 | 0,055 | 0,027 | 0,012 | 0,005 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 3 | 1,000 | 0,999 | 0,987 | 0,950 | 0,879 | 0,776 | 0,650 | 0,514 | 0,382 | 0,266 | 0,172 | 0,102 | 0,055 | 0,026 | 0,011 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | |
| 4 | 1,000 | 1,000 | 0,998 | 0,990 | 0,967 | 0,922 | 0,850 | 0,751 | 0,633 | 0,504 | 0,377 | 0,262 | 0,166 | 0,095 | 0,047 | 0,020 | 0,006 | 0,001 | 0,000 | 0,000 | |
| 5 | 1,000 | 1,000 | 1,000 | 0,999 | 0,994 | 0,980 | 0,953 | 0,905 | 0,834 | 0,738 | 0,623 | 0,496 | 0,367 | 0,249 | 0,150 | 0,078 | 0,033 | 0,010 | 0,002 | 0,000 | |
| 6 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,989 | 0,974 | 0,945 | 0,898 | 0,828 | 0,734 | 0,618 | 0,486 | 0,350 | 0,224 | 0,121 | 0,050 | 0,013 | 0,001 | |
| 7 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,995 | 0,988 | 0,973 | 0,945 | 0,900 | 0,833 | 0,738 | 0,617 | 0,474 | 0,322 | 0,180 | 0,070 | 0,012 | |
| 8 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,998 | 0,995 | 0,989 | 0,977 | 0,954 | 0,914 | 0,851 | 0,756 | 0,624 | 0,456 | 0,264 | 0,086 | |
| 9 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,997 | 0,994 | 0,987 | 0,972 | 0,944 | 0,893 | 0,803 | 0,651 | 0,401 | |
| 10 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 15 | 0 | 0,860 | 0,463 | 0,206 | 0,087 | 0,035 | 0,013 | 0,005 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,990 | 0,829 | 0,549 | 0,319 | 0,167 | 0,080 | 0,035 | 0,014 | 0,005 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 2 | 1,000 | 0,964 | 0,816 | 0,604 | 0,398 | 0,236 | 0,127 | 0,062 | 0,027 | 0,011 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 3 | 1,000 | 0,995 | 0,944 | 0,823 | 0,648 | 0,461 | 0,297 | 0,173 | 0,091 | 0,042 | 0,018 | 0,006 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 4 | 1,000 | 0,999 | 0,987 | 0,938 | 0,836 | 0,686 | 0,515 | 0,352 | 0,217 | 0,120 | 0,059 | 0,025 | 0,009 | 0,003 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 5 | 1,000 | 1,000 | 0,998 | 0,983 | 0,939 | 0,852 | 0,722 | 0,564 | 0,403 | 0,261 | 0,151 | 0,077 | 0,034 | 0,012 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 6 | 1,000 | 1,000 | 1,000 | 0,996 | 0,982 | 0,943 | 0,869 | 0,755 | 0,610 | 0,452 | 0,304 | 0,182 | 0,095 | 0,042 | 0,015 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | |
| 7 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,983 | 0,950 | 0,887 | 0,787 | 0,654 | 0,500 | 0,346 | 0,213 | 0,113 | 0,050 | 0,017 | 0,004 | 0,001 | 0,000 | 0,000 | |
| 8 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,985 | 0,958 | 0,905 | 0,818 | 0,696 | 0,548 | 0,390 | 0,245 | 0,131 | 0,057 | 0,018 | 0,004 | 0,000 | 0,000 | |
| 9 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,988 | 0,966 | 0,923 | 0,849 | 0,739 | 0,597 | 0,436 | 0,278 | 0,148 | 0,061 | 0,017 | 0,002 | 0,000 | |
| 10 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,997 | 0,991 | 0,975 | 0,941 | 0,880 | 0,783 | 0,648 | 0,485 | 0,314 | 0,164 | 0,062 | 0,013 | 0,001 | |
| 11 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,994 | 0,982 | 0,958 | 0,909 | 0,827 | 0,703 | 0,539 | 0,352 | 0,177 | 0,056 | 0,005 | |
| 12 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,989 | 0,973 | 0,938 | 0,873 | 0,764 | 0,602 | 0,396 | 0,184 | 0,036 | |
| 13 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,995 | 0,986 | 0,965 | 0,920 | 0,833 | 0,681 | 0,451 | 0,171 | |
| 14 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,995 | 0,987 | 0,965 | 0,913 | 0,794 | 0,537 | |
| 15 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 20 | 0 | 0,818 | 0,358 | 0,122 | 0,039 | 0,012 | 0,003 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,983 | 0,736 | 0,392 | 0,176 | 0,069 | 0,024 | 0,008 | 0,002 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 2 | 0,999 | 0,925 | 0,677 | 0,405 | 0,206 | 0,091 | 0,035 | 0,012 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 3 | 1,000 | 0,984 | 0,867 | 0,648 | 0,411 | 0,225 | 0,107 | 0,044 | 0,016 | 0,005 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 4 | 1,000 | 0,997 | 0,957 | 0,830 | 0,630 | 0,415 | 0,238 | 0,118 | 0,051 | 0,019 | 0,006 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 5 | 1,000 | 1,000 | 0,989 | 0,933 | 0,804 | 0,617 | 0,416 | 0,245 | 0,126 | 0,055 | 0,021 | 0,006 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 6 | 1,000 | 1,000 | 0,998 | 0,978 | 0,913 | 0,786 | 0,608 | 0,417 | 0,250 | 0,130 | 0,058 | 0,021 | 0,006 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 7 | 1,000 | 1,000 | 1,000 | 0,994 | 0,968 | 0,898 | 0,772 | 0,601 | 0,416 | 0,252 | 0,132 | 0,058 | 0,021 | 0,006 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 8 | 1,000 | 1,000 | 1,000 | 0,999 | 0,990 | 0,959 | 0,887 | 0,762 | 0,596 | 0,414 | 0,252 | 0,131 | 0,057 | 0,020 | 0,005 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 9 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,986 | 0,952 | 0,878 | 0,755 | 0,591 | 0,412 | 0,249 | 0,128 | 0,053 | 0,017 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | |
| 10 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,983 | 0,947 | 0,872 | 0,751 | 0,588 | 0,409 | 0,245 | 0,122 | 0,048 | 0,014 | 0,003 | 0,000 | 0,000 | 0,000 | |
| 11 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,995 | 0,980 | 0,943 | 0,869 | 0,748 | 0,586 | 0,404 | 0,238 | 0,113 | 0,041 | 0,010 | 0,001 | 0,000 | 0,000 | |
| 12 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,994 | 0,979 | 0,942 | 0,868 | 0,748 | 0,584 | 0,399 | 0,228 | 0,102 | 0,032 | 0,006 | 0,000 | 0,000 | |
| 13 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,994 | 0,979 | 0,942 | 0,870 | 0,750 | 0,583 | 0,392 | 0,214 | 0,087 | 0,022 | 0,002 | 0,000 | |
| 14 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,994 | 0,979 | 0,945 | 0,874 | 0,755 | 0,584 | 0,383 | 0,196 | 0,067 | 0,011 | 0,000 | |
| 15 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,994 | 0,981 | 0,949 | 0,882 | 0,762 | 0,585 | 0,370 | 0,170 | 0,043 | 0,003 | |
| 16 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,995 | 0,984 | 0,956 | 0,893 | 0,775 | 0,589 | 0,352 | 0,133 | 0,016 | |
| 17 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,988 | 0,965 | 0,909 | 0,794 | 0,595 | 0,323 | 0,075 | |
| 18 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,998 | 0,992 | 0,976 | 0,931 | 0,824 | 0,608 | 0,264 | |
| 19 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,997 | 0,988 | 0,961 | 0,878 | 0,642 | |
| 20 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 30 | 0 | 0,740 | 0,215 | 0,042 | 0,008 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,964 | 0,554 | 0,184 | 0,048 | 0,011 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 2 | 0,997 | 0,812 | 0,411 | 0,151 | 0,044 | 0,011 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 3 | 1,000 | 0,939 | 0,647 | 0,322 | 0,123 | 0,037 | 0,009 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 4 | 1,000 | 0,984 | 0,825 | 0,524 | 0,255 | 0,098 | 0,030 | 0,008 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 5 | 1,000 | 0,997 | 0,927 | 0,711 | 0,428 | 0,203 | 0,077 | 0,023 | 0,006 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 6 | 1,000 | 0,999 | 0,974 | 0,847 | 0,607 | 0,348 | 0,160 | 0,059 | 0,017 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 7 | 1,000 | 1,000 | 0,992 | 0,930 | 0,761 | 0,514 | 0,281 | 0,124 | 0,044 | 0,012 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 8 | 1,000 | 1,000 | 0,998 | 0,972 | 0,871 | 0,674 | 0,432 | 0,225 | 0,094 | 0,031 | 0,008 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 9 | 1,000 | 1,000 | 1,000 | 0,990 | 0,939 | 0,803 | 0,589 | 0,358 | 0,176 | 0,069 | 0,021 | 0,005 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 10 | 1,000 | 1,000 | 1,000 | 0,997 | 0,974 | 0,894 | 0,730 | 0,508 | 0,291 | 0,135 | 0,049 | 0,014 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 11 | 1,000 | 1,000 | 1,000 | 0,999 | 0,991 | 0,949 | 0,841 | 0,655 | 0,431 | 0,233 | 0,100 | 0,033 | 0,008 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 12 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,978 | 0,916 | 0,780 | 0,578 | 0,359 | 0,181 | 0,071 | 0,021 | 0,005 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 13 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,992 | 0,960 | 0,874 | 0,715 | 0,502 | 0,292 | 0,136 | 0,048 | 0,012 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 14 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,983 | 0,935 | 0,825 | 0,645 | 0,428 | 0,231 | 0,097 | 0,030 | 0,006 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 15 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,994 | 0,970 | 0,903 | 0,769 | 0,572 | 0,355 | 0,175 | 0,065 | 0,017 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 16 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,988 | 0,952 | 0,864 | 0,708 | 0,498 | 0,285 | 0,126 | 0,040 | 0,008 | 0,001 | 0,000 | 0,000 | 0,000 | |
| 17 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,995 | 0,979 | 0,929 | 0,819 | 0,641 | 0,422 | 0,220 | 0,084 | 0,022 | 0,003 | 0,000 | 0,000 | 0,000 | |
| 18 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,992 | 0,967 | 0,900 | 0,767 | 0,569 | 0,345 | 0,159 | 0,051 | 0,009 | 0,001 | 0,000 | 0,000 | |
| 19 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,986 | 0,951 | 0,865 | 0,709 | 0,492 | 0,270 | 0,106 | 0,026 | 0,003 | 0,000 | 0,000 | |
| 20 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,995 | 0,979 | 0,931 | 0,824 | 0,642 | 0,411 | 0,197 | 0,061 | 0,010 | 0,000 | 0,000 | |
| 21 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,992 | 0,969 | 0,906 | 0,775 | 0,568 | 0,326 | 0,129 | 0,028 | 0,002 | 0,000 | |
| 22 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,988 | 0,956 | 0,876 | 0,719 | 0,486 | 0,239 | 0,070 | 0,008 | 0,000 | |
| 23 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,983 | 0,941 | 0,840 | 0,652 | 0,393 | 0,153 | 0,026 | 0,001 | |
| 24 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,994 | 0,977 | 0,923 | 0,797 | 0,572 | 0,289 | 0,073 | 0,003 | |
| 25 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,992 | 0,970 | 0,902 | 0,745 | 0,476 | 0,175 | 0,016 | |
| 26 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,991 | 0,963 | 0,877 | 0,678 | 0,353 | 0,061 | |
| 27 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,989 | 0,956 | 0,849 | 0,589 | 0,188 | |
| 28 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,989 | 0,952 | 0,816 | 0,446 | |
| 29 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,992 | 0,958 | 0,785 | |
| 30 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 40 | 0 | 0,669 | 0,129 | 0,015 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,939 | 0,399 | 0,080 | 0,012 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 2 | 0,993 | 0,677 | 0,223 | 0,049 | 0,008 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 3 | 0,999 | 0,862 | 0,423 | 0,130 | 0,028 | 0,005 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 4 | 1,000 | 0,952 | 0,629 | 0,263 | 0,076 | 0,016 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 5 | 1,000 | 0,986 | 0,794 | 0,433 | 0,161 | 0,043 | 0,009 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 6 | 1,000 | 0,997 | 0,900 | 0,607 | 0,286 | 0,096 | 0,024 | 0,004 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 7 | 1,000 | 0,999 | 0,958 | 0,756 | 0,437 | 0,182 | 0,055 | 0,012 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 8 | 1,000 | 1,000 | 0,985 | 0,865 | 0,593 | 0,300 | 0,111 | 0,030 | 0,006 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 9 | 1,000 | 1,000 | 0,995 | 0,933 | 0,732 | 0,440 | 0,196 | 0,064 | 0,016 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 10 | 1,000 | 1,000 | 0,999 | 0,970 | 0,839 | 0,584 | 0,309 | 0,121 | 0,035 | 0,007 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 11 | 1,000 | 1,000 | 1,000 | 0,988 | 0,912 | 0,715 | 0,441 | 0,205 | 0,071 | 0,018 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 12 | 1,000 | 1,000 | 1,000 | 0,996 | 0,957 | 0,821 | 0,577 | 0,314 | 0,129 | 0,039 | 0,008 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 13 | 1,000 | 1,000 | 1,000 | 0,999 | 0,981 | 0,897 | 0,703 | 0,441 | 0,211 | 0,075 | 0,019 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 14 | 1,000 | 1,000 | 1,000 | 1,000 | 0,992 | 0,946 | 0,807 | 0,572 | 0,317 | 0,133 | 0,040 | 0,009 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 15 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,974 | 0,885 | 0,695 | 0,440 | 0,214 | 0,077 | 0,020 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 16 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,988 | 0,937 | 0,798 | 0,568 | 0,319 | 0,134 | 0,041 | 0,008 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 17 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,995 | 0,968 | 0,876 | 0,689 | 0,439 | 0,215 | 0,077 | 0,019 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 18 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,985 | 0,930 | 0,791 | 0,565 | 0,318 | 0,133 | 0,039 | 0,008 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 19 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,994 | 0,964 | 0,870 | 0,684 | 0,437 | 0,213 | 0,074 | 0,017 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 20 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,983 | 0,926 | 0,787 | 0,563 | 0,316 | 0,130 | 0,036 | 0,006 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 21 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,992 | 0,961 | 0,867 | 0,682 | 0,435 | 0,209 | 0,070 | 0,015 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 22 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,981 | 0,923 | 0,785 | 0,561 | 0,311 | 0,124 | 0,032 | 0,005 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 23 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,992 | 0,959 | 0,866 | 0,681 | 0,432 | 0,202 | 0,063 | 0,012 | 0,001 | 0,000 | 0,000 | 0,000 | |
| 24 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,980 | 0,923 | 0,786 | 0,560 | 0,305 | 0,115 | 0,026 | 0,003 | 0,000 | 0,000 | 0,000 | |
| 25 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,991 | 0,960 | 0,867 | 0,683 | 0,428 | 0,193 | 0,054 | 0,008 | 0,000 | 0,000 | 0,000 | |
| 26 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,981 | 0,925 | 0,789 | 0,559 | 0,297 | 0,103 | 0,019 | 0,001 | 0,000 | 0,000 | |
| 27 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,992 | 0,961 | 0,871 | 0,686 | 0,423 | 0,179 | 0,043 | 0,004 | 0,000 | 0,000 | |
| 28 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,982 | 0,929 | 0,795 | 0,559 | 0,285 | 0,088 | 0,012 | 0,000 | 0,000 | |
| 29 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,993 | 0,965 | 0,879 | 0,691 | 0,416 | 0,161 | 0,030 | 0,001 | 0,000 | |
| 30 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,984 | 0,936 | 0,804 | 0,560 | 0,268 | 0,067 | 0,005 | 0,000 | |
| 31 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,994 | 0,970 | 0,889 | 0,700 | 0,407 | 0,135 | 0,015 | 0,000 | |
| 32 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,988 | 0,945 | 0,818 | 0,563 | 0,244 | 0,042 | 0,001 | |
| 33 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,996 | 0,976 | 0,904 | 0,714 | 0,393 | 0,100 | 0,003 | |
| 34 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,991 | 0,957 | 0,839 | 0,567 | 0,206 | 0,014 | |
| 35 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,984 | 0,924 | 0,737 | 0,371 | 0,048 | |
| 36 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,995 | 0,972 | 0,870 | 0,577 | 0,138 | |
| 37 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,992 | 0,951 | 0,777 | 0,323 | |
| 38 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,988 | 0,920 | 0,601 | |
| 39 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,985 | 0,871 | |
| 40 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 50 | 0 | 0,605 | 0,077 | 0,005 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,911 | 0,279 | 0,034 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 2 | 0,986 | 0,541 | 0,112 | 0,014 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 3 | 0,998 | 0,760 | 0,250 | 0,046 | 0,006 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 4 | 1,000 | 0,896 | 0,431 | 0,112 | 0,018 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 5 | 1,000 | 0,962 | 0,616 | 0,219 | 0,048 | 0,007 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 6 | 1,000 | 0,988 | 0,770 | 0,361 | 0,103 | 0,019 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 7 | 1,000 | 0,997 | 0,878 | 0,519 | 0,190 | 0,045 | 0,007 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 8 | 1,000 | 0,999 | 0,942 | 0,668 | 0,307 | 0,092 | 0,018 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 9 | 1,000 | 1,000 | 0,975 | 0,791 | 0,444 | 0,164 | 0,040 | 0,007 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 10 | 1,000 | 1,000 | 0,991 | 0,880 | 0,584 | 0,262 | 0,079 | 0,016 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 11 | 1,000 | 1,000 | 0,997 | 0,937 | 0,711 | 0,382 | 0,139 | 0,034 | 0,006 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 12 | 1,000 | 1,000 | 0,999 | 0,970 | 0,814 | 0,511 | 0,223 | 0,066 | 0,013 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 13 | 1,000 | 1,000 | 1,000 | 0,987 | 0,889 | 0,637 | 0,328 | 0,116 | 0,028 | 0,004 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 14 | 1,000 | 1,000 | 1,000 | 0,995 | 0,939 | 0,748 | 0,447 | 0,188 | 0,054 | 0,010 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 15 | 1,000 | 1,000 | 1,000 | 0,998 | 0,969 | 0,837 | 0,569 | 0,280 | 0,096 | 0,022 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 16 | 1,000 | 1,000 | 1,000 | 0,999 | 0,986 | 0,902 | 0,684 | 0,389 | 0,156 | 0,043 | 0,008 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 17 | 1,000 | 1,000 | 1,000 | 1,000 | 0,994 | 0,945 | 0,782 | 0,506 | 0,237 | 0,077 | 0,016 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 18 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,971 | 0,859 | 0,622 | 0,336 | 0,127 | 0,032 | 0,005 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 19 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,986 | 0,915 | 0,726 | 0,446 | 0,197 | 0,059 | 0,012 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 20 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,994 | 0,952 | 0,814 | 0,561 | 0,286 | 0,101 | 0,024 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 21 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,975 | 0,881 | 0,670 | 0,390 | 0,161 | 0,044 | 0,008 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 22 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,988 | 0,929 | 0,766 | 0,502 | 0,240 | 0,078 | 0,016 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 23 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,994 | 0,960 | 0,844 | 0,613 | 0,336 | 0,128 | 0,031 | 0,005 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 24 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,979 | 0,902 | 0,716 | 0,444 | 0,197 | 0,057 | 0,010 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 25 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,990 | 0,943 | 0,803 | 0,556 | 0,284 | 0,098 | 0,021 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 26 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,995 | 0,969 | 0,872 | 0,664 | 0,387 | 0,156 | 0,040 | 0,006 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 27 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,984 | 0,922 | 0,760 | 0,498 | 0,234 | 0,071 | 0,012 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 28 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,992 | 0,956 | 0,839 | 0,610 | 0,330 | 0,119 | 0,025 | 0,003 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 29 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,976 | 0,899 | 0,714 | 0,439 | 0,186 | 0,048 | 0,006 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 30 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,988 | 0,941 | 0,803 | 0,554 | 0,274 | 0,085 | 0,014 | 0,001 | 0,000 | 0,000 | 0,000 | |
| 31 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,995 | 0,968 | 0,873 | 0,664 | 0,378 | 0,141 | 0,029 | 0,003 | 0,000 | 0,000 | 0,000 | |
| 32 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,984 | 0,923 | 0,763 | 0,494 | 0,218 | 0,055 | 0,006 | 0,000 | 0,000 | 0,000 | |
| 33 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,992 | 0,957 | 0,844 | 0,611 | 0,316 | 0,098 | 0,014 | 0,001 | 0,000 | 0,000 | |
| 34 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,978 | 0,904 | 0,720 | 0,431 | 0,163 | 0,031 | 0,002 | 0,000 | 0,000 | |
| 35 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,990 | 0,946 | 0,812 | 0,553 | 0,252 | 0,061 | 0,005 | 0,000 | 0,000 | |
| 36 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,996 | 0,972 | 0,884 | 0,672 | 0,363 | 0,111 | 0,013 | 0,000 | 0,000 | |
| 37 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,987 | 0,934 | 0,777 | 0,489 | 0,186 | 0,030 | 0,001 | 0,000 | |
| 38 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,994 | 0,966 | 0,861 | 0,618 | 0,289 | 0,063 | 0,003 | 0,000 | |
| 39 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,984 | 0,921 | 0,738 | 0,416 | 0,120 | 0,009 | 0,000 | |
| 40 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,993 | 0,960 | 0,836 | 0,556 | 0,209 | 0,025 | 0,000 | |
| 41 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,982 | 0,908 | 0,693 | 0,332 | 0,058 | 0,001 | |
| 42 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,993 | 0,955 | 0,810 | 0,481 | 0,122 | 0,003 | |
| 43 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,981 | 0,897 | 0,639 | 0,230 | 0,012 | |
| 44 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,993 | 0,952 | 0,781 | 0,384 | 0,038 | |
| 45 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,998 | 0,982 | 0,888 | 0,569 | 0,104 | |
| 46 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,994 | 0,954 | 0,750 | 0,240 | |
| 47 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,999 | 0,986 | 0,888 | 0,459 | |
| 48 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,997 | 0,966 | 0,721 | |
| 49 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,995 | 0,923 | |
| 50 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
См. также
В статье не хватает ссылок на источники (см. также рекомендации по поиску). |