Распределение Фишера
Внешний вид
| Распределение Фишера (Распределение Снедекора) | |
|---|---|
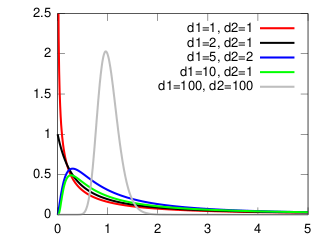 Плотность вероятности Плотность вероятности | |
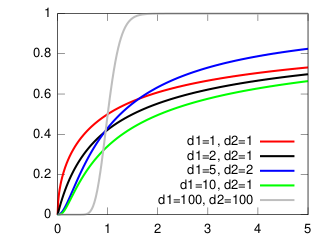 Функция распределения Функция распределения | |
| Обозначение | [math]\displaystyle{ F(d_1,d_2) }[/math] |
| Параметры | [math]\displaystyle{ d_1\gt 0,\ d_2\gt 0 }[/math] - числа степеней свободы |
| Носитель | [math]\displaystyle{ x \in [0; +\infty) }[/math] |
| Плотность вероятности | [math]\displaystyle{ \frac{\sqrt{\frac{(d_1\,x)^{d_1}\,\,d_2^{d_2}} {(d_1\,x+d_2)^{d_1+d_2}}}} {x\,\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)} }[/math] |
| Функция распределения | [math]\displaystyle{ I_{\frac{d_1 x}{d_1 x + d_2}}(d_1/2, d_2/2) }[/math] |
| Математическое ожидание | [math]\displaystyle{ \frac{d_2}{d_2-2} }[/math], если [math]\displaystyle{ d_2 \gt 2 }[/math] |
| Мода | [math]\displaystyle{ \frac{d_1-2}{d_1}\;\frac{d_2}{d_2+2} }[/math], если [math]\displaystyle{ d_1 \gt 2 }[/math] |
| Дисперсия | [math]\displaystyle{ \frac{2\,d_2^2\,(d_1+d_2-2)}{d_1 (d_2-2)^2 (d_2-4)}, }[/math] если [math]\displaystyle{ d_2 \gt 4 }[/math] |
| Коэффициент асимметрии |
[math]\displaystyle{ \frac{(2 d_1 + d_2 - 2) \sqrt{8 (d_2-4)}}{(d_2-6) \sqrt{d_1 (d_1 + d_2 -2)}}, }[/math] если [math]\displaystyle{ d_2 \gt 6 }[/math] |
| Производящая функция моментов | не существует[1] |
Распределе́ние Фи́шера в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений.
Определение
Пусть [math]\displaystyle{ Y_1,Y_2 }[/math] — две независимые случайные величины, имеющие распределение хи-квадрат: [math]\displaystyle{ Y_i \sim \chi^2(d_i) }[/math], где [math]\displaystyle{ d_i \in \mathbb{N},\; i=1,2 }[/math]. Тогда распределение случайной величины
- [math]\displaystyle{ F = \frac{Y_1/d_1}{Y_2/d_2} }[/math] называется распределением Фишера (распределением Снедекора) со степенями свободы [math]\displaystyle{ d_1 }[/math] и [math]\displaystyle{ d_2 }[/math]. Пишут [math]\displaystyle{ F \sim \mathrm{F}(d_1,d_2) }[/math].
Моменты
Математическое ожидание и дисперсия случайной величины, имеющей распределение Фишера, имеют вид:
- [math]\displaystyle{ \mathbb{M}[F] = \frac{d_2}{d_2 - 2} }[/math], если [math]\displaystyle{ d_2 \gt 2 }[/math],
- [math]\displaystyle{ \mathrm{D}[F] = \frac{2\,d_2^2\,(d_1+d_2-2)}{d_1 (d_2-2)^2 (d_2-4)} }[/math], если [math]\displaystyle{ d_2 \gt 4 }[/math].
Свойства распределения Фишера
- Если [math]\displaystyle{ F \sim \mathrm{F}(d_1,d_2) }[/math], то [math]\displaystyle{ \frac{1}{F} \sim \mathrm{F}(d_2, d_1) }[/math].
- Распределение Фишера сходится к единице. Доказательство:
если [math]\displaystyle{ F_{d_1,d_2} \sim \mathrm{F}(d_1,d_2) }[/math], то [math]\displaystyle{ F_{d_1,d_2} \to \delta(x-1) }[/math] по распределению при [math]\displaystyle{ d_1,d_2 \to \infty }[/math], где [math]\displaystyle{ \delta(x-1) }[/math] — дельта-функция в единице, то есть распределение случайной величины-константы [math]\displaystyle{ X \equiv 1 }[/math].
Связь с другими распределениями
- Если [math]\displaystyle{ F_{d_1,d_2} \sim \mathrm{F}(d_1,d_2) }[/math], то случайные величины [math]\displaystyle{ d_1 F_{d_1,d_2} }[/math] сходятся по распределению к [math]\displaystyle{ \chi^2(d_1) }[/math] при [math]\displaystyle{ d_2 \to \infty }[/math].
Примечания
- ↑ Johnson N. L., Kotz S., Balakrishnan N. Continuous Univariate Distributions, Volume 2 (Second Edition, Section 27).. — Wiley, 1995. — ISBN 0-471-58494-0.
Ссылки
- Table of critical values of the F-distribution
- Earliest Uses of Some of the Words of Mathematics: entry on F-distribution contains a brief history
- Free calculator for F-testing
Для улучшения этой статьи желательно: |