Метод Ньютона

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить ноль первой производной либо градиента в случае многомерного пространства.

Описание метода

Обоснование

Чтобы численно решить уравнение [math]\displaystyle{ f(x)=0 }[/math] методом простой итерации, его необходимо привести к эквивалентному уравнению: [math]\displaystyle{ x=\varphi(x) }[/math], где [math]\displaystyle{ \varphi }[/math] — сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения [math]\displaystyle{ x^* }[/math] должно выполняться условие [math]\displaystyle{ \varphi'(x^*)=0 }[/math]. Решение данного уравнения ищут в виде [math]\displaystyle{ \varphi(x)=x+\alpha(x)f(x) }[/math], тогда:

[math]\displaystyle{ \varphi'(x^*)=1+\alpha'(x^*)f(x^*)+\alpha(x^*) f'(x^*)=0. }[/math]

В предположении, что точка приближения «достаточно близка» к корню [math]\displaystyle{ \tilde{x} }[/math] и что заданная функция непрерывна [math]\displaystyle{ (f(x^*)\approx f(\tilde{x})=0) }[/math], окончательная формула для [math]\displaystyle{ \alpha(x) }[/math] такова:

[math]\displaystyle{ \alpha(x)=-\frac{1}{f'(x)}. }[/math]

С учётом этого функция [math]\displaystyle{ \varphi(x) }[/math] определяется:

[math]\displaystyle{ \varphi(x)=x-\frac{f(x)}{f'(x)}. }[/math]

При некоторых условиях эта функция в окрестности корня осуществляет сжимающее отображение.

Доказательство

Пусть дана функция вещественного переменного дважды непрерывно дифференцируемая в своей области определения, производная которой нигде не обращается в нуль:

[math]\displaystyle{ \scriptstyle{f(x)\colon\mathbb{X}\to\R,\;f(x)\in\mathrm{C}^2(\mathbb{X});\quad\forall x\in\mathbb{X}\;f'(x)\neq 0.} }[/math]

И необходимо доказать, что функция [math]\displaystyle{ \scriptstyle{\varphi(x)=x-\frac{f(x)}{f'(x)}} }[/math] осуществляет сжимающее отображение вблизи корня уравнения [math]\displaystyle{ \scriptstyle{f(x)=0} }[/math].

В силу непрерывной дифференцируемости функции [math]\displaystyle{ \scriptstyle{f(x)} }[/math] и неравенства нулю её первой производной [math]\displaystyle{ \scriptstyle{\varphi(x)} }[/math] непрерывна.

Производная [math]\displaystyle{ \scriptstyle{\varphi'(x)} }[/math] равна:

[math]\displaystyle{ \scriptstyle{\varphi'(x)=\frac{f(x)f''(x)}{\left(f'(x)\right)^2}.} }[/math]

В условиях, наложенных на [math]\displaystyle{ \scriptstyle{f(x)} }[/math], она также непрерывна. Пусть [math]\displaystyle{ \scriptstyle{\tilde{x}} }[/math] — искомый корень уравнения: [math]\displaystyle{ \scriptstyle{f(\tilde{x})=0} }[/math], следовательно в его окрестности [math]\displaystyle{ \scriptstyle{\varphi'(x)\approx 0} }[/math]:

[math]\displaystyle{ \scriptstyle{\forall\varepsilon\colon 0\lt \varepsilon\lt 1,\;\exist\delta\gt 0\;\forall x\in\mathbb{X}\;|x-\tilde{x}|\lt \delta\colon|\varphi'(x)-0|\lt \varepsilon.} }[/math]

Тогда согласно теореме Лагранжа:

[math]\displaystyle{ \scriptstyle{\forall x_1,\;x_2\in\mathrm{U}_\delta(\tilde{x})\;\exist\xi\in\mathrm{U}_\delta(\tilde{x})\colon|\varphi(x_1)-\varphi(x_2)|=|\varphi'(\xi)| |x_1-x_2|\lt \varepsilon|x_1-x_2|.} }[/math]

В силу того, что [math]\displaystyle{ \scriptstyle{\varphi(\tilde{x})=\tilde{x}} }[/math] в этой же дельта окрестности выполняется:

[math]\displaystyle{ \scriptstyle{\forall x\in U_{\delta}(\tilde{x})\colon\;|\varphi(x)-\tilde{x}|\lt \varepsilon|x-\tilde{x}|.} }[/math]

Таким образом полученная функция [math]\displaystyle{ \scriptstyle{\varphi(x)} }[/math] в окрестности корня [math]\displaystyle{ \scriptstyle{U_\delta(\tilde{x})} }[/math] осуществляет сжимающее отображение.■

В этом случае алгоритм нахождения численного решения уравнения [math]\displaystyle{ f(x)=0 }[/math] сводится к итерационной процедуре вычисления:

[math]\displaystyle{ x_{n+1}=x_{n}-\frac{f(x_n)}{f'(x_n)}. }[/math]

По теореме Банаха последовательность приближений стремится к корню уравнения [math]\displaystyle{ f(x)=0 }[/math].

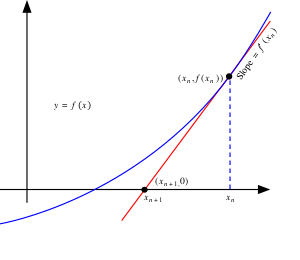
Геометрическая интерпретация

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть 1) вещественнозначная функция [math]\displaystyle{ f(x)\colon(a,\,b)\to\R }[/math] непрерывно дифференцируема на интервале [math]\displaystyle{ (a,\,b) }[/math] ;
2) существует искомая точка [math]\displaystyle{ x^{*}\in (a,\,b) }[/math] : [math]\displaystyle{ f(x^{*})= 0 }[/math] ;
3) существуют [math]\displaystyle{ C \gt 0 }[/math] и [math]\displaystyle{ \delta \gt 0 }[/math] такие, что
[math]\displaystyle{ \vert f'(x) \vert \geqslant C }[/math] для [math]\displaystyle{ x\in(a,\,x^{*}-\delta ] \cup [ x^{*}+\delta,\,b) }[/math]
и [math]\displaystyle{ f'(x)\ne 0 }[/math] для [math]\displaystyle{ x\in(x^{*}-\delta,\, x^{*})\cup(x^{*},\, x^{*}+\delta ) }[/math] ;
4) точка [math]\displaystyle{ x_n \in (a,\,b) }[/math] такова, что [math]\displaystyle{ f(x_n)\ne 0 }[/math] .
Тогда формула итеративного приближения [math]\displaystyle{ x_n }[/math] к [math]\displaystyle{ x^{*} }[/math] может быть выведена из геометрического смысла касательной следующим образом:

[math]\displaystyle{ f'(x_n)=\mathrm{tg}\,\alpha_{n} = \frac{\Delta y}{\Delta x} = \frac{f(x_n)-0}{x_n-x_{n+1}} = \frac{0-f(x_n)}{x_{n+1}-x_n}, }[/math]

где [math]\displaystyle{ \alpha_{n} }[/math] — угол наклона касательной прямой [math]\displaystyle{ y(x)=f(x_n) + (x - x_n) \cdot \mathrm{tg}\,\alpha_{n} }[/math] к графику [math]\displaystyle{ f }[/math] в точке [math]\displaystyle{ (x_n;f(x_n)) }[/math] .

Следовательно (в уравнении касательной прямой полагаем [math]\displaystyle{ y(x_{n+1})=0 }[/math]) искомое выражение для [math]\displaystyle{ x_{n+1} }[/math] имеет вид :

[math]\displaystyle{ x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}. }[/math]

Если [math]\displaystyle{ x_{n+1} \in (a,\,b) }[/math], то это значение можно использовать в качестве следующего приближения к [math]\displaystyle{ x^{*} }[/math] .

Если [math]\displaystyle{ x_{n+1} \notin (a,\,b) }[/math], то имеет место «перелёт» (корень [math]\displaystyle{ x^{*} }[/math] лежит рядом с границей [math]\displaystyle{ (a,\,b) }[/math]). В этом случае надо (воспользовавшись идеей метода половинного деления) заменять [math]\displaystyle{ x_{n+1} }[/math] на [math]\displaystyle{ \frac{x_{n}+x_{n+1}}{2} }[/math] до тех пор, пока точка «не вернётся» в область поиска [math]\displaystyle{ (a,\,b) }[/math] .

Замечания. 1) Наличие непрерывной производной даёт возможность строить непрерывно меняющуюся касательную на всей области поиска решения [math]\displaystyle{ (a,\,b)\; }[/math] .
2) Случаи граничного (в точке [math]\displaystyle{ a }[/math] или в точке [math]\displaystyle{ b }[/math]) расположения искомого решения [math]\displaystyle{ x^{*} }[/math] рассматриваются аналогичным образом.
3) С геометрической точки зрения равенство [math]\displaystyle{ f'(x_n)= 0 }[/math] означает, что касательная прямая к графику [math]\displaystyle{ f }[/math] в точке [math]\displaystyle{ (x_n;f(x_n)) }[/math] - параллельна оси [math]\displaystyle{ OX }[/math] и при [math]\displaystyle{ f(x_n)\ne 0 }[/math] не пересекается с ней в конечной части.
4) Чем больше константа [math]\displaystyle{ C \gt 0 }[/math] и чем меньше константа [math]\displaystyle{ \delta \gt 0 }[/math] из пункта 3 условий, тем для [math]\displaystyle{ x_{n}\in(a,\,x^{*}-\delta ] \cup [ x^{*}+\delta,\,b) }[/math] пересечение касательной к графику [math]\displaystyle{ f }[/math] и оси [math]\displaystyle{ OX }[/math] ближе к точке [math]\displaystyle{ (x^{*};\;0) }[/math] , то есть тем ближе значение [math]\displaystyle{ x_{n+1} }[/math] к искомой [math]\displaystyle{ x^{*}\in (a,\,b) }[/math] .

Итерационный процесс начинается с некоторого начального приближения [math]\displaystyle{ x_0 \in (a,\,b) }[/math] , причём между [math]\displaystyle{ x_0 \in (a,\,b) }[/math] и искомой точкой [math]\displaystyle{ x^{*}\in (a,\,b) }[/math] не должно быть других нулей функции [math]\displaystyle{ f }[/math] , то есть «чем ближе [math]\displaystyle{ x_0 }[/math] к искомому корню [math]\displaystyle{ x^{*} }[/math] , тем лучше». Если предположения о нахождении [math]\displaystyle{ x^{*} }[/math] отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях.

Для предварительно заданных [math]\displaystyle{ \varepsilon_{x} \gt 0 }[/math] , [math]\displaystyle{ \varepsilon_{f} \gt 0 }[/math] итерационный процесс завершается если [math]\displaystyle{ \left \vert \frac{f(x_n)}{f'(x_n)} \right \vert \approx \vert x_{n+1}-x_n \vert \lt \varepsilon_{x} }[/math] и [math]\displaystyle{ \vert f(x_{n+1})\vert \lt \varepsilon_{f} }[/math] .
В частности, для матрицы дисплея [math]\displaystyle{ \varepsilon_{x} }[/math] и [math]\displaystyle{ \varepsilon_{f} }[/math] могут быть рассчитаны, исходя из масштаба отображения графика [math]\displaystyle{ f }[/math] , то есть если [math]\displaystyle{ x_n }[/math] и [math]\displaystyle{ x_{n+1} }[/math] попадают в один вертикальный, а [math]\displaystyle{ f(x_n) }[/math] и [math]\displaystyle{ f(x_{n+1}) }[/math] в один горизонтальный ряд.

Алгоритм

Задается начальное приближение [math]\displaystyle{ x_0 }[/math].
Пока не выполнено условие остановки, в качестве которого можно взять [math]\displaystyle{ |x_{n+1}-x_n|\lt \varepsilon }[/math] или [math]\displaystyle{ |f(x_{n+1})|\lt \varepsilon }[/math] (то есть погрешность в нужных пределах), вычисляют новое приближение: [math]\displaystyle{ x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} }[/math].

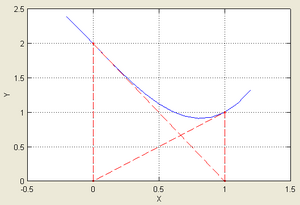
Пример

Иллюстрация применения метода Ньютона к функции [math]\displaystyle{ f(x)=\cos x-x^3 }[/math] с начальным приближением в точке [math]\displaystyle{ x_0=0{,}5 }[/math].
График последовательных приближений.	График сходимости.
Согласно способу практического определения скорость сходимости может быть оценена как тангенс угла наклона графика сходимости, то есть в данном случае равна двум.

Рассмотрим задачу о нахождении положительных [math]\displaystyle{ x }[/math], для которых [math]\displaystyle{ \cos x=x^3 }[/math]. Эта задача может быть представлена как задача нахождения нуля функции [math]\displaystyle{ f(x)=\cos x-x^3 }[/math]. Имеем выражение для производной [math]\displaystyle{ f'(x)=-\sin x-3x^2 }[/math]. Так как [math]\displaystyle{ \cos x\leqslant 1 }[/math] для всех [math]\displaystyle{ x }[/math] и [math]\displaystyle{ x^3\gt 1 }[/math] для [math]\displaystyle{ x\gt 1 }[/math], очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение [math]\displaystyle{ x_0 = 0{,}5 }[/math], тогда:

[math]\displaystyle{ \begin{matrix} x_1 & = & x_0-\dfrac{f(x_0)}{f'(x_0)} & = & 1{,}112\;141\;637\;097, \\ x_2 & = & x_1-\dfrac{f(x_1)}{f'(x_1)} & = & \underline{0{,}}909\;672\;693\;736, \\ x_3 & = & x_2-\dfrac{f(x_2)}{f'(x_2)} & = & \underline{0{,}86}7\;263\;818\;209, \\ x_4 & = & x_3-\dfrac{f(x_3)}{f'(x_3)} & = & \underline{0{,}865\;47}7\;135\;298, \\ x_5 & = & x_4-\dfrac{f(x_4)}{f'(x_4)} & = & \underline{0{,}865\;474\;033\;1}11, \\ x_6 & = & x_5-\dfrac{f(x_5)}{f'(x_5)} & = & \underline{0{,}865\;474\;033\;102}. \end{matrix} }[/math]

Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.

Условия применения

Рассмотрим ряд примеров, указывающих на недостатки метода.

Контрпримеры

Если начальное приближение недостаточно близко к решению, то метод может не сойтись.

Пусть

[math]\displaystyle{ f(x)=x^3-2x+2. }[/math]

Тогда

[math]\displaystyle{ x_{n+1}=x_{n}-\frac{x_n^3-2x_n+2}{3x_n^2-2}. }[/math]

Возьмём ноль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст ноль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.

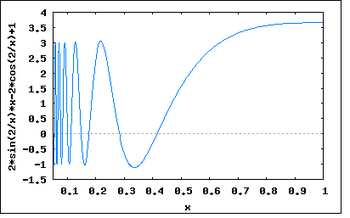
Если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня.

Рассмотрим функцию:

[math]\displaystyle{ f(x)=\begin{cases} 0, & x=0, \\ x+x^2\sin\left(\dfrac{2}{x}\right), & x\neq 0. \end{cases} }[/math]

Тогда [math]\displaystyle{ f'(0)=1 }[/math] и [math]\displaystyle{ f'(x)=1+2x\sin(2/x)-2\cos(2/x) }[/math] всюду, кроме 0.

В окрестности корня производная меняет знак при приближении [math]\displaystyle{ x }[/math] к нулю справа или слева. В то время, как [math]\displaystyle{ f(x)\geqslant x-x^2\gt 0 }[/math] для [math]\displaystyle{ 0\lt x\lt 1 }[/math].

Таким образом [math]\displaystyle{ f(x)/f'(x) }[/math] не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне, [math]\displaystyle{ f }[/math] бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.

Если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена.

Рассмотрим пример:

[math]\displaystyle{ f(x)=x+x^{4/3}. }[/math]

Тогда [math]\displaystyle{ f'(x)=1+(4/3)x^{1/3} }[/math] и [math]\displaystyle{ f''(x)=(4/9)x^{-2/3} }[/math] за исключением [math]\displaystyle{ x=0 }[/math], где она не определена.

На очередном шаге имеем [math]\displaystyle{ x_n }[/math]:

[math]\displaystyle{ x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}=\frac{(1/3)x_n^{4/3}}{(1+(4/3)x_n^{1/3})}. }[/math]

Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и [math]\displaystyle{ f }[/math] бесконечно дифференцируема везде, кроме как в корне.

Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.

Пусть

[math]\displaystyle{ f(x)=x^2. }[/math]

Тогда [math]\displaystyle{ f'(x)=2x }[/math] и следовательно [math]\displaystyle{ x-f(x)/f'(x)=x/2 }[/math]. Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.

Ограничения

Пусть задано уравнение [math]\displaystyle{ f(x)=0 }[/math], где [math]\displaystyle{ f(x)\colon\mathbb{X}\to\R }[/math] и надо найти его решение.

Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).

Теорема Канторовича.

Если существуют такие константы [math]\displaystyle{ A,\;B,\;C }[/math], что:

[math]\displaystyle{ \frac{1}{|f'(x)|}\lt A }[/math] на [math]\displaystyle{ [a,\;b] }[/math], то есть [math]\displaystyle{ f'(x) }[/math] существует и не равна нулю;
[math]\displaystyle{ \left|\frac{f(x)}{f'(x)}\right|\lt B }[/math] на [math]\displaystyle{ [a,\;b] }[/math], то есть [math]\displaystyle{ f(x) }[/math] ограничена;
[math]\displaystyle{ \exist f''(x) }[/math] на [math]\displaystyle{ [a,\;b] }[/math], и [math]\displaystyle{ |f''(x)|\leqslant C\leqslant\frac{1}{2AB} }[/math];

Причём длина рассматриваемого отрезка [math]\displaystyle{ |a-b|\lt \frac{1}{AB}\left(1-\sqrt{1-2ABC}\right) }[/math]. Тогда справедливы следующие утверждения:

на [math]\displaystyle{ [a,\;b] }[/math] существует корень [math]\displaystyle{ x^* }[/math] уравнения [math]\displaystyle{ f(x)=0\colon\exist x^*\in[a,\;b]\colon f(x^*)=0 }[/math];
если [math]\displaystyle{ x_0=\frac{a+b}{2} }[/math], то итерационная последовательность сходится к этому корню: [math]\displaystyle{ \left\{ x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\right\}\to x^* }[/math];
погрешность может быть оценена по формуле [math]\displaystyle{ |x^*-x_n|\leqslant\frac{B}{2^{n-1}}(2ABC)^{2^{n-1}} }[/math].

Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:

[math]\displaystyle{ |x^*-x_n|\leqslant\frac{B}{2^{n-1}}(2ABC)^{2^{n-1}}=\frac{1}{2}\frac{B}{2^{n-2}}\left((2ABC)^{2^{n-2}}\right)^2=\alpha |x^*-x_{n-1}|^2. }[/math]

Тогда ограничения на исходную функцию [math]\displaystyle{ f(x) }[/math] будут выглядеть так:

функция должна быть ограничена;
функция должна быть гладкой, дважды дифференцируемой;
её первая производная [math]\displaystyle{ f'(x) }[/math] равномерно отделена от нуля;
её вторая производная [math]\displaystyle{ f''(x) }[/math] должна быть равномерно ограничена.

Историческая справка

Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» (лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» (лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» (лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения [math]\displaystyle{ x_n }[/math], а последовательность полиномов и в результате получал приближённое решение [math]\displaystyle{ x }[/math].

Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений [math]\displaystyle{ x_n }[/math] вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.

В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» (англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.

Обобщения и модификации

Метод секущих

Родственный метод секущих является «приближённым» методом Ньютона и позволяет не вычислять производную. Значение производной в итерационной формуле заменяется её оценкой по двум предыдущим точкам итераций:

[math]\displaystyle{ f'(x_n) \approx \frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}} }[/math] .

Таким образом, основная формула имеет вид

[math]\displaystyle{ x_{n+1} = x_n - f(x_n) \cdot \frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})} . }[/math]

Этот метод схож с методом Ньютона, но имеет немного меньшую скорость сходимости. Порядок сходимости метода равен золотому сечению — 1,618…

Замечания. 1) Для начала итерационного процесса требуются два различных значения [math]\displaystyle{ x_0 }[/math] и [math]\displaystyle{ x_1 }[/math] .
2) В отличие от «настоящего метода Ньютона» (метода касательных), требующего хранить только [math]\displaystyle{ x_{n} }[/math] (и в ходе вычислений — временно [math]\displaystyle{ f(x_{n}) }[/math] и [math]\displaystyle{ f'(x_{n}) }[/math]), для метода секущих требуется сохранение [math]\displaystyle{ x_{n-1} }[/math] , [math]\displaystyle{ x_{n} }[/math] , [math]\displaystyle{ f(x_{n-1}) }[/math] , [math]\displaystyle{ f(x_{n}) }[/math] .
3) Применяется, если вычисление [math]\displaystyle{ f'(x) }[/math] затруднено (например, требует большого количества машинных ресурсов: времени и/или памяти).

Метод одной касательной

В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.

Формула итераций этого метода имеет вид:

[math]\displaystyle{ x_{n+1}=x_n-\frac{1}{f'(x_0)}f(x_n). }[/math]

Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения [math]\displaystyle{ x_0 }[/math], а затем использовать это значение на каждой последующей итерации:

[math]\displaystyle{ \alpha(x)=\alpha_0=-\dfrac{1}{f'(x_0)}. }[/math]

При таком выборе [math]\displaystyle{ \alpha_0 }[/math] в точке [math]\displaystyle{ x_0 }[/math] выполнено равенство:

[math]\displaystyle{ \varphi'(x_0)=1+\alpha_0f'(x_0)=0, }[/math]

и если отрезок, на котором предполагается наличие корня [math]\displaystyle{ x^* }[/math] и выбрано начальное приближение [math]\displaystyle{ x_0 }[/math], достаточно мал, а производная [math]\displaystyle{ \varphi'(x) }[/math] непрерывна, то значение [math]\displaystyle{ \varphi'(x^*) }[/math] будет не сильно отличаться от [math]\displaystyle{ \varphi'(x_0)=0 }[/math] и, следовательно, график [math]\displaystyle{ y=\varphi(x) }[/math] пройдёт почти горизонтально, пересекая прямую [math]\displaystyle{ y=x }[/math], что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.

Этот метод является частным случаем метода простой итерации. Он имеет линейный порядок сходимости.

Многомерный случай

Обобщим полученный результат на многомерный случай.

Пусть необходимо найти решение системы:

[math]\displaystyle{ \left\{\begin{array}{lcr} f_1(x_1,\;x_2,\;\ldots,\;x_n) & = & 0, \\ \ldots & & \\ f_m(x_1,\;x_2,\;\ldots,\;x_n) & = & 0. \end{array}\right. }[/math]

Выбирая некоторое начальное значение [math]\displaystyle{ \vec{x}^{[0]} }[/math], последовательные приближения [math]\displaystyle{ \vec{x}^{[j+1]} }[/math] находят путём решения систем уравнений:

[math]\displaystyle{ f_i+\sum_{k=1}^n\frac{\partial f_i}{\partial x_k}(x^{[j+1]}_k-x_k^{[j]})=0,\qquad i=1,\;2,\;\ldots,\;m, }[/math]

где [math]\displaystyle{ \vec{x}^{[j]}=(x_1^{[j]},\;x_2^{[j]},\;\ldots,\;x_n^{[j]}),\quad j=0,\;1,\;2,\;\ldots }[/math].

Применительно к задачам оптимизации

Пусть необходимо найти минимум функции многих переменных [math]\displaystyle{ f(\vec{x})\colon\R^n\to\R }[/math]. Эта задача равносильна задаче нахождения нуля градиента [math]\displaystyle{ \nabla f(\vec{x}) }[/math]. Применим изложенный выше метод Ньютона:

[math]\displaystyle{ \nabla f(\vec{x}^{[j]})+H(\vec{x}^{[j]})(\vec{x}^{[j+1]}-\vec{x}^{[j]})=0,\quad j=1,\;2,\;\ldots,\;n, }[/math]

где [math]\displaystyle{ H(\vec{x}) }[/math] — гессиан функции [math]\displaystyle{ f(\vec{x}) }[/math].

В более удобном итеративном виде это выражение выглядит так:

[math]\displaystyle{ \vec{x}^{[j+1]}=\vec{x}^{[j]}-H^{-1}(\vec{x}^{[j]})\nabla f(\vec{x}^{[j]}). }[/math]

Следует отметить, что в случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.

Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.

Метод Ньютона — Рафсона

Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:

[math]\displaystyle{ \vec{x}^{[j+1]}=\vec{x}^{[j]}-\lambda_j H^{-1}(\vec{x}^{[j]})\nabla f(\vec{x}^{[j]}), }[/math]

где [math]\displaystyle{ \lambda_j=\arg\min_\lambda f(\vec{x}^{[j]}-\lambda H^{-1}(\vec{x}^{[j]})\nabla f(\vec{x}^{[j]})). }[/math] Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением [math]\displaystyle{ H(f(\vec{x}^{[0]})) }[/math] и обновляют его лишь раз в [math]\displaystyle{ m }[/math] шагов, либо не обновляют вовсе.

Применительно к задачам о наименьших квадратах

На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:

[math]\displaystyle{ F(\vec{x})=\|\vec{f}(\vec{x})\|=\sum_{i=1}^m f_i^2(\vec{x})=\sum_{i=1}^m (\varphi_i(\vec{x})-\mathcal{F}_i)^2\to\min. }[/math]

Эти задачи отличаются особым видом градиента и матрицы Гессе:

[math]\displaystyle{ \nabla F(\vec{x})=2J^T(\vec{x})\vec{f}(\vec{x}), }[/math]

[math]\displaystyle{ H(\vec{x})=2J^T(\vec{x})J(\vec{x})+2Q(\vec{x}),\qquad Q(\vec{x})=\sum_{i=1}^m f_i(\vec{x})H_i(\vec{x}), }[/math]

где [math]\displaystyle{ J(\vec{x}) }[/math] — матрица Якоби вектор-функции [math]\displaystyle{ \vec{f}(\vec{x}) }[/math], [math]\displaystyle{ H_i(\vec{x}) }[/math] — матрица Гессе для её компоненты [math]\displaystyle{ f_i(\vec{x}) }[/math].

Тогда очередной шаг [math]\displaystyle{ \vec{p} }[/math] определяется из системы:

[math]\displaystyle{ \left[J^T(\vec{x})J(\vec{x})+\sum_{i=1}^m f_i(\vec{x})H_i(\vec{x})\right]\vec{p}=-J^T(\vec{x})\vec{f}(\vec{x}). }[/math]

Метод Гаусса — Ньютона

Метод Гаусса — Ньютона строится на предположении о том, что слагаемое [math]\displaystyle{ J^T(\vec{x})J(\vec{x}) }[/math] доминирует над [math]\displaystyle{ Q(\vec{x}) }[/math]. Это требование не соблюдается, если минимальные невязки велики, то есть если норма [math]\displaystyle{ \|\vec{f}(\vec{x})\| }[/math] сравнима с максимальным собственным значением матрицы [math]\displaystyle{ J^T(\vec{x})J(\vec{x}) }[/math]. В противном случае можно записать:

[math]\displaystyle{ J^T(\vec{x})J(\vec{x})\vec{p}=-J^T(\vec{x})\vec{f}(\vec{x}). }[/math]

Таким образом, когда норма [math]\displaystyle{ \|Q(\vec{x})\| }[/math] близка к нулю, а матрица [math]\displaystyle{ J(\vec{x}) }[/math] имеет полный столбцевой ранг, шаг [math]\displaystyle{ \vec{p} }[/math] мало отличается от ньютоновского (с учётом [math]\displaystyle{ Q(\vec{x}) }[/math]), и метод может достигать квадратичной скорости сходимости, хотя вторые производные и не учитываются. Улучшением метода является алгоритм Левенберга — Марквардта, основанный на эвристических соображениях.

Обобщение на комплексную плоскость

До сих пор в описании метода использовались функции, осуществляющие отображения в пределах множества вещественных значений. Однако метод может быть применён и для нахождения нуля функции комплексной переменной. При этом процедура остаётся неизменной:

[math]\displaystyle{ z_{n+1}=z_n-\frac{f(z_n)}{f'(z_n)}. }[/math]

Особый интерес представляет выбор начального приближения [math]\displaystyle{ z_0 }[/math]. Ввиду того, что функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям, и вполне естественно возникает желание выяснить, какие области обеспечат сходимость к тому или иному корню. Этот вопрос заинтересовал Артура Кэли ещё в 1879 году, однако разрешить его смогли лишь в 70-х годах двадцатого столетия с появлением вычислительной техники. Оказалось, что на пересечениях этих областей (их принято называть областями притяжения) образуются так называемые фракталы — бесконечные самоподобные геометрические фигуры.

Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.

Реализация

Scala

object NewtonMethod {

  val accuracy = 1e-6

  @tailrec
  def method(x0: Double, f: Double => Double, dfdx: Double => Double, e: Double): Double = {
    val x1 = x0 - f(x0) / dfdx(x0)
    if (abs(x1 - x0) < e) x1
    else method(x1, f, dfdx, e)
  }

  def g(C: Double) = (x: Double) => x*x - C

  def dgdx(x: Double) = 2*x

  def sqrt(x: Double) = x match {
    case 0 => 0
    case x if (x < 0) => Double.NaN
    case x if (x > 0) => method(x/2, g(x), dgdx, accuracy) 
  }
}

Python

from math import sin, cos
from typing import Callable
import unittest


def newton(f: Callable[[float], float], f_prime: Callable[[float], float], x0: float, 
	eps: float=1e-7, kmax: int=1e3) -> float:
	"""
	solves f(x) = 0 by Newton's method with precision eps
	:param f: f
	:param f_prime: f'
	:param x0: starting point
	:param eps: precision wanted
	:return: root of f(x) = 0
	"""
	x, x_prev, i = x0, x0 + 2 * eps, 0
	
	while abs(x - x_prev) >= eps and i < kmax:
		x, x_prev, i = x - f(x) / f_prime(x), x, i + 1

	return x


class TestNewton(unittest.TestCase):
	def test_0(self):
		def f(x: float) -> float:
			return x**2 - 20 * sin(x)


		def f_prime(x: float) -> float:
			return 2 * x - 20 * cos(x)


		x0, x_star = 2, 2.7529466338187049383

		self.assertAlmostEqual(newton(f, f_prime, x0), x_star)


if __name__ == '__main__':
	unittest.main()

PHP

<?php
// PHP 5.4
function newtons_method(
	$a = -1, $b = 1, 
	$f = function($x) {
	
		return pow($x, 4) - 1;
	
	},
	$derivative_f = function($x) {

		return 4 * pow($x, 3);
	
	}, $eps = 1E-3) {

        $xa = $a;
        $xb = $b;

        $iteration = 0;

        while (abs($xb) > $eps) {

            $p1 = $f($xa);
            $q1 = $derivative_f($xa);
            $xa -= $p1 / $q1;
            $xb = $p1;
            ++$iteration;

        }

        return $xa;

}

Octave

function res = nt()
  eps = 1e-7;
  x0_1 = [-0.5,0.5];
  max_iter = 500;
  xopt = new(@resh, eps, max_iter);   
  xopt
endfunction
function a = new(f, eps, max_iter)
  x=-1;
  p0=1;
  i=0;
 while (abs(p0)>=eps)
    [p1,q1]=f(x);
    x=x-p1/q1;
   p0=p1;
   i=i+1;
 end
 i
 a=x;
endfunction
function[p,q]= resh(x)   % p= -5*x.^5+4*x.^4-12*x.^3+11*x.^2-2*x+1;
   p=-25*x.^4+16*x.^3-36*x.^2+22*x-2;
   q=-100*x.^3+48*x.^2-72*x+22;
endfunction

Delphi

// вычисляемая функция
function fx(x: Double): Double;
begin
  Result := x * x - 17;
end;

// производная функция от f(x)
function dfx(x: Double): Double;
begin
  Result := 2 * x;
end;

function solve(fx, dfx: TFunc<Double, Double>; x0: Double): Double;
const
  eps = 0.000001;
var
  x1: Double;
begin
  x1 := x0 - fx(x0) / dfx(x0); // первое приближение
  while (Abs(x1-x0) > eps) do begin // пока не достигнута точность 0.000001
    x0 := x1;
    x1 := x1 - fx(x1) / dfx(x1); // последующие приближения
  end;
  Result := x1;
end;

// Вызов
solve(fx, dfx,4);

C++

#include <iostream>
#include <math.h>
using namespace std;

double fx(double x) { return x * x - 17;} // вычисляемая функция
double dfx(double x) { return 2*x;} // производная функции

typedef double(*function)(double x); // задание типа function

double solve(function fx, function dfx, double x0, double eps = 1e-8) {
    double xi = x0; //Текущая точка на i-й иттерации
  while (fabs(fx(xi)) >= eps)  // пока не достигнута точность 0.00000001
    xi = xi - fx(xi) / dfx(xi); // последующие приближения
  return xi;
}

void main () {
    cout << solve(fx, dfx, 4) << endl;
}

C

typedef double (*function)(double x);

double TangentsMethod(function f, function df, double xn, double eps) {
   double x1  = xn - f(xn)/df(xn);
   double x0 = xn;
   while(abs(x0-x1) > eps) {
      x0 = x1;
      x1 = x1 - f(x1)/df(x1);
   }
   return x1;
}

//Выбор начального приближения
xn = MyFunction(A)*My2Derivative(A) > 0 ? B : A;

double MyFunction(double x) { return (pow(x, 5) - x - 0.2); } //Ваша функция
double MyDerivative(double x) { return (5*pow(x, 4) - 1); } //Первая производная
double My2Derivative(double x) { return (20*pow(x, 3)); } //Вторая производная

//Пример вызова функции
double x = TangentsMethod(MyFunction, MyDerivative, xn, 0.1)

Haskell

import Data.List ( iterate' )

main :: IO ()
main = print $ solve (\ x -> x * x - 17) ( * 2) 4

-- Функция solve универсальна для всех вещественных типов значения которых можно сравнивать.
solve = esolve 0.000001

esolve epsilon func deriv x0 = fst . head $ dropWhile pred pairs
  where
    pred (xn, xn1) = (abs $ xn - xn1) > epsilon -- Функция pred определяет достигнута ли необходимая точность.
    next xn = xn - func xn / deriv xn -- Функция next вычисляет новое приближение.
    iters   = iterate' next x0        -- Бесконечный список итераций.
    pairs   = zip iters (tail iters)  -- Бесконечный список пар итераций вида: [(x0, x1), (x1, x2) ..].

Литература

Акулич И. Л. Математическое программирование в примерах и задачах : Учеб. пособие для студентов эконом. спец. вузов. — М. : Высшая школа, 1986. — 319 с. : ил. — ББК 22.1 А44. — УДК 517.8^(G).
Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров : Учеб. пособие. — М. : Высшая школа, 1994. — 544 с. : ил. — ББК 32.97 А62. — УДК 683.1^(G). — ISBN 5-06-000625-5.
Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд. — М. : Лаборатория Базовых Знаний, 2000.
Вавилов С. И. Исаак Ньютон. — М. : Изд. АН СССР, 1945.
Волков Е. А. Численные методы. — М. : Физматлит, 2003.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М. : Мир, 1985.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М. : Наука, 1970. — С. 575—576.
Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — Энергоатомиздат, 1972.
Максимов Ю. А.,Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М. : МИФИ, 1982.
Морозов А. Д. Введение в теорию фракталов. — МИФИ, 2002.

См. также

Ссылки

«Бассейны Ньютона» на сайте fractalworld.xaoc.ru
«Исаак Ньютон» на сайте www.scottish-wetlands.org
«Математические работы Канторовича» на сайте Института математики СО РАН
Hazewinkel, Michiel, ed. (2001), Newton method, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Weisstein, Eric W. Newton's Method (англ.) на сайте Wolfram MathWorld.
Newton’s method, Citizendium.
Mathews, J., The Accelerated and Modified Newton Methods, Course notes.
Wu, X., Roots of Equations, Course notes.

Методы оптимизации
Одномерные	Метод золотого сечения Дихотомия Метод парабол Перебор по сетке Метод равномерного блочного поиска Метод Фибоначчи Троичный поиск Метод Пиявского Метод Стронгина
Нулевого порядка	Метод Гаусса Метод Нелдера — Мида Метод Хука — Дживса Метод Розенброка Метод Пауэлла
Первого порядка	Градиентный спуск Метод Зойтендейка Покоординатный спуск Метод сопряжённых градиентов Квазиньютоновские методы Алгоритм Левенберга — Марквардта
Второго порядка	Метод Ньютона Метод Ньютона — Рафсона Алгоритм Бройдена — Флетчера — Гольдфарба — Шанно (BFGS)
Стохастические	Метод Монте-Карло Имитация отжига Эволюционные алгоритмы Дифференциальная эволюция Муравьиный алгоритм Метод роя частиц Алгоритм пчелиной колонии Метод случайных блужданий
Методы линейного программирования	Симплекс-метод Алгоритм Гомори Метод эллипсоидов Метод потенциалов
Методы нелинейного программирования	Последовательное квадратичное программирование