Окрестность

Для термина «окрестность» см. также другие значения.

На плоскости подмножество [math]\displaystyle{ V }[/math] является окрестностью точки [math]\displaystyle{ p }[/math], если вокруг точки можно нарисовать небольшой диск, который будет целиком содержаться в [math]\displaystyle{ V }[/math].

Прямоугольник не может являться окрестностью своих вершин.

Окре́стность точки — множество, содержащее данную точку и близкие (в каком-либо смысле) к ней. В разных разделах математики это понятие определяется по-разному.

Определения

Математический анализ

Основная статья: ε-окрестность

Пусть [math]\displaystyle{ \varepsilon\gt 0 }[/math] произвольное фиксированное число.

Окрестностью точки [math]\displaystyle{ x_0 }[/math] на числовой прямой (иногда говорят [math]\displaystyle{ \varepsilon }[/math]-окрестностью) называется множество точек, удаленных от [math]\displaystyle{ x_0 }[/math] менее чем на [math]\displaystyle{ \varepsilon }[/math], то есть [math]\displaystyle{ O_\varepsilon(x_0) =\{x: |x-x_0|\lt \varepsilon\} }[/math].

В многомерном случае функцию окрестности выполняет открытый [math]\displaystyle{ \varepsilon }[/math]-шар с центром в точке [math]\displaystyle{ x_0 }[/math].

В банаховом пространстве [math]\displaystyle{ (B,\|\cdot\|) }[/math] окрестностью с центром в точке [math]\displaystyle{ x_0 }[/math] называют множество [math]\displaystyle{ A=\{x\in B:\|x-x_0\|\lt \varepsilon\} }[/math].

В метрическом пространстве [math]\displaystyle{ (M,\rho) }[/math] окрестностью с центром в точке [math]\displaystyle{ y }[/math] называют множество [math]\displaystyle{ A=\{x\in M:\rho(x,y)\lt \varepsilon\} }[/math].

Общая топология

Пусть задано топологическое пространство [math]\displaystyle{ (X,\mathcal{T}) }[/math], где [math]\displaystyle{ X }[/math] — произвольное множество, а [math]\displaystyle{ \mathcal{T} }[/math] — определённая на [math]\displaystyle{ X }[/math] топология.

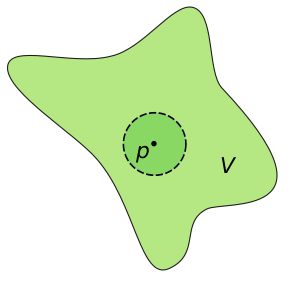
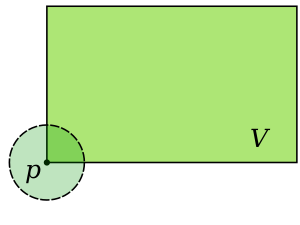
• Множество [math]\displaystyle{ V \subset X }[/math] называется окрестностью точки [math]\displaystyle{ x\in X }[/math], если существует открытое множество [math]\displaystyle{ U\in \mathcal{T} }[/math] такое, что [math]\displaystyle{ x \in U \subset V }[/math].
• Аналогично окрестностью множества [math]\displaystyle{ M \subset X }[/math] называется такое множество [math]\displaystyle{ V \subset X }[/math], что существует открытое множество [math]\displaystyle{ U\in \mathcal{T} }[/math], для которого выполнено [math]\displaystyle{ M \subset U \subset V }[/math].

Замечания

• Приведённые выше определения не требуют, чтобы окрестность [math]\displaystyle{ V }[/math] была открытым множеством, но лишь чтобы она содержала открытое множество [math]\displaystyle{ U }[/math]. Некоторые авторы настаивают на том, что любая окрестность открыта. Тогда окрестностью множества называется любое содержащее его открытое множество. Это не принципиальное для развития дальнейшей топологической теории различие. Однако в каждом случае важно фиксировать терминологию.
• Окрестностью множества точек [math]\displaystyle{ M }[/math] называется такое множество [math]\displaystyle{ V }[/math], что [math]\displaystyle{ V }[/math] есть окрестность любой точки [math]\displaystyle{ x\in M }[/math].

Пример

Пусть дана вещественная прямая со стандартной топологией. Тогда [math]\displaystyle{ (-1,2) }[/math] является открытой окрестностью, а [math]\displaystyle{ [-1,2] }[/math] — замкнутой окрестностью точки [math]\displaystyle{ 0 }[/math].

Вариации и обобщения

Проколотая окрестность

Проколотой окрестностью точки называется окрестность точки, из которой исключена эта точка.

Строго говоря, проколотая окрестность не является окрестностью точки, так как согласно определению окрестности окрестность должна включать и саму точку.

Формальное определение: Множество [math]\displaystyle{ \dot{V} }[/math] называется проколотой окрестностью (вы́колотой окрестностью) точки [math]\displaystyle{ x\in X }[/math], если

[math]\displaystyle{ \dot{V} = V \setminus \{x\}, }[/math]

где [math]\displaystyle{ V }[/math] — окрестность [math]\displaystyle{ x }[/math].

См. также

• Глоссарий общей топологии

Литература

• Математическая Энциклопедия. — М.: Советская Энциклопедия, 1984. — Т. 4.
• У.Рудин. Функциональный анализ. — М.: Мир, 1975.