Алгоритм Гаусса — Ньютона
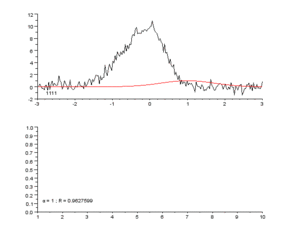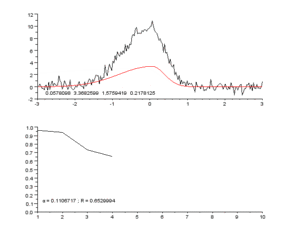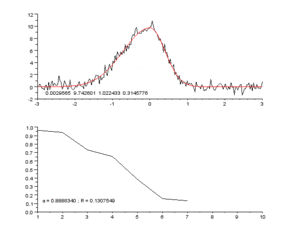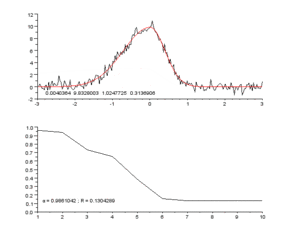
Сверху: необработанные данные и модель.
Снизу: ход нормализованной суммы квадратов ошибок.
Алгоритм Гаусса — Ньютона используется для решения задач нелинейным методом наименьших квадратов[англ.]. Алгоритм является модификацией метода Ньютона для нахождения минимума функции. В отличие от метода Ньютона, алгоритм Гаусса — Ньютона может быть использован только для минимизации суммы квадратов, но его преимущество в том, что метод не требует вычисления вторых производных, что может оказаться существенной трудностью.
Задачи, для которых применяется нелинейный метод наименьших квадратов, возникают, например, при нелинейной регрессии, в которой ищутся параметры модели, которые наиболее соответствуют наблюдаемым величинам.
Метод назван именами математиков Карла Фридриха Гаусса и Исаака Ньютона.
Описание
Если задано m функций r = (r1, …, rm) (часто называемых невязками) от n переменных β = (β1, …, βn), при m ≥ n. Алгоритм Гаусса — Ньютона итеративно находит значения переменных, которые минимизируют сумму квадратов[1]
- [math]\displaystyle{ S(\boldsymbol \beta)= \sum_{i=1}^m r_i^2(\boldsymbol \beta). }[/math]
Начав с некоторого начального приближения [math]\displaystyle{ \boldsymbol \beta^{(0)} }[/math], метод осуществляет итерации
- [math]\displaystyle{ \boldsymbol \beta^{(s+1)} = \boldsymbol \beta^{(s)} - \left(\mathbf{J_r}^\mathsf{T} \mathbf{J_r} \right)^{-1} \mathbf{ J_r} ^\mathsf{T} \mathbf{r}(\boldsymbol \beta^{(s)}) }[/math]
Здесь, если рассматривать r и β как вектор-столбцы, элементы матрицы Якоби равны
- [math]\displaystyle{ (\mathbf{J_r})_{ij} = \frac{\partial r_i (\boldsymbol \beta^{(s)})}{\partial \beta_j} }[/math]
а символ [math]\displaystyle{ ^\mathsf{T} }[/math] означает транспонирование матрицы.
Если m = n, итерации упрощаются до
- [math]\displaystyle{ \boldsymbol \beta^{(s+1)} = \boldsymbol \beta^{(s)} - \left( \mathbf{J_r} \right)^{-1} \mathbf{r}(\boldsymbol \beta^{(s)}) }[/math],
что является прямым обобщением одномерного метода Ньютона.
При аппроксимации данных, где целью является поиск параметров β, таких, что заданная модель функций y = f(x, β) наилучшим образом приближает точки данных (xi, yi), функции ri являются остаточными ошибками[англ.]
- [math]\displaystyle{ r_i(\boldsymbol \beta)= y_i - f(x_i, \boldsymbol \beta). }[/math]
Тогда метод Гаусса — Ньютона можно выразить в терминах якобиана Jf функции f
- [math]\displaystyle{ \boldsymbol \beta^{(s+1)} = \boldsymbol \beta^{(s)} + \left(\mathbf{J_f}^\mathsf{T} \mathbf{J_f} \right)^{-1} \mathbf{ J_f} ^\mathsf{T}\mathbf{r}(\boldsymbol \beta^{(s)}). }[/math]
Заметим, что [math]\displaystyle{ \left(\mathbf{J_f}^\mathsf{T} \mathbf{J_f} \right)^{-1} \mathbf{ J_f} ^\mathsf{T} }[/math] является псевдообратной матрицей к [math]\displaystyle{ \mathbf{J_f} }[/math].
Замечания
Требование m ≥ n в алгоритме необходимо, поскольку в другом случае матрица JrTJr не имеет обратной и нормальные уравнения нельзя решить (по меньшей мере однозначно).
Алгоритм Гаусса — Ньютона можно получить с помощью линейного приближения вектора функций ri. Используя теорему Тейлора, мы можем для каждой итерации записать:
- [math]\displaystyle{ \mathbf{r}(\boldsymbol \beta)\approx \mathbf{r}(\boldsymbol \beta^s)+\mathbf{J_r}(\boldsymbol \beta^s)\Delta }[/math],
где [math]\displaystyle{ \Delta=\boldsymbol \beta-\boldsymbol \beta^s }[/math]. Задача нахождения Δ, минимизирующего сумму квадратов в правой части, т.е.
- [math]\displaystyle{ \mathbf{min}\|\mathbf{r}(\boldsymbol \beta^s)+\mathbf{J_r}(\boldsymbol \beta^s)\Delta\|_2^2 }[/math],
является линейной задачей нахождения наименьших квадратов, которую можно решить явно, что даёт нормальные уравнения.
Нормальные уравнения — это m линейных уравнений по неизвестным приращениям Δ. Уравнения могут быть решены за один шаг, если использовать разложение Холецкого, или, лучше, QR-разложение матрицы Jr. Для больших систем итеративный метод может оказаться более эффективным, если используются такие методы, как метод сопряжённых градиентов. Если имеется линейная зависимость столбцов матрицы Jr, метод итераций завершается неудачей, поскольку JrTJr становится вырожденной.
Пример

В этом примере используется алгоритм Гаусса — Ньютона для построения модели данных путём минимизации суммы квадратов отклонений данных и модели.
В экспериментальной биологии изучение связей между концентрацией субстрата [S] и скоростью реакции в реакции энзимомодуляции, были получены следующие данные.
i 1 2 3 4 5 6 7 [S] 0.038 0.194 0.425 0.626 1.253 2.500 3.740 скорость 0.050 0.127 0.094 0.2122 0.2729 0.2665 0.3317
Нужно найти кривую (функцию-модель) вида
- скорость [math]\displaystyle{ =\frac{V_\text{max}[S]}{K_M+[S]} }[/math],
которая приближает наилучшим образом данные в смысле наименьших квадратов с параметрами [math]\displaystyle{ V_\text{max} }[/math] и [math]\displaystyle{ K_M }[/math], которые следует найти.
Обозначим через [math]\displaystyle{ x_i }[/math] и [math]\displaystyle{ y_i }[/math] значения [S] и скорость из таблицы, [math]\displaystyle{ i=1, \dots, 7 }[/math]. Пусть [math]\displaystyle{ \beta_1=V_\text{max} }[/math] и [math]\displaystyle{ \beta_2=K_M }[/math]. Мы будем искать [math]\displaystyle{ \beta_1 }[/math] и [math]\displaystyle{ \beta_2 }[/math], такие, что сумма квадратов отклонений
- [math]\displaystyle{ r_i = y_i - \frac{\beta_1x_i}{\beta_2+x_i} \; (i=1,\dots, 7) }[/math]
минимальна.
Якобиан [math]\displaystyle{ \mathbf{J_r} }[/math] вектора остатков [math]\displaystyle{ r_i }[/math] по неизвестным [math]\displaystyle{ \beta_j }[/math] — это [math]\displaystyle{ 7\times 2 }[/math] матрица с [math]\displaystyle{ i }[/math]-ой строкой, имеющей элементы
- [math]\displaystyle{ \frac{\partial r_i}{\partial \beta_1}= -\frac{x_i}{\beta_2+x_i},\ \frac{\partial r_i}{\partial \beta_2}= \frac{\beta_1x_i}{\left(\beta_2+x_i\right)^2}. }[/math]
Начав с начального приближения [math]\displaystyle{ \beta_1=0.9 }[/math] и [math]\displaystyle{ \beta_2=0.2 }[/math] после пяти итераций алгоритм Гаусса — Ньютона даёт оптимальные значения [math]\displaystyle{ \hat\beta_1=0.362 }[/math] и [math]\displaystyle{ \hat\beta_2=0.556 }[/math]. Сумма квадратов остатков уменьшается от начального значения 1.445 до 0.00784 к пятой итерации. График справа показывает кривую с оптимальными параметрами.
Сходимость
Можно показать[2], что направление увеличения Δ является направлением спуска[англ.] для S, и, если алгоритм сходится, пределом будет стационарная точка для S. Однако сходимость не гарантируется, даже когда начальная точка близка к решению[англ.], что происходит в методе Ньютона[англ.] или методе BFGS при обычных условиях Фольфе[3].
Скорость сходимости алгоритма Гаусса — Ньютона близка к квадратичной[4]. Алгоритм может сходиться медленнее или не сходиться совсем, если начальное приближение далеко от минимального или если матрица [math]\displaystyle{ \mathbf{J_r^\mathsf{T} J_r} }[/math] плохо обусловлена. Например, представим задачу с [math]\displaystyle{ m=2 }[/math] уравнениями и [math]\displaystyle{ n=1 }[/math] переменной
- [math]\displaystyle{ \begin{align} r_1(\beta) &= \beta + 1 \\ r_2(\beta) &= \lambda \beta^2 + \beta - 1. \end{align} }[/math]
Полученное оптимальное решение — [math]\displaystyle{ \beta = 0 }[/math]. (Настоящий оптимум — [math]\displaystyle{ \beta = -1 }[/math] для [math]\displaystyle{ \lambda = 2 }[/math], поскольку [math]\displaystyle{ S(0) = 1^2 + (-1)^2 = 2 }[/math], в то время как [math]\displaystyle{ S(-1) = 0 }[/math].) Если [math]\displaystyle{ \lambda = 0 }[/math], то задача, фактически, линейна и метод находит решение за одну итерацию. Если |λ| < 1, то метод сходится линейно и ошибка убывает со скоростью |λ| на каждой итерации. Однако, если |λ| > 1, то метод не сходится даже локально[5].
Алгоритм на основе метода Ньютона
Далее предполагается, что алгоритм Гаусса — Ньютона основан на методе Ньютона[англ.] для минимизации функции с помощью аппроксимации. Как следствие, скорость сходимости алгоритма Гаусса — Ньютона может быть квадратична, если выполнены некоторые условия. В общем случае (при более слабых условиях), скорость сходимости может оказаться линейной[6].
Рекуррентное отношение метода Ньютона для минимизации функции S от параметров [math]\displaystyle{ \boldsymbol\beta }[/math]
- [math]\displaystyle{ \boldsymbol\beta^{(s+1)} = \boldsymbol\beta^{(s)} - \mathbf H^{-1} \mathbf g \, }[/math]
где g означает вектор-градиент функции S, а H обозначает гессиан функции S. Поскольку [math]\displaystyle{ S = \sum_{i=1}^m r_i^2 }[/math], градиент задаётся равенством
- [math]\displaystyle{ g_j=2\sum_{i=1}^m r_i\frac{\partial r_i}{\partial \beta_j}. }[/math]
Элементы гессиана вычисляются путём дифференцирования элементов градиента [math]\displaystyle{ g_j }[/math] по [math]\displaystyle{ \beta_k }[/math]
- [math]\displaystyle{ H_{jk}=2\sum_{i=1}^m \left(\frac{\partial r_i}{\partial \beta_j}\frac{\partial r_i}{\partial \beta_k}+r_i\frac{\partial^2 r_i}{\partial \beta_j \partial \beta_k} \right). }[/math]
Метод Гаусса — Ньютона получается путём отбрасывания второй производной (второго члена в выражении). То есть гессиан аппроксимируется
- [math]\displaystyle{ H_{jk}\approx 2\sum_{i=1}^m J_{ij}J_{ik} }[/math],
где [math]\displaystyle{ J_{ij}=\frac{\partial r_i}{\partial \beta_j} }[/math] — элементы якобиана Jr. Градиент и приближённый гессиан можно записать в матричной нотации
- [math]\displaystyle{ \mathbf g=2\mathbf{J}_\mathbf{r}^\mathsf{T}\mathbf{r}, \quad \mathbf{H} \approx 2 \mathbf{J}_\mathbf{r}^\mathsf{T}\mathbf{J_r}.\, }[/math]
Эти выражения подставляются в рекуррентное отношение выше для получения операционных уравнений
- [math]\displaystyle{ \boldsymbol{\beta}^{(s+1)} = \boldsymbol\beta^{(s)}+\Delta;\quad \Delta = -\left( \mathbf{J_r}^\mathsf{T}\mathbf{J_r} \right)^{-1} \mathbf{J_r}^\mathsf{T}\mathbf{r}. }[/math]
Сходимость метода Гаусса — Ньютона в общем случае не гарантирована. Аппроксимация
- [math]\displaystyle{ \left|r_i\frac{\partial^2 r_i}{\partial \beta_j \partial \beta_k}\right| \ll \left|\frac{\partial r_i}{\partial \beta_j}\frac{\partial r_i}{\partial \beta_k}\right| }[/math],
которая должна выполняться для возможности отбрасывания членов со второй производной, может быть получена в двух случаях, для которых сходимость ожидается[7]
- Значения функции [math]\displaystyle{ r_i }[/math] малы по величине, по меньшей мере, рядом с минимумом.
- Функции лишь "слегка" нелинейны, то есть [math]\displaystyle{ \frac{\partial^2 r_i}{\partial \beta_j \partial \beta_k} }[/math] относительно малы по величине.
Улучшенные версии
В методах Гаусса — Ньютона сумма квадратов остатков S может не уменьшаться на каждой итерации. Однако, поскольку Δ направлен в сторону уменьшения функции, если [math]\displaystyle{ S(\boldsymbol \beta^s) }[/math] не является стационарной точкой, выполняется неравенство [math]\displaystyle{ S(\boldsymbol \beta^s+\alpha\Delta) \lt S(\boldsymbol \beta^s) }[/math] для достаточно малых [math]\displaystyle{ \alpha\gt 0 }[/math]. Таким образом, если обнаруживается расходимость, можно использовать долю [math]\displaystyle{ \alpha }[/math] вектора приращения Δ в формуле обновления:
- [math]\displaystyle{ \boldsymbol \beta^{s+1} = \boldsymbol \beta^s+\alpha\ \Delta }[/math].
Другими словами, вектор приращения слишком длинный, но он указывает направление «спуска», так что если пройти лишь часть пути, можно уменьшить значение функции S. Оптимальное значение [math]\displaystyle{ \alpha }[/math] может быть найдено с помощью алгоритма одномерного поиска[англ.], то есть величина [math]\displaystyle{ \alpha }[/math] определяется путём нахождения значения, минимизирующего S с помощью одномерного поиска[англ.] на интервале [math]\displaystyle{ 0\lt \alpha\lt 1 }[/math].
В случаях, когда в направлении вектора приращения оптимальная доля [math]\displaystyle{ \alpha }[/math] близка к нулю, альтернативным методом отработки расходимости является использование алгоритма Левенберга — Марквардта, известного также как «метод доверительных областей»[1]. Нормальные уравнения, модифицированные таким образом, что вектор спуска поворачивается в направлении наискорейшего спуска,
- [math]\displaystyle{ \left(\mathbf{J^TJ+\lambda D}\right)\Delta=-\mathbf{J}^T \mathbf{r} }[/math],
где D — положительная диагональная матрица. Заметим, что если D является единичной матрицей E и [math]\displaystyle{ \lambda\to+\infty }[/math], то [math]\displaystyle{ \lambda\Delta=\lambda\left(\mathbf{J^EJ}+\lambda \mathbf{E}\right)^{-1}\left(-\mathbf{J}^T \mathbf{r}\right)=\left(\mathbf{E}-\mathbf{J^TJ}/ \lambda+\cdots\right)\left(-\mathbf{J}^T \mathbf{r}\right)\to -\mathbf{J}^T \mathbf{r} }[/math]. Таким образом, направление Δ приближает направление отрицательного градиента [math]\displaystyle{ -\mathbf{J}^T \mathbf{r} }[/math].
Так называемый параметр Марквардта [math]\displaystyle{ \lambda }[/math] может также быть оптимизирован путём линейного поиска, но смысла особого нет, поскольку вектор сдвига нужно каждый раз пересчитывать, когда меняется [math]\displaystyle{ \lambda }[/math]. Более эффективная стратегия такая. Если обнаруживается расхождение, увеличиваем параметр Марквардта, пока S убывает. Затем сохраняем значение между итерациями, но уменьшаем его, если возможно, пока не достигнем значения, когда параметр Марквардта не может быть обнулён. Минимизация S тогда становится стандартной минимизацией Гаусса — Ньютона.
Оптимизация больших задач
Для оптимизации большого размера метод Гаусса — Ньютона особенно интересен, поскольку часто (хотя, определённо, не всегда) матрица [math]\displaystyle{ \mathbf{J}_\mathbf{r} }[/math] более разрежена, чем приближённый гессиан [math]\displaystyle{ \mathbf{J}_\mathbf{r}^\mathsf{T}\mathbf{J_r} }[/math]. В таких случаях шаг вычисления сам по себе, обычно, требует применения итеративного приближённого метода, такого как метод сопряжённых градиентов.
Чтобы этот подход работал, необходим как минимум эффективный метод вычисления произведения
- [math]\displaystyle{ \mathbf{J}_\mathbf{r}^\mathsf{T}\mathbf{J_r} \mathbf p }[/math]
для некоторого вектора p. Для хранения разреженной матрицы практично хранить строки матрицы [math]\displaystyle{ \mathbf{J}_\mathbf{r} }[/math] в сжатом виде (т.е. без нулевых элементов), что делает прямое вычисление приведённого выше произведения (ввиду транспозиции) сложным. Однако, если определить ci как строку i матрицы [math]\displaystyle{ \mathbf{J}_\mathbf{r} }[/math], выполняется следующее отношение:
- [math]\displaystyle{ \mathbf{J}_\mathbf{r}^\mathsf{T}\mathbf{J_r} \mathbf p = \sum_i \mathbf c_i (\mathbf c_i \cdot \mathbf p) }[/math]
так что любая строка делает вклад в произведение аддитивно и независимо. Кроме того, это выражение хорошо изучено для применения параллельных вычислений. Заметим, что любая строка ci является градиентом соответствующей невязки ri. При учёте этого обстоятельства вышеприведённая формула подчёркивает факт, что невязки вносят вклад в результат независимо друг от друга.
Связанные алгоритмы
В квазиньютоновских методах, таких как методы Дэвидона, Флетчера и Пауэлла[англ.] или Бройдена — Флетчера — Голдфарба — Шэнно (метод БФГШ) приближение полного гессиана [math]\displaystyle{ \frac{\partial^2 S}{\partial \beta_j \partial\beta_k} }[/math] строится с помощью первых производных [math]\displaystyle{ \frac{\partial r_i}{\partial\beta_j} }[/math] так, что после n уточнений метод по производительности близок к методу Ньютона. Заметим, что квазиньютоновские методы могут минимизировать вещественные функции общего вида, в то время как методы Гаусса — Ньютона, Левенберга — Марквардта и т.д. применимы только к нелинейным задачам наименьших квадратов.
Другой метод решения задач минимизации, использующий только первые производные, это метод градиентного спуска. Однако этот метод не принимает во внимание вторые производные, даже приблизительные. Как следствие, метод крайне малоэффективен для многих функций, особенно в случае сильного взаимного влияния параметров.
Примечания
- ↑ 1,0 1,1 Björck, 1996.
- ↑ Björck, 1996, с. 260.
- ↑ Mascarenhas, 2013, с. 253–276.
- ↑ Björck, 1996, с. 341, 342.
- ↑ Fletcher, 1987, с. 113.
- ↑ Gratton, Lawless, Nichols.
- ↑ Nocedal, Wright, 1999, с. 259-262.
Литература
- A. Björck. Numerical methods for least squares problems. — Philadelphia: SIAM, 1996. — ISBN 0-89871-360-9.
- Roger Fletcher. Practical methods of optimization. — 2nd. — New York: John Wiley & Sons, 1987. — ISBN 978-0-471-91547-8.
- Walter F. Mascarenhas. The divergence of the BFGS and Gauss Newton Methods // Mathematical Programming. — 2013. — Т. 147, вып. 1. — doi:10.1007/s10107-013-0720-6.
- S. Gratton, A.S. Lawless, N.K. Nichols. Approximate Gauss-Newton methods for nonlinear least squares problems. NUMERICAL ANALYSIS REPORT 9/04 (англ.) (недоступная ссылка). The University of Reading (январь 2007). Дата обращения: 20 июля 2017. Архивировано 4 августа 2016 года.
- Jorge Nocedal, Stephen J. Wright. Numerical optimization / Peter Glynn, Stephen M. Robinson. — New York: Springer, 1999. — (Springer Series in Operations Research). — ISBN 0-387-98793-2.
Ссылки
Реализации
- Artelys Knitro. Система для решения нелинейных задач с импленментацией метода Гаусса — Ньютона. Система написана на C и имеет интерфейсы для C++/C#/Java/Python/MATLAB/R.
Для улучшения этой статьи желательно: |