Градиентный спуск
Градиентный спуск, метод градиентного спуска — численный метод нахождения локального минимума или максимума функции с помощью движения вдоль градиента, один из основных численных методов современной оптимизации.
Активно используется в вычислительной математике не только для непосредственного решения задач оптимизации (минимизации), но и для задач, которые могут быть переписаны на языке оптимизации (решение нелинейных уравнений, поиск равновесий, обратные задачи и т. д.). Метод градиентного спуска можно использовать для задач оптимизации в бесконечномерных пространствах, например, для численного решения задач оптимального управления.
Особенно большой интерес к градиентным методам в последние годы связан с тем, что градиентные спуски и их стохастические / рандомизированные варианты лежат в основе почти всех современных алгоритмов обучения, разрабатываемых в анализе данных.
Описание
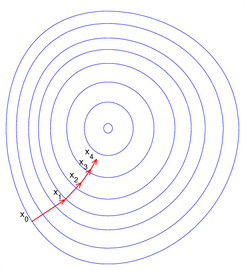
Пусть целевая функция имеет вид:
- [math]\displaystyle{ F(\vec{x}):\;\mathbb{X}\to\mathbb{R} }[/math].
И задача оптимизации задана следующим образом:
- [math]\displaystyle{ F(\vec{x})\to\min_{\vec{x}\in\mathbb{X}} }[/math]
В случае, когда требуется найти максимум, вместо [math]\displaystyle{ F(\vec{x}) }[/math] используется [math]\displaystyle{ -F(\vec{x}) }[/math]
Основная идея метода заключается в том, чтобы идти в направлении наискорейшего спуска, а это направление задаётся антиградиентом [math]\displaystyle{ -\nabla F }[/math]:
- [math]\displaystyle{ \vec{x}^{[j+1]}=\vec{x}^{[j]}-\lambda^{[j]}\nabla F\left(\vec{x}^{[j]}\right) }[/math]
где [math]\displaystyle{ \lambda^{[j]} }[/math]задает скорость градиентного спуска и может быть выбрана
- постоянной (в этом случае метод может расходиться);
- убывающей в процессе градиентного спуска;
- гарантирующей наискорейший спуск:
- Для поиска минимума [math]\displaystyle{ F\left(\vec{x}\right) }[/math] получаем [math]\displaystyle{ \lambda^{[j]} =\mathrm{argmin}_{\lambda} F\left(\vec{x}^{[j+1]}\right) = \mathrm{argmin}_{\lambda} \,F\left(\vec{x}^{[j]}-\lambda\nabla F\left(\vec{x}^{[j]}\right)\right) }[/math]
- Для поиска максимума [math]\displaystyle{ F\left(\vec{x}\right) }[/math] получаем [math]\displaystyle{ \lambda^{[j]} =\mathrm{argmax}_{\lambda} F\left(\vec{x}^{[j+1]}\right) = \mathrm{argmax}_{\lambda} \,F\left(\vec{x}^{[j]}+\lambda\nabla F\left(\vec{x}^{[j]}\right)\right) }[/math]
Алгоритм
- Задают начальное приближение и точность расчёта [math]\displaystyle{ \vec{x}^0, \varepsilon }[/math]
- Рассчитывают [math]\displaystyle{ \vec{x}^{[j+1]}=\vec{x}^{[j]}-\lambda^{[j]}\nabla F\left(\vec{x}^{[j]}\right) }[/math], где [math]\displaystyle{ \lambda^{[j]}=\mathrm{argmin}_{\lambda} \,F\left(\vec{x}^{[j]}-\lambda\nabla F\left(\vec{x}^{[j]}\right)\right) }[/math]
- Проверяют условие остановки:
- Если [math]\displaystyle{ \left|\vec{x}^{[j+1]}-\vec{x}^{[j]}\right|\gt \varepsilon }[/math], [math]\displaystyle{ \left|F\left(\vec{x}^{[j+1]}\right)-F\left(\vec{x}^{[j]}\right)\right|\gt \varepsilon }[/math] или [math]\displaystyle{ \left\| \nabla F\left(\vec{x}^{[j+1]}\right) \right\| \gt \varepsilon }[/math] (выбирают одно из условий), то [math]\displaystyle{ j=j+1 }[/math] и переход к шагу 2.
- Иначе [math]\displaystyle{ \vec{x}=\vec{x}^{[j+1]} }[/math] и останов.
Соотношение Канторовича
Для квадратичной функции вида [math]\displaystyle{ \frac{x^T \Gamma x }{2} + c^T x, \Gamma^T=\Gamma }[/math] метод наискорейшего градиентного поиска сходится из любой начальной точки [math]\displaystyle{ x_0 }[/math] со скоростью геометрической прогрессии (линейно) со знаменателем, не превосходящим значение [math]\displaystyle{ q }[/math]. При этом справедливы следующие оценки:
- [math]\displaystyle{ \exists a=a(x_0), T\gt 0: 0 \le a \le q = \frac{\left ( \lambda_{min} / \lambda_{max} - 1 \right )^2}{\left ( \lambda_{min} / \lambda_{max} + 1 \right )^2} }[/math],
- [math]\displaystyle{ f(x_k) - f(x^*) \le a^k (f(x_0)-f(x^*)) }[/math],
- [math]\displaystyle{ \|x_k - x^* \| \le T a^{k/2} \| x_0 - x^* \| }[/math],
где [math]\displaystyle{ \lambda_{min} }[/math] и [math]\displaystyle{ \lambda_{max} }[/math] — минимальное и максимальное собственные числа матрицы вторых производных [math]\displaystyle{ \nabla^2 f(x) = \Gamma }[/math].
Таким образом, поскольку функция близка в малом к своей квадратичной аппроксимации, скорость сходимости, в окрестности точки минимума, зависит от отношения собственных чисел. Чем больше это отношение, тем хуже сходимость метода.
Пример
Применим градиентный метод к функции [math]\displaystyle{ F(x,y)=\sin\left(\frac{1}{2} x^2 - \frac{1}{4} y^2 + 3 \right) \cos(2 x+1-e^y) }[/math]. Тогда последовательные приближения будут выглядеть так:
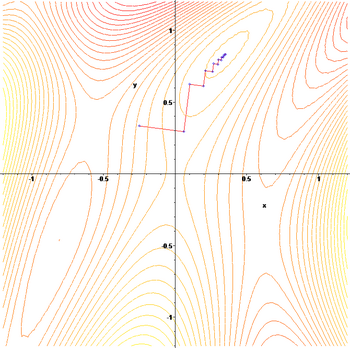
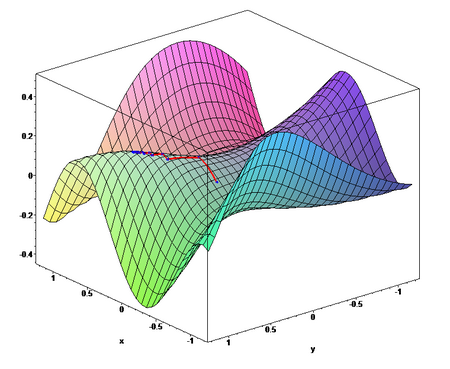
Это типичный пример овражной функции. Градиентный метод «прыгает» с одного склона оврага на другой и обратно, иногда почти не двигаясь в нужном направлении, что существенно замедляет сходимость. Другим примером тестовой овражной функции является функция Розенброка.
Усовершенствования, модификации
Для минимизации функции в направлении градиента используются методы одномерной оптимизации, например, метод золотого сечения. Также можно искать не наилучшую точку в направлении градиента, а какую-либо лучше текущей.
Метод градиентного спуска наиболее простой в реализации из всех методов локальной оптимизации. Имеет довольно слабые условия сходимости, но при этом скорость сходимости достаточно мала (линейна). Шаг градиентного метода часто используется как часть других методов оптимизации, например, метод Флетчера — Ривса.
Метод градиентного спуска оказывается очень медленным при движении по оврагу, причём при увеличении числа переменных целевой функции такое поведение метода становится типичным. Для борьбы с этим явлением используется метод оврагов, суть которого очень проста. Сделав два шага градиентного спуска и получив три точки, третий шаг следует сделать в направлении вектора, соединяющего первую и третью точку, вдоль дна оврага.
Для функций, близких к квадратичным, эффективным является метод сопряжённых градиентов.
Применение в искусственных нейронных сетях
Метод градиентного спуска с некоторой модификацией широко применяется для обучения перцептрона и в теории искусственных нейронных сетей известен как метод обратного распространения ошибки. При обучении нейросети типа «персептрон» требуется изменять весовые коэффициенты сети так, чтобы минимизировать среднюю ошибку на выходе нейронной сети при подаче на вход последовательности обучающих входных данных. Формально, чтобы сделать всего один шаг по методу градиентного спуска (сделать всего одно изменение параметров сети), необходимо подать на вход сети последовательно абсолютно весь набор обучающих данных, для каждого объекта обучающих данных вычислить ошибку и рассчитать необходимую коррекцию коэффициентов сети (но не делать эту коррекцию), и уже после подачи всех данных рассчитать сумму в корректировке каждого коэффициента сети (сумма градиентов) и произвести коррекцию коэффициентов «на один шаг». Очевидно, что при большом наборе обучающих данных алгоритм будет работать крайне медленно, поэтому на практике часто производят корректировку коэффициентов сети после каждого элемента обучения, где значение градиента аппроксимируются градиентом функции стоимости, вычисленном только на одном элементе обучения. Такой метод называют стохастическим градиентным спуском или оперативным градиентным спуском. Стохастический градиентный спуск является одной из форм стохастического приближения. Теория стохастических приближений даёт условия сходимости метода стохастического градиентного спуска.
Ссылки
- J. Mathews. Module for Steepest Descent or Gradient Method.
- Метафорическая интерактивная демонстрация метода Наискорейший Пью
Литература
- Поляк Б. Т. Введение в оптимизацию. — М.: Наука. Главная редакция физико-математической литературы, 1983. — 384 с.
- Нестеров Ю. Е. Методы выпуклой оптимизации. — М.: Издательство МЦНМО, 2010. — 281 с.
- Гасников А. В. Современные численные методы оптимизации. Метод универсального градиентного спуска : учебное пособие. — М.: МФТИ, 2018. — 291 с. — ISBN 978-5-7417-0667-1.
- Акулич И. Л. Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986. — С. 298-310.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация = Practical Optimization. — М.: Мир, 1985.
- Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
- Максимов Ю. А., Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
- Максимов Ю. А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
- Городецкий С. Ю., Гришагин В. А. Нелинейное программирование и многоэкстремальная оптимизация. — Нижний Новгород: Издательство Нижегородского Университета, 2007. — С. 357-363.