Метод эллипсоидов
Метод эллипсоидов — алгоритм нахождения точки, лежащей в пересечении выпуклых множеств. Разработан А. С. Немировским и доведён до алгоритмической реализации Л. Г. Хачияном в ВЦ АН СССР.
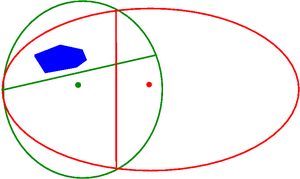
Описание алгоритма
В начале выбирается большой шар, содержащий пересечение выпуклых множеств. Способ построения этого шара зависит от задачи. Далее на каждом шаге имеется эллипсоид, заданный центром [math]\displaystyle{ v }[/math] и векторами [math]\displaystyle{ v_1, v_2, \dots, v_n \in \mathbb{R}^n }[/math]. Эллипсоиду принадлежат точки [math]\displaystyle{ v+c_1v_1+c_2v_2+\cdots+c_nv_n }[/math] для которых [math]\displaystyle{ c_1^2+c_2^2+\cdots+c_n^2\leqslant 1 }[/math]. Отметим, что один и тот же эллипсоид можно задать несколькими способами. Если центр этого эллипсоида принадлежит всем выпуклым множествам, то искомая точка найдена. Иначе существует гиперплоскость [math]\displaystyle{ \pi }[/math], проходящая через точку [math]\displaystyle{ v }[/math], такая, что одно из множеств целиком лежит по одну сторону от неё. Тогда можно перейти от исходного базиса [math]\displaystyle{ v_i }[/math] к другому базису [math]\displaystyle{ \tau, w_2, \dots w_n }[/math] такому, что [math]\displaystyle{ w_i }[/math] параллельны [math]\displaystyle{ \pi }[/math], а [math]\displaystyle{ \tau }[/math] направлен в сторону множества. Положим теперь [math]\displaystyle{ v'=v+\frac{\tau}{n+1} }[/math], [math]\displaystyle{ v'_1=\frac{n\tau}{n+1} }[/math], [math]\displaystyle{ v'_i=w_i\frac{n}{\sqrt{n^2-1}} }[/math] при [math]\displaystyle{ i\ge 2 }[/math]. Этот новый эллипсоид содержит половину старого и имеет меньший объём. Таким образом, объём эллипсоида уменьшается экспоненциально с ростом числа шагов и искомая точка будет найдена за [math]\displaystyle{ O(n^2\log(V_1/V_2)) }[/math] шагов, где [math]\displaystyle{ V_1 }[/math] — объем исходного шара, а [math]\displaystyle{ V_2 }[/math] — объем области пересечения. Общее время работы алгоритма получается равным [math]\displaystyle{ O(Ntn^2\log(V_1/V_2)) }[/math], где [math]\displaystyle{ N }[/math] — число множеств, [math]\displaystyle{ t }[/math] — время проверки принадлежности точки множеству.
Применение к задаче линейного программирования
Если в задаче линейного программирования удалось построить шар, содержащий искомое решение, то она может быть решена методом эллипсоидов. Для этого вначале находим какую-нибудь точку [math]\displaystyle{ u }[/math] внутри шара, удовлетворяющую ограничениям задачи. Проводим через неё гиперплоскость [math]\displaystyle{ f(x)\lt f(u) }[/math], где [math]\displaystyle{ f }[/math] — целевая функция, и находим точку в пересечении исходных и новой гиперплоскостей (начиная с текущего эллипсоида). С новой найденной точкой проделываем то же самое. Процесс сходится к оптимальному решению с экспоненциальной скоростью (поскольку с этой скоростью убывает объём эллипсоида).
Эффективность метода
Полиномиальный алгоритм теоретически мог бы стать новым стандартом, однако, на практике алгоритм Хачияна применять следует с осторожностью: существуют задачи размером в 50 переменных, для которых требуются более 24 тысяч итераций метода Хачияна, количество же существенно более простых итераций симплекс-метода в таких случаях исчисляется сотнями или даже десятками [1][2]. Однако есть примеры задач, для которых алгоритмы этого класса работают в сотни раз эффективнее стандартных реализаций симплекс-метода.
Примечания
- ↑ Николенко, 2005.
- ↑ Схрейвер, 1991, с. 264.
Литература
- С.А. Ашманов. Линейное программирование. — М.: Главная редакция физико-математической литературы, 1981. — С. 288-289.
- А. Схрейвер. Теория линейного и целочисленного программирования, т1. — М.: «Мир», 1991. — ISBN 5-03-002754-8.
- С. Николенко. Теория и практика сложности // Компьютерра. — М.: ООО Журнал «Компьютерра», 2005. — Вып. 31.
В статье не хватает ссылок на источники (см. также рекомендации по поиску). |